1. _{Звичайні сили інерції чи вихрове електричне поле.}

2. Частоти Лармора.

3. Вихрове електричне поле

_{Звичайні сили інерції чи вихрове електричне поле}

_{Звернемося тепер до другого доданка початкової формули яке являє собою звичайну силу інерції, зв'язану зі зміною поступальної чи швидкості швидкості обертання:}

(1.9.1)

_{Перша частина цієї сили являє собою найпростішу силу інерції, зв'язану зі зміною швидкості поступального руху. Її механічний приклад очевидний - при чи прискоренні уповільненні візка, що рухається, лежачий на ній брусок зміщається чи назад уперед.}

_{Польове втілення цієї сили також легко продемонструвати (малюнок 1.9.1). Зміна напруги на кінцях проводу в концепції польового середовища означає чи прискорення уповільнення єдиної польової оболонки провідника, що і надає руху електронам. Для електронів такі зміни аналогічні зміні швидкості візка в механіку. При уповільненні польової оболонки, тобто при вимиканні струму, електрони по інерції намагаються продовжити рух і як би відтворити зникаючий струм. При прискоренні польової оболонки, чи при включенні струм}

_{а, усі відбувається з точністю навпаки, тому що в цьому випадку електрони пручаються виникненню руху. Це явище зветься самоіндукції і також відомо у фізику вже дуже багато років!}

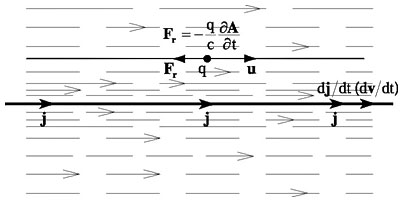
_{Малюнок 1.9.1. Частина вихрового електричного полючи зв'язана з дією звичайної сили інерції в польовому середовищі, обумовленим перемінною швидкістю її руху.}

_{Правило Ленца, відповідно до якого ЭДС індукції завжди протилежна зміні величини струму, є ні чим іншим, як продовженням принципу про сили інерції, що завжди перешкоджають зміні характеру руху об'єктів!}

_{Величина сили електромагнітної індукції виходить з величини сили інерції:}

(1.9.2)

де Er являє собою деяке ефективне електричне поле, чисельно рівне дії сили інерції. Обчислення ротора від обох частин цього вираження дає:

(1.9.3)

Операція ротора береться по координатах крапки реєстрації, отже, v при цьому вважається постійною. У результаті

(1.9.4)

У цій формулі ми довідаємося вираження для вихрового електричного полючи:

(1.9.5) де B як і раніше:

(1.9.6.)

_{Другий доданок у звичайній силі інерції має аналогічну суть. Розходження складається лише в тім, що замість лінійної швидкості ми розглядаємо кутову. Візьмемо знову лише ту частину кутової швидкості ω = -ω, що залежить від швидкості джерела.}

Вираження для ротора ефективного полючи Er:

Ротор векторного добутку по відомій формулі аналізу дорівнює:

_{з огляду на, що похідні беруться по координатах крапки реєстрації при постійної ω.}

_{Перший доданок у правій частині цієї формули:}

_{Ротор векторного добутку по відомій формулі аналізу дорівнює:}

(1.9.9.)

(1.9.10)

_{Другий доданок у правій частині вираження (1.9.9) дорівнює нулю, тому що вектор ω ортогонален R, а даний доданок являє собою похідну від одного з цих векторів по напрямку другого.}

_{У такий спосіб}

(1.9.11)

(1.9.12)

(1.9.13)

_{Ми знову одержали знайому формулу для вихрового електричного полючи!Найбільш цікавим виявляється вираження для вектора B. Його варто небагато перетворити:}

(1.9.14)

(1.9.15)

_{Це значення кутової швидкості вже давно було відзначено фізиками як особливе. Воно зветься частоти Лармора і володіє тим примітною властивістю, що поводження часток у магнітному полі з напруженістю B цілком аналогічно їх поводженню в системі відліку, що обертається з зазначеною частотою! Тепер нам до кінця зрозуміло чому, адже саме магнітне поле саме і є сила інерції в польовому середовищі, що обертається з цією швидкістю!}

_{Механізм дії даної сили інерції найбільш простий (малюнок 1.9.2). Нехай магнітне поле створюється петлею зі струмом. Польове середовище усередині цього кільця, як уже відзначалося вище, буде подібна воді, що обертається в лійці, чи ж крутиться диску. Зміна кутової швидкості обертання польового середовища може бути викликано, наприклад, зміною струму в кільці.}

_{Малюнок 1.9.2. Інша частина вихрового електричного полючи зв'язана з дією звичайної сили інерції в польовому середовищі, обумовленим перемінною швидкістю її обертання.}

_{У цьому випадку на будь-яку спробну частку буде діяти тангенціально спрямована сила інерції. Вона подібна тим У цьому випадку на будь-яку спробну частку буде діяти тангенціально спрямована сила інерції. Вона подібна тим силам, що виникають при зміні кутової швидкості обертання диска. На всі тіла, що знаходяться на диску, по дотичній до окружності діє сила по напрямку руху, якщо диск гальмує, і проти напрямку руху, якщо диск розганяється. От чому при зміні струму в кільці виникає сила, що прагне обертати спробну частку по окружності, і циркуляція цієї сили по замкнутому контурі відмінна від нуля! Якщо в це польове середовище ми помістимо інше кільце, то при зміні кутової швидкості обертання польового середовища - величини магнітного полючи - у другому кільці з'явиться ЭДС і піде струм. Природа цього струму дуже схожа на природу обертання грузлої рідини поблизу від диска, що крутиться.}

_{Вихрове електричне поле не є фундаментальним фізичним полем. Його природа складається в дії звичайних сил інерції, зв'язаних зі зміною швидкості чи руху швидкості обертання польового середовища.}

Л.С.Жданов. Підручник по фізиці для середніх спеціальних навчальних закладів. § 26.7 – 29.8 стор. 299 - 300.

Питання для самоперевірки.

1. _{Як визначити сили інерції вихрового електричного струму?}

2. _{Основна формула за якою визначається частота Лармора.}

3. _{Основна відзнака вихрового електричного поля.}

_{3.7 Тема 3.}

Магнітне потокозчеплення. Зв′язок вихрового електричного поля з магнітним

_План.

1. _{Магнітний потік і потокозчеплення .}

2. _{Магнітна індукція.}

_{3. Лінії вектора магнітної індукції .}

_{4. Магнітний потік, що проходить через будь-яку замкнуту поверхню.}

_{5. Зв´язок вихрового електричного полю з магнітним.}

_{Магнітний потік і потокозчеплення ..}

_{У просторі, що оточує провідники, по яких протікає електричний струм, а також навколишні постійні магніти, існує ряд фізичних явищ, що виявляються у виникненні ЭДС у провідниках, що рухаються, механічному впливі на постійні магніти і провідники зі струмом, що знаходяться в цьому просторі й ін.}

_{Простір, у якому відбуваються ці явища, називається магнітним полем.}

_{Для визначення кількісних характеристик магнітного полючи можна використовувати будь-який його прояв, однак звичайно використовують явище електромагнітної індукції і механічний вплив з боку полючи.}

_{Явище електромагнітної індукції полягає у виникненні ЭДС провідниках. Причому, умови, при яких вона виникає можуть бути всілякими . Це може відбуватися, наприклад, при русі провідника в однорідному магнітному чи полі в нерухомому провіднику, що знаходиться в перемінному магнітному полі.}

_{Визначити основні співвідношення для цього явищі можна за допомогою пристрою показаного на мал. 1. Воно являє собою тонкий провідник, вигнутий у виді кільця K і підключений гнучким крученим проводом до балістичного гальванометра G. Відхилення стрілки балістичного гальванометра пропорційно кількості зарядів q, що протекли через нього.}

_{Якщо центр кільця K поміщати в різні крапки простору навколо постійного магніту, а потім швидко відносити на значну відстань, то гальванометр буде фіксувати різні значення q. Відстань, на яке потрібно видаляти кільце теоретично повинне бути нескінченним для того, щоб усі прояви полючи були зведені до нуля.}

_{При повторенні досвіду з однієї і тієї ж крапки простору ми будемо одержувати однакові значення q, але якщо змінити опір ланцюга r, по якій протікають заряди, то величина q зміниться назад пропорційно r. Звідси можна зробити висновок, що}

_{кожна крапка простору навколо постійного магніту має деяку властивість, що визначає кількість зарядів q, що протікають через гальванометр при видаленні кільця K на значну відстань від магніту. Позначимо цю властивість символом Ф и назвемо його магнітним потоком, залишаючи поки значеннєве обґрунтування терміна. Тоді можна записати відзначену вище зв'язок у виді вираження:}

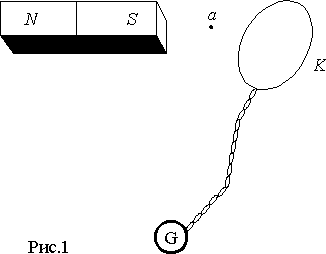
q = Ф/r или Ф = qr

_{Повторимо досвіди з кільцем в одній і тій же крапці простору постійного магніту, наприклад, у крапці a мал. 1, при незмінному опорі ланцюга і положенні площини кільця. При цьому будемо поступово змінювати площа кільця. Якщо площа кільця досить мала, то зміни кількості зарядів q будуть у точності пропорційні зміні площі кільця s. Але кількість зарядів пропорційно величині магнітного потоку, тому і зміни магнітного потоку пропорційні зміні площі, тобто}

 Ф = B_as чи, переходячи до нескінченно малих, dФ = B_ads , (2)

_{де величина Ba не залежить від розмірів кільця і визначається тільки положенням крапки a, отже, вона характеризує магнітне поле в даній крапці простору і називається магнітною індукцією.}

_{Якщо досвіди в крапці a продовжити, змінюючи положення площини кільця в початковий момент, то можна установити, що існує таке його положення, при якому кількість зарядів буде максимальним і усяким відхиленням від цього положення буде приводити до їхнього зменшення пропорційно косинусу кута відхилення. Включаючи цю умову у вираження (2) одержимо}

dФ = B_acos ds, (3)

_{де β - кут між напрямком нормалі до площини спробного витка і напрямком, при якому кількість зарядів, що протікають через виток максимально.}

_{В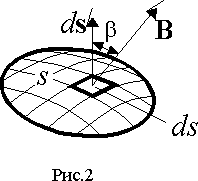 ираження (3) показує, що магнітна індукція B є векторною величиною і її напрямком збігається з напрямком нормалі до площини спробного витка, при якому кількість зарядів, що протікають через виток при його видаленні на значну відстань, максимально.}

_{Досвіди зі спробним витком (кільцем) можна проводити також і в просторі котушки, підключеної до джерела постійного струму. При цьому замість видалення витка можна просто виключати струм, тому що в обох випадках магнітний потік буде зменшуватися до нуля Якщо в просторі виділити деяку поверхню s, то магнітний потік через цю поверхню визначиться з вираження (3) у виді}

_{де ds - вектор чисельно рівний поверхні ds і мающий напрямок нормалі до цієї поверхні (рис 2.).}

_{З вираження (4) випливає, що магнітний потік є потоком вектора магнітної індукції через деяку поверхню. Одиницею магнітного потоку є Вебер (1 Вб = 1 В с).}

_{Якщо поверхня ds нормальна до вектора B, то cos = 1 і з вираження (3)}

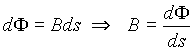(5)

_{т.е. магнітна індукція є щільністю магнітного потоку в даній крапці полючи. Одиницею магнітної індукції є тесла (1 Тл = 1 Вб/м}²_).

_{Повертаючи до отриманого раніше вираженню (1), можна кількісно визначити магнітний потік через деяку поверхню як добуток величини заряду, що протікає ч ерез провідник сполучений із границею цієї поверхні при повному зникненні магнітного полючи, на опір електричного ланцюга, по якій протікають ці заряди.}

_{В описаних вище досвідах зі спробним витком (кільцем), він віддалявся на таку відстань, при якому зникали всякі прояви магнітного полючи. Але можна просто переміщати цей виток у межах полючи і при цьому в ньому також будуть переміщатися електричні заряди.}

_{Перейдемо у вираженні (1) до збільшень}

Ф +  Ф = r(q   q)   Ф =  r q   q =   Ф/r (6)

де Δ Ф и Δ q - збільшення потоку і кількості зарядів. Різні знаки збільшень порозуміваються тим, що позитивний заряд у досвідах з видаленням витка відповідав зникненню полючи, тобто негативному збільшенню магнітного потоку.

_{За допомогою спробного витка можна досліджувати весь простір навколо чи магніту котушки зі струмом і побудувати лінії, напрямок дотичних до яких у кожній крапці буде відповідати напрямку вектора магнітної індукції B (мал. 3)}

_{Ці лінії називаються лініями вектора магнітної чи індукції магнітними лініями.}

_{Простір магнітного полючи можна думкою розділити трубчастими поверхнями, утвореними магнітними лініями, причому, поверхні можна вибрати таким чином, щоб магнітний потік усередині кожної такої поверхні (трубки) чисельно був дорівнює одиниці і зобразити графічно осьові лінії цих трубок. Такі трубки називають одиничними, а лінії їхніх осей - одиничними магнітними лініями. Картина магнітного полючи зображена за допомогою одиничних ліній дає не тільки про якісне, але і кількісне представлення про нього, тому що при цьому величина вектора магнітної індукції виявляється рівної кількості ліній, що проходять через одиницю поверхні, нормальної вектору B, а кількість ліній, що проходять через будь-яку поверхню дорівнює значенню магнітного потоку.}

_{Магнітні лінії безупинні і цей принцип можна математично представити у виді}

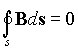
_{т.е. магнітний потік, що проходить через будь-яку замкнуту поверхню дорівнює нулю.}

_{________________________________________}

_{Вираження (4) справедливо для поверхні s будь-якої форми. Якщо розглядати магнітний потік минаючий через поверхню, утворену витками циліндричної котушки (мал. 4), то її можна розділити на поверхні, утворені окремими витками, тобто s=s1+s2+...+s8. Причому через поверхні різних витків у загальному випадку будуть проходити різні магнітні потоки. Так на мал. 4, через поверхні центральних витків котушки проходять вісім одиничних магнітних ліній, а через поверхні крайніх витків тільки чотири.}

_{Для того, щоб визначити повний магнітний потік, що проходить через поверхню усіх витків, потрібно скласти потоки, що проходять через поверхні окремих витків, чи, інакше кажучи, що зчіплюються з окремими витками.}

_{Наприклад, магнітні потоки, що зчіплюються з чотирма верхніми витками котушки мал. 4, будуть рівні: Ф1=4; Ф2=4; Ф3=6; Ф4=8.}

_{Загальний магнітний потік, що зчіплюється з усіма витками котушки, називається потокозчепленням і чисельно дорівнює сумі потоків, що зчіплюються з окремими витками, тобто = 2(Ф1+ Ф2+ Ф3+ Ф4) = 48}

_{Часто реальний розподіл потокозчеплення. по витках котушки невідомо, але його можна прийняти рівномірним і однакової для усіх витків, якщо реальну котушку}

_{замінити еквівалентної з іншим числом витків wэ, зберігаючи при цьому величину потокозчеплення}  = w_эФ_{m , де Фm - потік, що зчіплюється з внутрішніми витками котушки, а wэ - еквівалентне чи ефективне число витків котушки. Для розглянутого на мал. 4 случаючи} w_э= /Ф₄=48/8=6

_{Можна також зробити заміну реальної котушки на еквівалентну зі збереженням числа витків}  = wФ_n. _{. Тоді для збереження потокозчеплення необхідно прийняти, що з усіма витками котушки зчіплюється магнітний потік} Ф_n=  /w .

_.

_{Перший варіант заміни котушки еквівалентної зберігає картину магнітного полючи, змінюючи параметри котушки, другий - зберігає параметри котушки, змінюючи картину магнітного полючи.}

_{Зв´язок вихрового електричного полю з магнітним.}

_{Так, у багатьох роботах виникнення вихрового електричного полючи розглядається як результат лінійного руху електронів по провіднику.}

_{Більш об'єктивне спостереження даного явища, при якому джерело струму розглядається в нерозривному зв'язку з виникаючим вихровим магнітним полем, дозволяє зробити наступний висновок: вихрове магнітне поле створюється (є антиподом) вихрового електричного полючи.}

_{Порівняння результатів спостереження Суб'єктивним і Об'єктивним спостерігачем того самого експерименту приведене на мал. 1.}

_{Рис.1. Суб'єктивне й Об'єктивне спостереження причин виникнення вихрового магнітного полючи.}

_{Графічно схема даного спостереження в двомірному континуумі об'єктивно описана ТСП, як спостереження другого рівня ИЯ.}

Л.С.Жданов. Підручник по фізиці для середніх спеціальних навчальних закладів. § 26.1 25.12.-25.13 стор.275 – 276, 291

Питання для самоперевірки.

1. _{Чим відрізняється магнітний потік та потокозчеплення?}

2. _{Від яких величин залежить магнітна індукція?.}

3. _{В чому полягає зв´язок електричного полю з магнітним?}

_{3.8 Тема 4.}

Вихрові струми , електрорушійна сила. Діюче значення е.р.с., напруга. Електричний резонанс..

План.

1. Вихрові струми , електрорушійна сила.

2. Явище електромагнітної індукції

3. Сутність основного закону електромагнітної індукції.

4. Явище самоіндукції.

5. Електричний резонанс.

Вихрові струми , електрорушійна сила.

Вихрові струми, струми Фуко (на честь Фуко Жан Бернар Леон) — вихрові індукційні струми, які виникають у масивних провідниках при зміні магнітного потоку, який їх пронизує.

Вперше вихрові струми виявлені французьким ученим Д.Ф Араго (1786—1853) в 1824 р. у мідному диску, розташованому на осі під магнітною стрілкою, яка оберталася. За рахунок вихрових струмів диск теж обертався. Це явище, назване явищем Араго, було пояснене декілька років по тому M. Фарадеєм з позицій відкритого ним закону електромагнітної індукції: магнітне поле, яке обертається, індукує у мідному диску струми (вихрові), які взаємодіють з магнітною стрілкою. Вихрові струми названі на честь французького фізика Фуко (1819—1868). Він відкрив явище нагрівання металевих тіл, які обертаються у магнітному полі, вихровими струмами.

Струми Фуко виникають під дією змінного електромагнітного поля і за своєю фізичною природою нічим не відрізняються від індукційних струмів, що виникають у лінійних проводах.

Так як електричний опір проводників малий, то сила струмів Фуко може досягати великих значень. Згідно з правилом Ленца вони вибирають у провіднику такий напрямок, щоб протистояти причині, яка їх викликає. Тому у сильному магнітному полі провідники, які рухаються, витримують сильне гальмування, яке пояснюється взаємодією струмів Фуко з магнітни полем. Цей ефект застосовується для демпфування рухливих частин гальванометрів, сейсмографів тощо.

Теплова дія струмів Фуко використовується в індукційних печах — у котушку, яка живиться від високочастотної батареї великої сили поміщають тіло-провідник у якому виникають вихрові струми, які розігрівають його до плавлення.

У багатьох випадках струми Фуко небажані, шкідливі. Для боротьби з ними приймаються спеціальні заходи: наприклад, якоря трансформаторів набираються з тонких пластин. Поява феритів зробила можливим виготовлення цих провідників суцільними.

_{ЯВИЩЕ ЕЛЕКТРОМАГНІТНОЇ ІНДУКЦІЇ}

_{Це явище полягає в тому, що при зміні магнітного потоку, охоплюваного контуром провідника, в останньому виникає ЕРС індукції, що створюється в провіднику індукційний струм.}

_{Величина е.р. с. індукції. При виконанні досвідів Фарадея можна бачити, що стрілка гальванометра відхиляється тим далі, ніж швидше скується в соленоїд чи магніт котушка зі струмом. Те ж саме вийде, якщо підсилити магнітне поле первинної котушки, збільшивши в ній струм.}

_{Більш докладне вивчення цього явища показало, що е.р с. індукції, що виникає в якому-небудь ланцюзі, прямо пропорційна і швидкості зміни потокозчеплення магнітного полю з цим ланцюгом:}

Еинд=-Δψ/Δt

_{Відзначимо, що коли ланцюг складається з одного витка, тобто є простим контуром, то формула (26.6) приймає вид}

Еинд=-ΔФ/Δt

_{У цих формулах Δt - час, за яке відбувається зміна потокозчеплення на ΔФ . Якщо Δt дуже мало, те формули(26.6) дають миттєве значення е.р. с. індукції. Якщо ж Δt велико, то при підрахунку по цих формулах виходить середнє значення е.р. с. індукції.}

_{Знак мінус у формулах показує, що, коли потокозчеплення зменшується (ΔФ негативно), е.р. с. створює індукційний струм, що збільшує потокозчеплення, і навпаки. Таким чином, знак мінус показує, що відповідно до закону Ленца е.р. с. індукції повинна перешкоджати причині, що викликає її поява. З формули (26.ба) видно, що одиницю виміру магнітного потоку в системі СІ можна називати вольт-секундою, тому що} ΔФ׀=׀ЕиндΔt׀, 1Вб=1В с

_{ОСНОВНИЙ ЗАКОН ЕЛЕКТРОМАГНІТНОЇ ІНДУКЦІЇ ФАРАДЕЯ-ЛЕНЦА.}

_{Середнє значення ЭДС індукції (Е), що створює індукційний струм, пропорційно швидкості зміни магнітного потоку:}

_{Е =-ΔФ./Δt, де}

_{Δф. = Ф1. –Ф2. -зміна магнітного потоку,}

_{Δt= t2 –t1 - час, за яке ця зміна відбулася.}

_{ЭДС індукції в даний момент часу в загальному випадку можна визначить як похідну потоку за часом:}

_{Е = - Ф. .}

_{Знак мінус відбиває правило Ленца, що визначає напрямок індукційного струму. Індукційний струм завжди спрямований так, що його магнітне поле протидіє тій зміні магнітного потоку, що викликає цей струм.}

_{ЯВИЩЕ САМОІНДУКЦІЇ}

_{Явище самоіндукції полягає в тому, що ЭДС індукції виникає в провіднику зі струмом при зміні власного магнітного потоку, створюваного цим струмом. Явище самоіндукції виникає завжди, коли по провіднику йде струм, що змінюються по чи величині по величині і напрямку.}

_{ЭДС самоіндукції визначають також за законом Фарадея:}

_{Е=LΔІ/Δt, де}

_{ΔІ=І2 –І1 - зміна сили струму,}

_{Δt=t2 –t1 - час, за яке ця зміна відбулася,}

_{L- Індуктивність провідника.}

_{Електричний резонанс..}

_{ВСТУПНА ЧАСТИНА}

_{Резонанс - це такий стан резистивно-индуктивно-емкостной схеми, коли індуктивний опір і ємнісний опір однакові. Оскільки ці реактивні опори однакові, вони цілком компенсують один одного. o При резонансі мають місце багато спеціальних ефектів. Наприклад, у силу того, що реактивні}

_{опори цілком гасять один одного, схема виявляє себе як цілком резистивная.}

_{Ви зможете знайти резонансні схеми майже у всіх типах електронного устаткування. Вони широко використовуються для виконання різних задач настроювання і фільтрації в електронному устаткуванні. У даному експерименті Ви розглянете ефект резонансу як у рівнобіжних, так і в послідовних схемах.}

_{Послідовний резонансний контур}

_{Послідовний резонансний контур представлений на малюнку 22-1. Згадаєте, що при наявності резонансу в схемі індуктивний опір і ємнісний опір цілком компенсують один одного, і опір току робить один лише активний опір схеми. У такій схемі повний опір попросту дорівнює значенню R плюс опір постійному струму котушки. Головною характеристикою послідовного резонансного контуру є те, що його повний опір мінімальний при резонансі. При настроюванні частоти на величину, що перевищує чи лежать нижче резонансної частоти, повне опір зростає.}

_{Оскільки при резонансі в послідовному резонансному контурі повний опір мінімально, струм у контурі зростає до пікової величини. Ця велика величина струму при її множенні на індуктивний опір і на ємнісний опір дає дуже високі спадання напруги на котушці індуктивності і на конденсаторі. У дійсності спадання напруги на котушці індуктивності і на конденсаторі}

_{в умовах резонансу часто значно перевищують напруга харчування. Ці надзвичайно високі при резонансі напруги називаються стрибками напруги при чи резонансі резонансними підвищеннями напруги.}

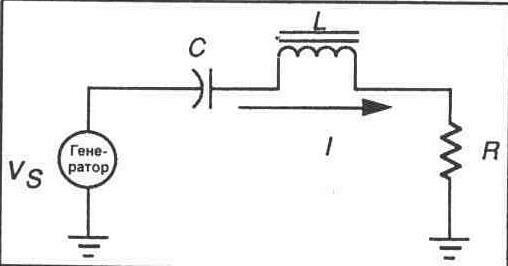
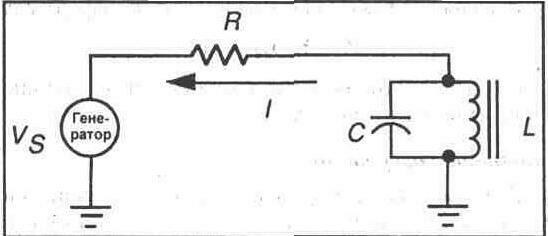
_{Мал. 22-1. Рівнобіжний резонансний контур}

_{Рівнобіжний резонансний контур представлений на малюнку 22-2. Конденсатор і котушка індуктивності з'єднуються паралельно один з одним, і вся комбінація іноді з'єднується послідовно з резистором. Оскільки при резонансі індуктивний опір і ємнісний опір цілком компенсують один одного, схема виявляє дуже значний активний опір. У такій схемі повний опір рівнобіжного індуктивно-ємнісного контуру зростає до багатьох тисяч Ом при резонансі. При частотах, що перевищують чи лежить нижче резонансної частоти, повне опір зменшується.}

_{мал... 22-2.}

_{Якщо Ви вимірите лінійний струм у резисторі, з'єднаному послідовно з рівнобіжним резонансним контуром, Ви знайдете, що струм досягає мінімуму в умовах резонансу. Це відбувається внаслідок того, що при резонансі повний опір максимальний,і,отже, це приводить до формування мінімальної величини струму через контур. При зміні частоти в будь-яку сторону від резонансної частоти повний опір контуру зменшується, і лінійний струм зростає.}

_{Повний опір рівнобіжного резонансного контуру обчислюється на підставі наступної формули:}

Z=L/CR

_{У цій формулі: R - опір котушки індуктивності L. Наприклад, якщо L = 2 мГн, З = 0,05 мкФ і R = 5 Ом, повне опорів Z дорівнює:}

Z = 2 х 10^-3 / (0,05 х 10 ^-6)(5)

Z = 8000 Ом

_{Ви можете також використовувати таку формулу:}

Z = Rw(Q² + 1)

_{де: Rw- це опір обмотки котушки індуктивності і Q = Xl/Rw.}

_{Короткий зміст}

_{Як було зазначено раніше, у даному експерименті Ви зберете послідовний резонансний контур і рівнобіжний резонансний контур, а також познайомитеся з деякими зі згаданих ефектів. Ви практично розрахуєте резонансну частоту (fг ) при заданих значеннях індуктивності і ємності. Це здійснюється за допомогою наступної формули}

fr = 1 / 2*3.14(LC)^0.5

_{Амплітуда змушених коливань тим більше, ніж ближче час тота е.р. с. до частоти вільних коливань у контурі. При збігу цих частот амплітуда стає найбільшої, виходить електричний резонанс: струм у контурі і напруга на його конденсаторі можуть дуже сильно перевищувати ті, котрі виходять при відбудуванні, т.. е. удалині від резонансу. Резонансні явища виражені тим сильніше і різкіше, чим менше опір контуру, що, таким чином, і тут грає таку ж роль, як тертя в механічній системі.}

_{Усі ці явища легко спостерігати, використовуючи для одержання гармонійної е.р. с. міський перемінний струм і побудувавши коливальний контур, власну частоту якого можна змінювати в обидва боки від частоти струму (50 Гц). Щоб уникнути при цьому високих резонансних напруг у контурі, що (при напрузі в міській мережі 220 В) можуть досягти декількох кіловольтів, варто скористатися понижуючим трансформатором.}

_{На мал. 53 показане розташування приладів і електрична схема досвіду (позначення на малюнку і на схемі однакові). У схему включений понижуючий трансформатор 1, конденсатор 2, дроселі 3 і 4, що представляють собою котушки індуктивності з залізними сердечниками, що потрібні для одержання необхідної великої індуктивності. Для зручності настроювання контуру індуктивність його складена з індуктивностей двох окремих котушок. Настроювання здійснюється тим, що в одного з дроселів (4) сердечник має повітряний зазор, ширину якого можна плавно змінювати в межах 2-4 мм, змінюючи тим самим загальну індуктивність. Ніж ширше зазор, тим менше індуктивність. У підписі до мал. 53 зазначені зразкові значення усіх величин. Напруга на конденсаторі виміряється вольтметром перемінного струму В, а амперметр перемінного струму А дозволяє стежити за струмом у контурі.}

_{Досвід показує наступне: при малій індуктивності контуру напруга на конденсаторі складає деяким більш, ніж наводиться в контурі е.р. с. з, тобто трохи вольт. Збільшуючи індуктивність, ми побачимо, що напруга росте; це наростання стає усе більш і більш різким у міру наближення до резонансного значення індуктивності. При тих числових даних, що зазначені в підписі до мал. 53, напруга піднімається вище 60 В. При подальшому збільшенні індуктивності напруга знову падає. Тік у контурі змінюється пропорційно напрузі на конденсаторі і при резонансі може дійти до 20 мА.}

_{Цей досвід відповідає механічному досвіду з вантажем на пружині, що був описаний у § 12. Там нам було зручно змінювати частоту діючої сили, тут же ми проходимо через резонансне настроювання, змінюючи власну частоту коливальної системи - нашого контуру. Сутність явища резонансу від цього не міняється.}

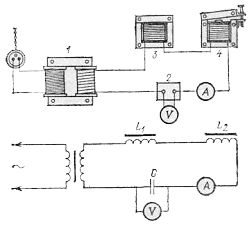
Мал. 53. Одержання електричного резонансу на частоту міського струму: 1 - трансформатор, що знижує напруга, наприклад з 220 до 6 В, 2 - конденсатор ємності З=1,2 мкФ, 3 - дросель, індуктивність якого L1=7,5 Гн, а опір обмотки дорівнює 80 Ом, 4 - дросель з перемінним повітряним зазором, індуктивність якого L2=8,3 Гн при ширині зазору 2-3 мм і змінюється при зміні ширини зазору на 15-20% в обидва боки від зазначеного (резонансного) значення

Роль електричного резонансу в техніку величезна. Приведемо лише один приклад.

Власне кажучи на резонансі заснована техніка радіоприймача . Численні радіостанції випромінюють електромагнітні хвилі, що наводять в антені радіоприймача перемінні е.р. с. (електричні коливання), причому кожна радіостанція наводить коливання своєї визначеної частоти. Якби ми не уміли виділити з цієї складної суміші коливань коливання, що наводяться цікавлячи нас радіостанцією, то ніякий радіоприйом не був би можливий. Тут і приходить на допомогу електричний резонанс.

Ми з'єднуємо з антеною коливальний контур, наприклад через індуктивність, як показано на мал. 54.

Ємність конденсатора можна плавно змінювати, змінюючи тим самим власну частоту контуру. Якщо ми настроїмо контур на бажану частоту, наприклад n1, то е.р.с. з частотою n1 викликає в контурі сильні змушені коливання, а всі інші е.р. с. слабкі. Слідів _отже:

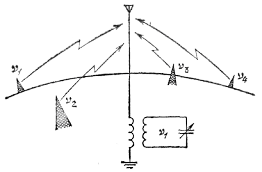
_{Мал. 54. Резонанс дозволяє набудовуватися на бажану станцію і відбудовуватися від всіх інших.}

_{Стрілка на конденсаторі вказує на те, що ємність конденсатора можна змінювати}

_{резонанс дозволяє за бажанням набудовувати приймач на частоту обраної станції.}

_{Зрозуміло, в електротехніку, як і в машинобудуванні, резонанс може з'явитися найбільшим злом там, де його не повинне бути. Якщо електричний ланцюг розрахований на роботу під час відсутності резонансу, то виникнення резонансу викликає аварію: проводи розжаряться від надмірно сильних струмів, ізоляція буде пробита через високі резонансні напруги, і т.п.. У минулому столітті, коли електричні коливання були ще недостатньо вивчені, такі аварії случалися. Тепер же ми вміємо в залежності від умов або використовувати резонанс, або усувати його.}

Л.С.Жданов. Підручник по фізиці для середніх спеціальних навчальних закладів. § 26.6 26.9.-26.10 стор. 298 - 303.

Питання для самоперевірки.

1. _{Як визначити електрорушійну силу?}

2. _{В чому полягає явище електромагнітної індукції?}

3. _{В чому полягає сутність основного закону електромагнітної індукції?}

4. _{Чим відрізняється самоіндукція?}

5. _{Сутність резонансу?}

6. _{Яки бувають види резонансного контуру?}

3.9 .РІШЕННЯ ЗАДАЧ ПО ЕЛЕКТРОМАГНЕТИЗМУ

1) При рішення задач про сили, що діють на провідник зі струмом у магнітному полі, варто зробити схематичне креслення, на якому зобразите провідник зі струмом, силові лінії магнітного полючи, кут між напрямком токаї полючи. Використовуючи правило лівої руки, визначите напрямок сили Ампера. Якщо в задачі розглядається рівновага провідника зі струмом у магнітному полі, то , крім сили Ампера, потрібно вказати і всі сили, що діють на провідник. Умова рівноваги провідника виражається рівняннями механіки.

2) Рішення задач про рух заряджених часток в електричному і магнітному полях варто також почати з побудови схематичного креслення, на якому потрібно вказати силові лінії електричних і магнітних полів, проставити вектор початкової швидкості частки і відзначити знак її заряду, тому що від знака заряду залежить напрямок сили Лоренца.

Якщо вектор швидкості частки спрямований під кутом до лінії індукції магнітного полючи, розкладете його на дві складові, одна з яких повинна бути спрямована перпендикулярно вектору магнітної індукції, а друга паралельно йому. Це спрощує рішення, тому що уздовж магнітного полючи сила Лоренца не діє.

Укажіть усі сили, що діють на частку. Дія сили ваги на елементарні частки не потрібно враховувати, тому що вона мізерно мала в порівнянні із силами електромагнітного полючи.

Рівняння для рішення задачі складаються відповідно до законів динаміки матеріальної крапки.

3) Якщо в задачі розглядається явище електромагнітної індукції, ЭДС, що виникає в провіднику. Можна визначити за законом електромагнітної індукції. При цьому насамперед , установите причину зміни магнітного потоку: чи змінюється магнітне поле, у якому знаходиться провідник; чи площа, крізь яку розглядається потік; чи орієнтація провідника в магнітному полі.

Якщо провідник замкнуть, у ньому будуть виникати електричний струм. Додаткові рівняння для рішення задачі можна скласти, використовуючи співвідношення і закони постійного струму.

_{3.9.1.Приклади рішення задач}

ЗАДАЧА 1.

Визначити енергію магнітного поля соленоїда , в якому при силі струму 10А виникає магнітний потік 0.5 Вб.

Дано: Рішення

І = 10А енергія магнітного поля, створюваного соленоїдом

Ф = 0.5 Вб залежить від індуктивності та квадрата

W = ? сили струму: W = LI²\2.

Магнітний потік, створюваний струмом соленоїда, залежить від індуктивності провідника : Ф = LI

Виконаємо постановку, отримаємо:

W = ФI\2

Виконаємо обчислення:

W= 0.5 Вб 10 А\2 = 2.5 Дж.

ЗАДАЧА 2.

Плоска дротова рамка, що складається з одного витка, що має опір

1·10 ^-3 Ом і площа 1 см², пронизіваеться одноріднім магнітнім полем. напрямок ліній магнітної індукції перпендикулярно площини рамки. Індукція магнітного полючи змінюється на 0.01 Вб\ м² за 1 с. Яка кількість теплоті віделяеться у витку за одиницю часу?

Дано :

Рішення.

S = 1 см² 1·10^-4м²

∆В = 0.01 Вб\м²

t = 1с

N = ?

Кількість теплоті, що віддається витком зі струмом навколишньої маренні в одиницю години, визначається тепловий потужністю:

N = U²\R

Напруга в витке дорівнює ЕРС індукції, створюваної змінним магнітним полем, т.б. U = Е_1.

По закону Фарадея: Е₁ = - ∆Ф\∆t.

По визначенню Ф = вScosφ

напрямку ліній магнітної індукції, тому cosφ = 1.

Магнітний потік в даному випадку змінюються за рахунок зміни магнітного поля, тому

∆Ф = Ф₂ - Ф₁ = S∆В

Зробив підстановку N = (∆В)²S²/t²R

Виконаємо обчислення:

N = 1·10^-4 ·1·10^-6\ 1·10^-3 =10^-9(Дж\с).

3.9.2.ЗАДАЧІ ДЛЯ САМОСТІЙНОГО РІШЕННЯ

1.Визначите магнітний потік, що проходить крізь сонячну пляму площею 1,2*10¹⁵ м² , якщо середня індукція магнітного полючи дорівнює 0.3 Тл. Лінії індукції магнітного полючи плями перпендикулярні го поверхні.

Відповідь:3.6*10¹⁴ Вб.

2.В однорідному магнітному полі з індукцією 15 Тл провідник перемістився перпендикулярно лініям магнітної індукції на 10 см. Яку роботу зробив при цьому електричний струм, якщо довжина активної частини провідника 40 см, а сила струму в ньому 2 А?

Відповідь:1.2 Дж.

3.Визначите енергію магнітного полючи котушки, у якій при силі струму 8А виникає магнітний потік 0.6 Вб.

Відповідь:2.4 Дж

4. По горизонтально розташованому провіднику довжиною 20 см і масою 4 м тече струм 10А. Знайдіть модуль магнітного полючи, у яке потрібно помістити провідник, щоб сила ваги зрівноважилася силою Ампера.

Відповідь:0.02 Тл.

5.Між полюсами магніту на двох тонких нитках підвішений горизонтально тонкий провідник масою 10 м і довжиною 0.2 м. Індукція однорідного магнітного полючи 0.25 Тл і спрямована вертикально. Весь провідник знаходиться в магнітному полі. На який кут від вертикалі відхиляться нитки, що підтримують провідник, якщо по ньому пропустити струм 2 А? Вагою ниток зневажити.

Відповідь: 45º .

6.На скількох амперів у секунду повинний мінятися струм, щоб в обмотці електромагніта з індуктивністю 3.5 Гн збуджувалася ЕРС самоіндукції 70 В?

Відповідь: 20 А /с.

7. Який магнітний потік пронизував кожен виток котушки, що має 1000 витків, якщо при рівномірному зникненні магнітного полючи протягом 0.1 с. у котушці індуцируються ЕРС 10 В.

Відповідь: 0.001 Вб.

8.Швидкість літака дорівнює 900 км/ч. Знайдіть різницю потенціалів, що виникає між кінцями крил літака, якщо вертикальна складова земного магнітного полючи 5*10^-5 Тл. і розмах крил літака 12 м. Літак летить горизонтально.

Відповідь: 0.15 В.

9.З якою швидкістю треба переміщати провідник, довжина активної частини якого 0.5 м, під кутом 50º до вектора магнітної індукції, модуль якого дорівнює 0.8 Тл, щоб у провіднику збудилося ЕРС індукції 2. А?

Відповідь: 6.53 м/с .

10.Замкнута котушка діаметром 8 мм, що містить 1000 витків, поміщена в однорідне магнітне поле 10 мТл. Площина котушки перпендикулярна до ліній магнітної індукції. Який заряд протече по котушці, якщо неї повернути на 180º ? Опір котушки 10 кОм

Відповідь: 1*10^-7 Кл.

11.До джерела струму з ЕРС 40 В и внутрішнім опором 1 Ом приєднали котушку з опором 3 Ом. Визначите індуктивність котушки, якщо при встановленні постійного струму енергія магнітного полючи в котушці дорівнює 7.5 Дж. Яке середнє значення ЭДС самоіндукції в контурі при розмиканні ланцюга за 1.2*10^-2 с.

Відповідь: 0.15 Гн; 125 В.

Розділ 4. Коливання і хвилі.