2. Расчетно-графическая работа №1

Исследование линейных электрических цепей постоянного тока Раздел "Линейные электрические цепи постоянного тока" в курсе "Теоретические основы электротехники" ставит следующие задачи:

a) изучение законов Ома и Кирхгофа и методов расчета цепей постоянного тока, основанных на этих законах:

б) применение этих методов для расчета цепей.

Поэтому основной целью первой контрольной работы является закрепление теоретических знаний, полученных после проработки литературы [3-6] путем выполнения расчетов сложной цепи с несколькими источниками питания.

Задача 1.

Для электрической схемы, соответствующей номеру варианта и изображенной на рисунке, даны сопротивления резисторов и некоторые показания приборов. Определить токи во всех ветвях и показания остальных приборов.

Схема и ее параметры определяются из таблицы 1, согласно варианту.

Таблица 1

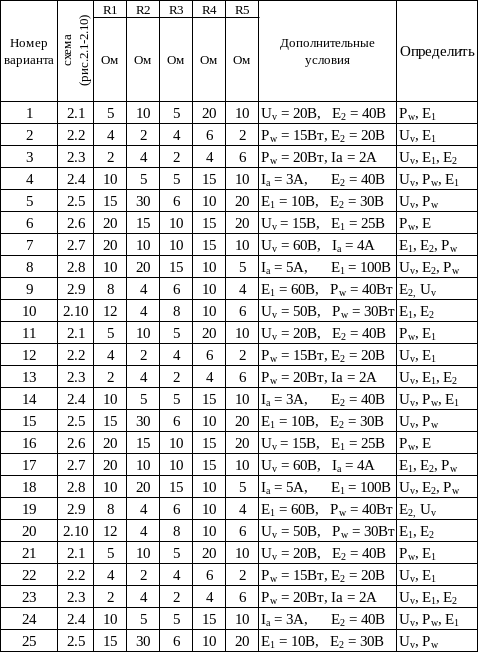
Таблица 1 (продолжение)

2.2 Методические указания к выполнению ргр № 1

Задача 1

1. Проработать материал, изложенный в литературе [3-6]

2. Следует выписать и усвоить основные законы цепей постоянного тока: Ома, Кирхгофа, Джоуля-Ленца. При этом важно уяснить разницу закона Ома для пассивного (рис.2.21, а) и активного (рис. 2.21, б) участков цепи.

При использовании закона Ома нужно иметь в виду, что если направление величины или не совпадает с выбранным направлением тока, то в формулах закона Ома знак этих величин изменяется на отрицательный.

3. Законы Кирхгофа — основные законы электротехники. Первый закон Кирхгофа применяется к узлам электрической цепи: алгебраическая сумма токов в узле равна нулю, т.е., , где — число ветвей, соединенных в данном узле. Токи одного направления, например, притекающие к узлу, записываются со знаком плюс, токи противоположного направления, например, оттекающие от узла ,— со знаком минус.

Второй закон Кирхгофа применяется к контурам электрической цепи: алгебраическая сумма ЭДС в контуре электрической цепи равна алгебраической сумме напряжений в этом контуре, т.е. , где — число ЭДС в контуре; — число напряжений в контуре. ЭДС и напряжения берут со знаком плюс, если их направление совпадает с принятым направлением обхода контура.

4. Закон Джоуля-Ленца: для пассивных участков цепи постоянного тока , где - потребляемая энергия: - напряжение на пассивном участке: -ток; - время. Мощность . Мощность, вырабатываемая источником ЭДС, . Если ЭДС и ток имеют разные знаки, то мощность источника отрицательна. Это означает, что данный источник не генерирует, а потребляет энергию.

5. При решении задач часто применяют метод преобразования цепи с целью ее упрощения. При последовательном соединении резисторов эквивалентное сопротивление , где — число последовательно соединенных резисторов.

При параллельном соединении резисторов эквивалентная проводимость , где - число параллельно соединенных резисторов.

При смешанном соединении резисторов эквивалентное сопротивление находят путем постепенного упрощения преобразуемого участка схемы и приведения его к одному сопротивлению. При расчете токов в отдельных ветвях схему "разворачивают" в обратном порядке.

Часто схему можно значительно упростить, если использовать преобразование "треугольника" сопротивлений в трехлучевую "звезду" сопротивлений или наоборот.

При взаимном преобразовании пассивной трехлучевой "звезды" (рис.2.22,а) и "треугольника" (рис.2.22,б) сопротивлений имеем:

рис 2.22

Пример

Для цепи (рис.2.23.) найти токи во всех ветвях и ЭДС источников и , если известны сопротивления резисторов и показания амперметров и .

Решение

Упростим схему, преобразовав "звезду" сопротивлений в эквивалентный "треугольник" сопротивлений (рис. 2.24.).

Резисторы и соединены параллельно. Их сопротивление

Резисторы , и также соединены параллельно.

. Величину ЭДС можно определить по закону Ома

После эквивалентных преобразований получаем схему, представленную на рис.2.25.

Заменим "треугольник" сопротивлений на "звезду" , (рис. 2.26.)

По второму закону Кирхгофа для первого контура имеем

. (1)

Ток можно выразить по первому закону Кирхгофа через ток :

. (2)

Решив совместно уравнения (1) и (2), определим ток :

ЭДС можно определить по второму закону Кирхгофа, составив уравнение для второго контура

Теперь рассмотрим исходную схему (см. рис.2.23) и определим токи в ветвях, используя законы Кирхгофа.

Сделать выводы по работе