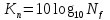0.25 Балл.

Задание №8

Определите коэффициент шума усилительного прибора в дБ, если его эффективная шумовая температура (100+ Nstudent*2)К.

Рассчитайте эффективную шумовую температуру двух таких приборов, включенных каскадно, если коэффициент усиления каждого прибора 13 дБ.

Дано:

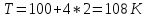
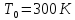
Решение:

1. 

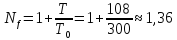- фактор шума

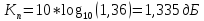
2. Расчет эффективной шумовой температуры двух приборов, включенных каскадно.

Фактор шума каскадно включённых усилителей определяется по формуле Фрииса:

;

=

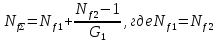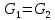
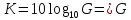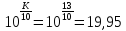
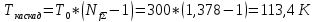
Ответы:

1)

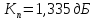
2)

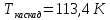
1 Балл.

Задание №9

Объясните, где «работает» формула Найквиста, а где Ван-дер-Зила при расчете шумов.

В чем разница введения понятий «эффективная» шумовая температура и «эффективное» шумовое сопротивление?

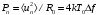- формулa Найквиста для теплового шума в случае термодинамического равновесия. Однако в реальных приборах условия такого равновесия нарушаются из-за наличия встроенных или приложенных «греющих» электрических полей, которые изменяют энергию электрических зарядов, а значит и величину шумовых флюктуаций. В таких случаях считают эквивалентные шумовые параметры, используя формулу А. Ван дер Зила:

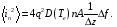, где

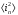- средний квадрат шумового тока

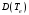диффузия заряженных частиц общим числом ,

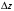- резистор с температурой носителей

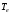- температура носителей в полосе частот

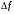- полоса частот.

- поперечное сечение рассматриваемого элемента.

Формула А. Ван дер Зила используется для более точных расчетов в реальных приборах и при термодинамическом равновесии трансформируется в формулу Найквиста

Действительно, в случае термодинамического равновесия между коэффициентом диффузии и подвижностью носителей 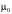существует взаимосвязь, выраженная соотношением Эйнштейна - 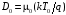. После некоторых преобразований, вводя понятие эффективной шумовой температуры 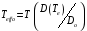или эффективной шумовой проводимости 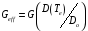, получим обычную запись формулы Найквиста для отсутствия термодинамического равновесия:

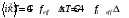
Шумовая температура - температура, вызванная излучением окружающей антенну среды в отсутствие источника и тепловыми потерями в облучающей системе. Она задается формулой Найквиста, и равна температуре резистора, который имел бы такую же мощность тепловых шумов в данной полосе частот

Шумовое сопротивление может быть интерпретировано как параметр, определяющий флуктуационное напряжение на входе, возникающее за счет тепловых шумов.

0.5 Балл.

Задание №10

Прокомментируйте формулу для мощности взаимодействия электромагнитного поля и потока заряженных частиц. В чем заключается сложность нахождения данного интеграла?

Свяжите решение с задачей №7.

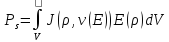
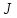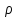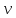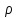Данная формула позволяет вычислить мощность взаимодействия электромагнитного поля и потока заряженных частиц в пространстве их взаимодействия. Плотность потока заряженных частиц зависит от объёмной плотности заряда и скорости частиц, а скорость, в свою очередь, - функция поля E, что также зависит от . Таким образом, сами летящие заряды создают поле, и это поле действует на эти же заряды.

Сложность вычисления интеграла заключается в трудности учесть все факторы. Например, для нахождения плотности потока нужно знать скорость частиц, которая находится из уравнений движения (например, законов Ньютона или кинетического уравнения Больцмана) и напряженность поля, которая находится из уравнений Максвелла, а также принять во внимание граничные условия, которые определяются параметрами пространства взаимодействия.

В задаче 7 рассматривался энергообмен в зазоре конечной ширины, где в отличие от бесконечно узкого зазора, изменяется и скорость, и взаимное положение электронов. Ускоренные электроны пролетают через зазор за меньшее время, чем замедленные, поэтому коэффициент взаимодействия M для ускоренных электронов оказывается больше, чем для замедленных. В результате ускоренные электроны приобретают большие скорости, чем замедленные, т.е. в целом электронный поток на выходе резонатора имеет большую кинетическую энергию, чем на входе. Избыток кинетической энергии электроны получают от электромагнитного поля зазора, что и отражено на эквивалентной схеме резонатора в виде включённой параллельно зазору электронной проводимости.

Средняя мощность взаимодействия поля зазора с электронным потоком может быть найдена по формуле: