Программирование на BASIC / Visual Basic / Курсовая работа по Visual Basic

Министерство образования и науки Российской Федерации

Уфимский Государственный Авиационный Технический Университет

Кафедра информатики

Пояснительная записка

к курсовой работе

«Решение систем линейных уравнений. Метод Гаусса»

Тема 2, Вариант 4

Выполнил:

студент

Проверил:

Белорецк 2008

Содержание:

1. Введение 3

2. Постановка задачи 4

3. Теоретическая часть 5

4. Блок-схема метода решения СЛАУ методом Гаусса 7

5. Описание программы. Исходный тест программы. 9

8. Список использованной литературы. 15

1. Введение

В данной курсовой работе рассмотрен один из методов вычислений системы линейных алгебраических уравнений – метод Гаусса. Для решения системы составлена программа – приложение win32 в среде Microsoft Visual Basic 6.0 for 32-bit Windows Development. В пояснительной записке рассмотрена теория метода Гаусса, представлена блок-схема метода, описана структура программы и основных компонентов. Дан код ядра программы и описана графическая часть программы – визуализации с использованием компонента PictureBox.

2. Постановка задачи

Таблица 1.

№п/п № вар.	1 Методы	2	3	4
				Визуализация
1	1	1	1	При N=2
2	2	1	1
3	3	1	1
4	1	2	2
5	2	2	2
6	3	2	2
7	1	2	3
8	2	1	3
9	3	2	3

Таблица 2.

1	2	3
Методы решения	Исходные данные	Вывод результатов
1. метод Гаусса 2. метод Халецкого 3. метод Крамера	Порядок системы N<=10. Коэффициенты задаются следующими способами: 1. из текстового файла 2. с клавиатуры Перед решением системы проверить исходные данные на корректность	1 - FlexGrid 2 –PictureBox 3 - файл

Решить систему линейных алгебраических уравнений методом Гаусса. Порядок системы N<=10.

Коэффициенты задаются с клавиатуры. Перед решением системы проверить исходные данные на корректность. Результат вывести в PictureBox. Визуализация – при n = 2.

3. Теоретическая часть

Метод Гаусса

С помощью этого метода решают неоднородную систему n линейных алгебраических уравнений с n неизвестными:

a₁₁x₁ + a₁₂x₂ + ... +a_1n x_n = a_1n+1

a₂₁ x₁ + a₂₂ x₂ + ... +a_2n x_n = a_2n+1

....

a_n1 x₁ + a_n2 x₂ + ... +a_nn x_n = a_nn+1

Вначале находим отличный от нуля коэффициент при x₁ . Соответствующее уравнение переставляем с первым (если это необходимо!!!). Получаем систему с a₁₁ отличным от нуля. Разделив коэффициенты этого уравнения на a₁₁ , получим:

x₁ + b₁₂ x₂ + ... + b_1n x_n = b_1n+1

При помощи этого уравнения исключаем x₁ из исходной системы:

a ₍₁₎₂₂ x₂ + a ₍₁₎₂₃ x₃ + ... + a _(1)2n x_n = a _(1)2n+1

....

a _{(1)n2 x2} + a _(1)n3 x₃ + ... + a _(1)nn x_n = a _(1)nn+1

где

a _(1)ij = a_ij - a_i1 b_1j , i,j= 2...n

и Т.Д.

Полученная система содержит n-1 уравнение. Применяем описанную выше процедуру к этой системе. Операции повторяем требуемое число раз, пока не приведем систему к треугольному виду:

x₁ + с₁₂ x₂ + ... + с_1n x_n = с_1n+1

x₂ + ... + c_2n x_n = c_2n+1

....

x_n = c_nn+1

Теперь легко определить x_n , x_n-1 , ..., x₁ .

Если при поиске отличного от нуля коэффициента такого не окажется, то матрица системы вырождена и алгоритм неприменим. Для сравнения с нолем в алгоритм передается малое число epsilon, и любое число, по модулю меньшее epsilon, считается нолем. В случае вырожденной матрицы функция возвращает False. Если матрица невырождена, то функция возвращает True, а переменная X содержит решение системы.

4. Блок-схема метода решения СЛАУ методом Гаусса

Рис.1. Блок-схема решения СЛАУ методом Гаусса (продолжение на след.стр.).

Рис.2. Блок-схема решения СЛАУ методом Гаусса (продолжение).

5. Описание программы. Исходный тест программы.

Эта программа создана, как многооконное приложение. Данные о нашем линейном уравнении мы вводим с клавиатуры. Далее с помощью падающего меню «Система линейных уравнений», нажатием кнопки «Вычислить», ответ выводиться в файл и в PictureBox1, а в PictureBox2 выводиться графическое решение. Там же можем посмотреть блок-схему самого метода Гаусса. В меню «Справка» выводится информация об авторе

Программа состоит из нескольких форм. Формы их назначение описаны в таблице 3.

Таблица 3. Формы программы.

Форма	Назначение
Form1	Главное окно программы. На данной форме расположено главное меню программы: Файл Решение СЛАУ методом Гаусса О программе. А так же расположена кнопка «Блок-схема метода», вызывающую form4, содержащую рисунок блок-схемы метода Гаусса.
Form2	Форма ввода значений, вычисления корней СЛАУ и визуализации при n = 2.
Form3	Форма «О программе»
Form4	Форма с алгоритмом метода Гаусса. Вызывается кнопкой «Блок-схема метода».

Рис. 3. Общий вид программы.

Визуализация вычислений при n=2 сделана автоматически - в зависимости от вводимого n. При n> 2 графики не выводятся.

Исходный текст программы:

Private Sub Command1_Click()

Picture1.Cls

Picture2.Cls

n = Val(Text1)

Dim A() As Double

Dim B() As Double

Dim x() As Double

ReDim A(1 To n, 1 To n + 1)

ReDim B(1 To n + 1)

ReDim x(1 To n)

p = Split(Text2, "/")

k = 0

For i = 1 To n

For j = 1 To n + 1

A(i, j) = p(k)

k = k + 1

Next j

Next i

If n = 2 Then

Picture2.Scale (-10, 25)-(12, -5)

For i = -10 To 12

Picture2.Line (i, -5)-(i, 25), RGB(200, 220, 225)

Picture2.PSet (i, 0)

Picture2.Print i

Next

For i = -5 To 25

Picture2.Line (-10, i)-(12, i), RGB(200, 220, 225)

Picture2.PSet (0, i)

Picture2.Print i

Next

Picture2.Line (-10, 0)-(12, 0), QBColor(8)

Picture2.Line (0, -5)-(0, 25), QBColor(8)

For l = -10 To 20 Step 0.01

y = (A(1, 3) - A(1, 1) * l) / A(1, 2)

Picture2.PSet (l, y)

Y1 = (A(2, 3) - A(2, 1) * l) / A(2, 2)

Picture2.PSet (l, Y1)

Next

End If

u = 2

For r = 1 To n - 1

For j = u To n

q = -A(j, r) / A(r, r)

For i = 1 To n + 1

For t = 1 To n + 1

B(t) = q * A(r, t)

Next t

A(j, i) = A(j, i) + B(i)

Next i

Next j

u = u + 1

Next r

d = A(n, n + 1)

h = 1

For j = 0 To n - 1

x(n - j) = d / A(n - j, n - j)

If (n - j = 1) Then GoTo l1

d = A(n - j - 1, n + 1) - x(n - j) * A(n - (j + 1), n - j)

Next j

l1:

For i = 1 To n

Picture1.Print "x"; i; "="; x(i)

Next

End Sub

6. Результаты выполнения программы.

В качестве проверки возьмем систему двух линейных уравнений, решим ее:

Проверим решение с помощью созданной программы:

Вводим количество уравнений: 2.

Вводим элементы в следующей последовательности (с разбиением чисел косой чертой «/»): коэффициенты первого ряда – a11, a12, b1; коэффициенты второго ряда – a21, a22, b2. Получим в результате строку «-1/1/-1/4/4/20».

При нажатии на кнопку программа строит графики (при n=2) и вычисляет корни системы линейных алгебраических уравнений.

Рис. 4. Вид программы при ее запуске.

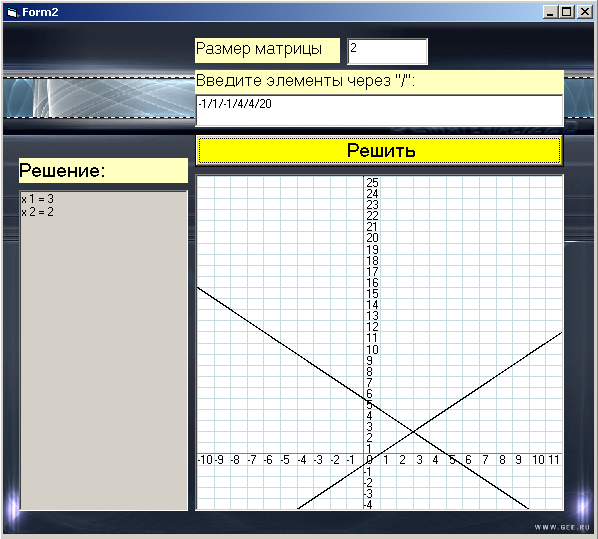
Рис. 5. Вид программы при введении коэффициентов,

и визуализации (n=2).

7. Заключение.

В ходе курсовой работы был собран материал по методу Гаусса решения систем линейных алгебраических уравнений. Далее был составлен алгоритм решения СЛАУ и спроектирована оболочка программа в среде Microsoft Visual Basic 6.0 for 32-bit Windows Development. Решение контрольного примера показало, что программа составлена верно. Для решения данной задачи была прочитана соответствующая литература и справочники - математические и по среде программирования Visual Basic.

8. Список использованной литературы.

1. Ананьев А., Федоров А. «Самоучитель Visual Basic 6.0». БХВ - Петербург, 2005 г. - 346 с.

2. Бронштейн И.Н., Семендяев К.А. Справочник по математике. Для инженеров и учащихся ВТУЗов. Гос. издательство физико-математической литературы. М.: 1962 г. – 608 с.

3. Виленкин Н.Я. Алгебра и математический анализ. Учебное пособие для учащихся школ и классов с углубленным изучением математики. М.: «Просвещение», 1998. – 288 с.

4. Ефимов Н.В. Краткий курс аналитической геометрии. М.: «Академкнига», 1967 – 267 с.

5. Кузьмина Е.А., Минасов Ш.М., Тархов С.В. Электронный лабораторный практикум 

6. по дисциплине: "Информатика". Уфа, кафедра Информатики УГАТУ, 2004-2005 г.

7. Стойлова Л.П. Математика: Учебник для студ. высш. пед. учеб. заведений. М.: «Академия», 1999. – 424 с.

15