
Распределения, связанные с нормальным Нормальное распределение
Нормальное
распределение с математическим ожиданием
![]() и дисперсией
и дисперсией
![]() обозначается
обозначается
![]() .
Его также называют гауссовским
распределением.
.
Его также называют гауссовским
распределением.
Плотность:
 .
.
Нормальное
распределение симметрично относительно
и для него выполняется
![]() .
.
Моменты
нормального распределения:![]() и
и
![]() при целых
при целых
![]() ,
в частности,
,
в частности,
![]() .
.
Коэффициент
асимметрии:![]() .
.
Куртозис
![]() ,
коэффициент эксцесса равен нулю.
,
коэффициент эксцесса равен нулю.
Стандартным
нормальным распределением называется
![]() .
.
Плотность
стандартного нормального распределения:
![]() .
.
Функция
распределения стандартного нормального
распределения:
![]() .
.
Распределение хи-квадрат
Распределение
хи-квадрат с
степенями свободы обозначается
![]() .
.
Плотность:
![]() ,
где
,
где
![]() — гамма-функция и
— гамма-функция и
![]() .
.
![]() ,
если
,
если
![]() .
.
Если
![]() и независимы в совокупности, то
и независимы в совокупности, то
![]() .
.
Если
![]() ,
то
,
то
![]() и
и
![]() .
.
Коэффициент
асимметрии:![]() .
.
Куртозис
![]() ,
коэффициент эксцесса
,
коэффициент эксцесса
![]() .
.
При
больших
распределение хи-квадрат похоже на
![]() .
.
Распределение Стьюдента
Распределение
Стьюдента с
степенями свободы обозначается
![]() .
Его также называют t-распределением.
.
Его также называют t-распределением.
Если
![]() ,
,
![]() и независимы, то
и независимы, то
![]() .
.
Плотность:
![]() .
.
Распределение
Стьюдента симметрично относительно
нуля и
![]() .
.
Математическое
ожидание существует при
![]() и
и
![]() .
.
При
![]() не существует
-го
момента.
не существует
-го
момента.
Дисперсия
существует при
![]() и
и
![]() .
.
Коэффициент
асимметрии существует при
![]() и
.
и
.
Куртозис
существует при
![]() и
и
![]() ,
коэффициент эксцесса
,
коэффициент эксцесса
![]() .
.
При
больших
распределение хи-квадрат похоже на
![]() .
.
Распределение Фишера
Распределение
Фишера с
![]() и
и
![]() степенями свободы обозначается
степенями свободы обозначается
![]() .
Его также называют F-распределением
или распределением Фишера—Снедекора:
.
Его также называют F-распределением
или распределением Фишера—Снедекора:
Если
![]() ,
,
![]() и независимы, то
и независимы, то
![]()
Плотность:
 ,
если
.
,
если
.
, если .
Если
![]() ,
то
,
то
![]() при
при
![]()
![]() при
при
![]()
 при
при
![]()
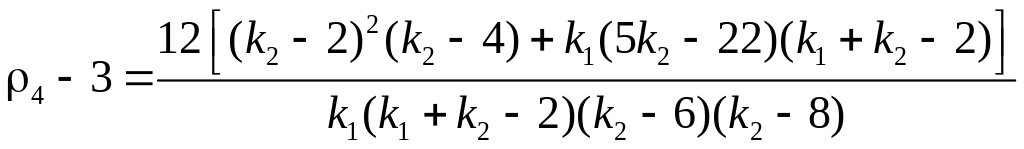 при
при
![]()
