2. Изучение операционного исчисления средствами Mathcad

1.2.1. Cвойство однородности.

Если соответствует изображение , то при заданном действительном или комплексном постоянном a соответствует изображение .

      

1.2.2. Cвойство линейности.

Если функциям и соответствуют изображения и , то при заданных действительных или комплексных констанстах , , ... , линейной комбинации оригиналов

 соответствует линейная комбинация изображений .

      

1.2.3. Свойство подобия.

Если оригиналу соответствует изображение , то при оригиналу соответствует изображение .

Это свойство показывает, каким образом меняется вид изображения при изменении масштаба аргумента оригинала. Например,

          

          

 

1.2.4. Для любого постоянного оригинал имеет изображением .

           

     

 

1.2.5. Дифференцирование оригинала.

Если непрерывна и дифференцируема на [0, ], то дифференцированию оригинала соответствует умножение его изображения на s с вычитанием значения оригинала в нуле.

Можно получить выражения для изображений, соответствующих высшим производным оригинала:

Приведенные формулы указывают путь операторного решения некоторых видов дифференциальных уравнений.

Пример. Преобразование в операторную форму дифференциального уравнения

при начальных условиях , , , и нахождение его частного решения.

           

         

В силу свойства линейности операторное уравнение имеет вид

Его решение относительно функции-изображения:

msgMapleSolve    

Переход к оригиналу дает решение исходного уравнения относительно функции :

 

 

Рис. 2. Графическое представление решения уравнения

 

1.2.6. Интегрирование оригинала.

Интегрированию функции-оригинала соответствует деление изображения на s.

        

 

1.2.7. Интегрирование изображения.

Если интеграл сходится, то он служит изображением функции .

 

1.2.8. Дифференцирование изображения.

Если служит оригиналом для , то служит оригиналом для .

В общем случае служит оригиналом для .

          

 

1.2.9. Теорема смещения изображения.

Если имеет изображением , то для любого справедливо, что имеет изображением .

            

       

 

1.2.10. Теорема запаздывания оригинала .

Если имеет изображением , то для любого справедливо, что имеет изображением .

            

       

 

1.2.11. Теорема опережения оригинала.

Если и имеет изображением , то имеет изображением 

            

 

1.2.12. Теорема о свертке оригиналов (теорема умножения изображений).

Определение. Пусть даны функции , ,определенные на отрезке [0, t]. Сверткой этих функций называется новая функция , определяемая равенством

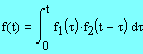
Теорема. Если , имеют своими изображениями соответственно , ,то их свертка имеет изображением произведение .

 

 

1.2.13. Tеорема Дюамеля.

Теорема: Если оригиналы , непрерывно дифференцируемы на [0, ] , имеют своими изображениями соответственно , и сверткой оригиналов является , то   имеет изображением произведение .

Используем определения предыдущего примера.