6.3 Форма звітності з лабораторної роботи:
6.3.1. Тему, мету і порядок виконання роботи.
6.3.2. Результати виконання завдань, проілюстровані графіками та описом ходу виконання завдання.
6.3.3. Оформлені висновки з лабораторної роботи.
6.4 Контрольні запитання
6.4.1. Сформулюйте суть задачі Коші.
6.4.2. Які групи чисельних методів для розв’язання задачі Коші вам відомі?
6.4.3. Що таке крайова задача?
6.4.4. Для чого використовуються функції load, score і sbval?
6.4.5. В чому полягає особливість багатокрокових методів?
6.4.6. Розкрийте суть методів Адамса, Ейлера.
Лабораторна робота №7 розвязок диференціальних рівнянь в частинних похідних
Мета роботи: навчитися розв’язувати диференціальні рівняння в частинних похідних методом кінцевих різниць.
7.1 Основні теоретичні положення
На практиці часто доводиться стикатися з завданнями, в яких шукана величина залежить від декількох змінних. У цьому випадку розв’язоки рівняння містять частинніі похідні і називаються диференціальними рівняннями в частинних похідних. На жаль, дуже багато хто з таких рівнянь не мають аналітичного розв’язку, і щоб розв’язати їх, доводиться вдаватися до чисельних методів. Для розв’язку диференціальних рівнянь в частинних похідних чисельно використовується метод кінцевих різниць.
Метод кінцевих різниць
Чисельне рішення диференціальних рівнянь в частинних похідних методом кінцевих різниць полягає в наступному:
1. Побудова в галузі розв’язку рівномірної сітки, яка містить n вузлових точок (рис.7.1).
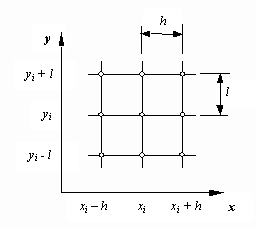
Рисунок 7.1 – Двовимірна сітка
2. Представлення похідних в кінцево-різницеві формі:
,
(7.1)
,
і т.д.
де
- значення
функції f(x,y) в точках
відповідно.
3. Розв’язання отриманої системи з метою отримання наближеного розв’язку у вузлах сітки.
Гіперболічні рівняння в частинних похідних
Найпростішим видом рівняння гіперболічного типу є хвильове рівняння. До дослідження хвильового рівняння призводить розгляд процесів поперечних коливань струни, поздовжніх коливань стержня, електричних коливань в проводі, крутильних коливань валу і т. п.
Розглянемо
одномірне рівняння коливань струни. В
області
потрібно
знайти розв’язок рівняння:
(7.2)
Шукана функція u (x, t) повинна задовольняти початкові умови, що описує початкову (t = 0) форму струни j (x) і швидкість її точок y (x):
,
(7.3)
і граничним умовам, які вказують, що відбувається на кінцях струни (х = 0 і х = 1):
(7.4)
Сукупність початкових і граничних умов називається крайовими умовами.
Для
побудови різницевої схеми розв'язку
задачі (7.2) - (7.4) побудуємо в області
сітку
,
,
,
,
m і
аппроксимуєм рівняння (7.2) у кожному
внутрішньому вузлі сітки на шаблоні
"хрест" (рис.7.2).
Рисунок 7.2 – Шаблон для хвильового рівняння
Використовуючи для апроксимації частинних похідних вираз (7.1), отримуємо наступну різницеву апроксимацію рівняння (7.2):
(7.5)
Розв’язуючи
рівняння (7.6) щодо єдиного невідомого
значення
,
отримуємо наступну схему:
(7.6)
,
Схема
(6) називається тришаровою тому, що
пов'язує між собою значення
функції
u (x, t) на трьох часових шарах з номерами:
j - 1, j, j + 1. Схема (6) є явною, тобто дозволяє
в явному вигляді виразити
через
значення u з попередніх двох шарів.
Для початку розрахунки за схемою (7.6) необхідні значення функції u (x, t) на нульовому (j = 0) і першому (j = 1) часових шарах. Вони визначаються початковими умовами (7.3) і записуються у вигляді:
,
, (7.7)
Граничні умови (4) також записуються в сітковому вигляді:
,
,
(7.8)
Таким
чином, розв’язок вихідної диференціальної
задачі (7.2) - (7.4) зводиться до розв’язання
різницевої задачі (7.6) - (7.8). Схема стійка,
якщо виконана умова Куранта
