Задача Коші

Задачу Коші можна сформулювати таким чином: нехай дано ЗДР:

(6.1)

і початкова умова . Потрібно знайти функцію , яка задовільняє як вказане рівняння, так і початкову умову.

Чисельний розв'язок задачі Коші полягає в побудові таблиці наближених значень розв'язок рівняння в точках . Найчастіше , i = 0, 1, ..., n, де h – крок збільшення змінної x, n - число інтервалів розв’язку з кроком h.

Розглянемо тут дві групи чисельних методів розв’язку задачі Коші: однокрокові і багатокрокових.

Однокрокові методи

Однокрокові методи - це методи, в яких для знаходження наступної точки на кривій y = f (x) потрібна інформація лише про одне в попередньому кроці. Найпростішим з однокрокових методів є метод Ейлера:

(6.2)

Метод Ейлера має невисоку точність (порядку h).

Для досягнення більш високої точності (порядку ) використовують метод Рунге-Кутта четвертого порядку:

, де

, (6.3)

,

Багатокрокові методи

У багатокрокових методах для відшукання наступної точки кривої у = f (x) потрібна інформація більш ніж про одну з попередніх точок.

Нехай знайдено значення в чотирьох послідовних точках. При цьому є також обчислені раніше значення правої частини рівняння (6.1) . Тоді схему методу Адамса можна представити у вигляді:

(6.4)

де кінцеві різниці в точці мають вигляд:

, (6.5)

.

Розв’язок задачі Коші засобами Mathcad

Інструментарій для розв’язоку ЗДР (систем ЗДР) різного порядку в Mathcad представлений широким спектром вбудованих функцій, робота однієї з яких (rkfixed - метод Рунге-Кутта (rk) четвертого порядку з фіксованим (fixed) кроком інтегрування) показана на рис.6.1.

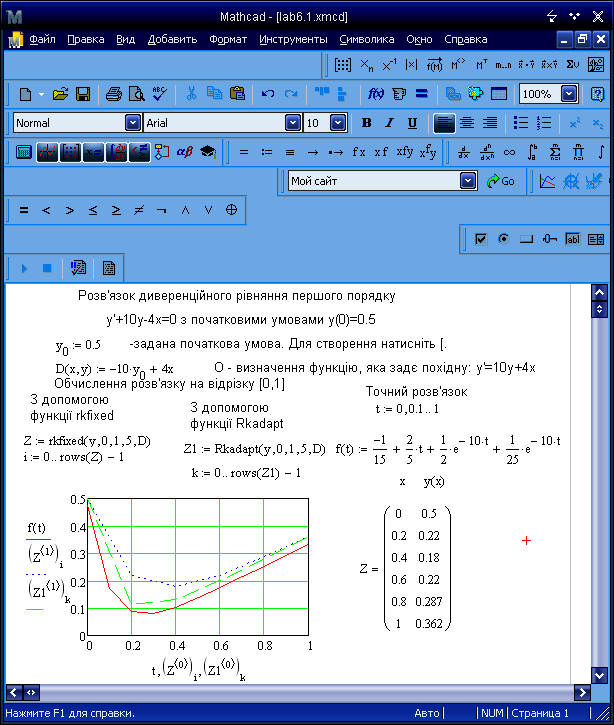
Рисунок 6.1 – Розв’язок ЗДР 1-го порядку

rkfixed(y, a, b, n, D)

Повертає матрицю з р + 1 стовпцями і n + 1 рядками (р - кількість рівнянь або порядок рівняння, n - число кроків на інтервалі [a, b]) - таблиця розв’язків системи: перший стовпець - це значення аргументу х, а наступні стовпці - значення ординат розв’язку. y - вектор початкових умов розмірності n. D (x, y) - функція-вектор з n елементів, що містять перші похідні невідомих функцій.

Можна розв’язати задачу більш точно (більш швидко), якщо зменшити крок h там, де похідна змінюється швидко, і збільшити крок там, де вона веде себе більш спокійно. Для цього передбачена функція Rkadapt (adaption - адаптація). Аргументи і матриця, повернена функцією Rkadapt, так, як при rkfixed (див.рис.6.1). Розв’язок системи ЗДР показано на рис. 6.3 (приклад 2).

Крайові задачі

Крайова задача формулюється таким чином: нехай на відрізку [a, b] потрібно знайти розв’язок диференціального рівняння (для простоти викладеного будемо вести на прикладі ЗДР другого порядку):

(6.6)

при граничних умовах у (а) = А, у (b) = В.

У цьому випадку Mathcad пропонує використовувати функцію sbval, щоб знайти недостатні початкові умови в точці а.

У цьому випадку Mathcad пропонує використовувати функцію sbval, щоб знайти відсутні початкові умови в точці а.

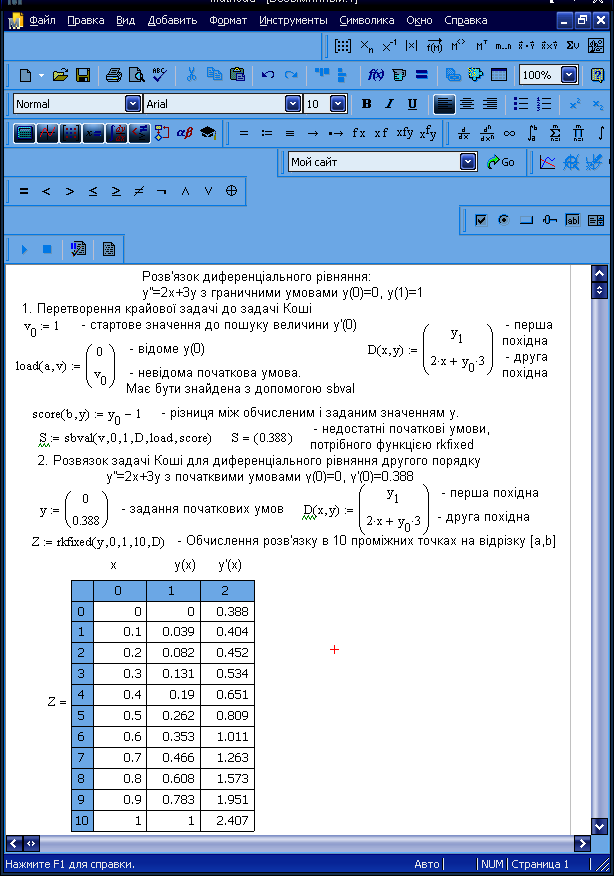
Рисунок 6.2 – Розв’язок крайової задачі

Sbval(v, а, b, D, load, score)

Повертає вектор, що містить відсутні початкові умови в точці а. Вектор v задає початкові наближення, а, b - граничні точки інтервалу розв’язку, D (x, y) - функція-вектор з першими похідними невідомих функцій. load (а, v) - функція-вектор, що повертає значення початкових умов в точці а. score (b, y) - функція-вектор, кожен елемент якого містить різницю між початковою умовою заданою в точці b, і значенням шуканого розв’язку в цій точці.

Після того, як ці недостатні початкові умови будуть отримані, можна розв’язувати звичайну задачу з початковими умовами - задачу Коші, використовуючи будь-яку з функцій, описаних вище (рис.6.1). Приклад розв'язку крайової задачі показаний на рис.6.2.