Ужгородський Національний університет

Інженерно-технічний факультет

кафедра приладобудування

Тягур ю.І.

Задачі з фізики для студентів 2 курсу (3 семестр) інженерно-технічного факультету УжНУ

Ужгород – 2005

Тема 1. Механічні коливання та хвилі Задача 1.1

Кожне конкретне вільне гармонічне коливання, яке описується рівнянням:

,

характеризується значенням амплітуди А і значенням початкової фази . Визначити ці параметри для даного рівняння коливань із початкових умов, тобто коли , .

Розв’язування 1.1

Маючи рівняння

, (1)

Знайдемо залежність :

(2)

Покладемо в рівняннях (1) і (2) і знайдемо:

, (3)

(4)

З рівнянь (3) і (4) знайдемо А:

(6)

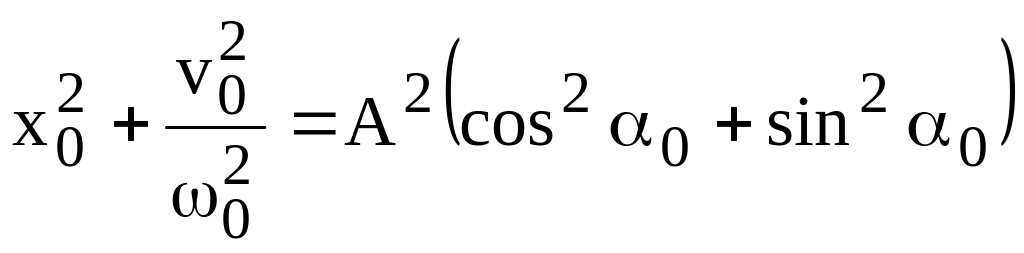(7)

(7)

Враховуючи, що , одержимо:

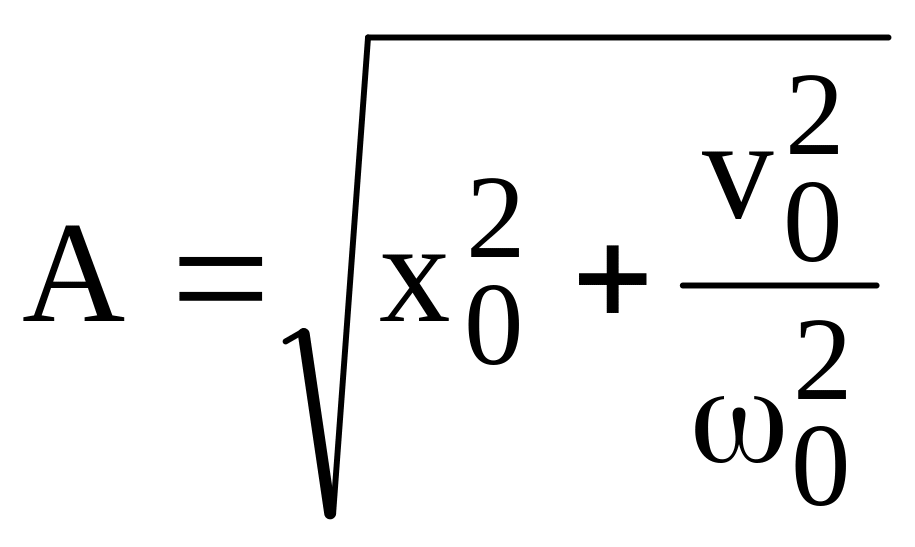(8)

З формул (3) і (4) визначимо

(9)

(10)

(11)

Задача 1.2

Коливання вантажу на пружині масою кг описується рівнянням . Визначити:

1. Амплітуду коливання ;

2. Колову частоту ;

3. Частоту ;

4. Період ;

5. Початкову фазу ;

6. Повну енергію ;

7. Максимальну швидкість руху вантажу ;

8. Коефіцієнт жорсткості пружини .

Розв’язування 1.2

При гармонічних коливаннях рівняння коливань у загальному випадку записується так:

(1)

де – амплітуда коливання; – фаза коливання; – початкова фаза коливання; – циклічна частота; – час від початкового моменту.

Тоді згідно умови розв’язком задачі є:

1. Амплітуда коливання =0,1 м.

2. Колова частота .

3. Частоту визначаємо з рівняння . Звідси [Гц].

4. Період . Тоді, знаючи з п.3 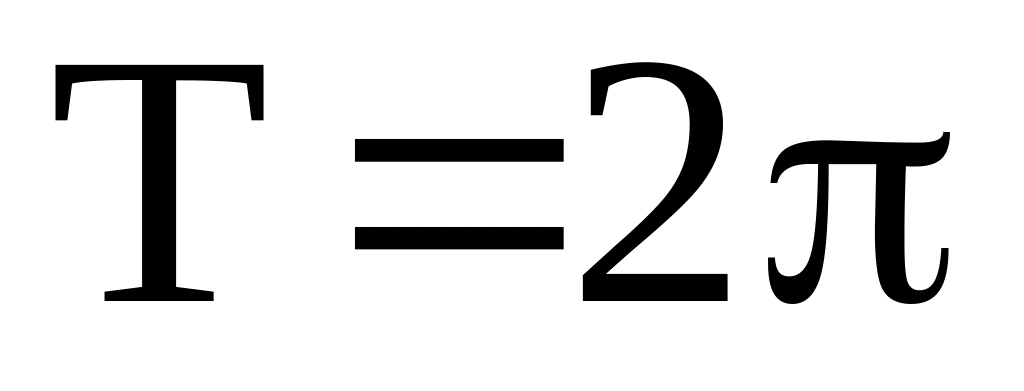[c].

5. .

6. Повна енергія складається із потенціальної і кінетичної . В процесі коливання проходить перетворення кінетичної енергії в потенціальну і зворотній процес. Причому в момент найбільшого відхилення від положення рівноваги повна енергія складається тільки із потенціальної енергії, яка досягає свого максимального значення . А при проходженні системи через положення рівноваги повна енергія складається лише з кінетичної енергії, яка в цей момент досягає найбільшого значення .

Значить повна енергія для нашого випадку слідуюча:

7. Максимальна швидкість руху вантажу :

.

8. Коефіцієнт жорсткості пружини знаходимо з порівняння максимальних значень кінетичної і потенціальної енергій:

; ;

.