Розв’язування

Незалежно від властивостей пластинки її температура встановиться тоді, коли потік випромінювання , що витікає з нагрітої пластинки, стане рівним потоку випромінювання Сонця:

(1)

1. Якщо пластинка має властивості абсолютно чорного тіла, то вона поглинає весь падаючий на неї потік випромінювання. Тому на основі формули (1) задачі №3, маємо:

(2)

де – площа поверхні пластинки, яка повернута до Сонця.

Потік випромінювання знаходимо, застосувавши закон Стефана-Больцмана, враховуючи, що випромінювання витікає з обох сторін пластинки.

(3)

З формул (1)–(3) знаходимо:

(4)

Звідки

К. (5)

2. Не будучи абсолютно чорним тілом, пластинка буде поглинати і випромінювати менше енергії, ніж в першому випадку. Тому зараз замість (4) запишемо:

, (6)

де – коефіцієнт поглинання;

– коефіцієнт випромінювання.

Відомо, що для сірого тіла = .

(7)

(8)

(9)

Відомо, що

(10)

(11)

З цього слідує, що для сірого тіла

, (12)

для всіх частот. Виносячи та за знак інтеграла і скоротивши, прийдемо до відповіді:

(13)

Або

(14)

Таким чином, рівняння (13) приводить до результату, який записаний рівнянням (4) для абсолютно чорного тіла, тобто температура сірої і чорної пластинки будуть однакові.

3. Для загального випадку нечорного тіла, яке має вибіркове поглинання, умова (12) не виконується. В цьому випадку коефіцієнт поглинання залежить не тільки від властивостей і температури пластинки, але і від розподілу енергії у спектрі Сонця. Тому 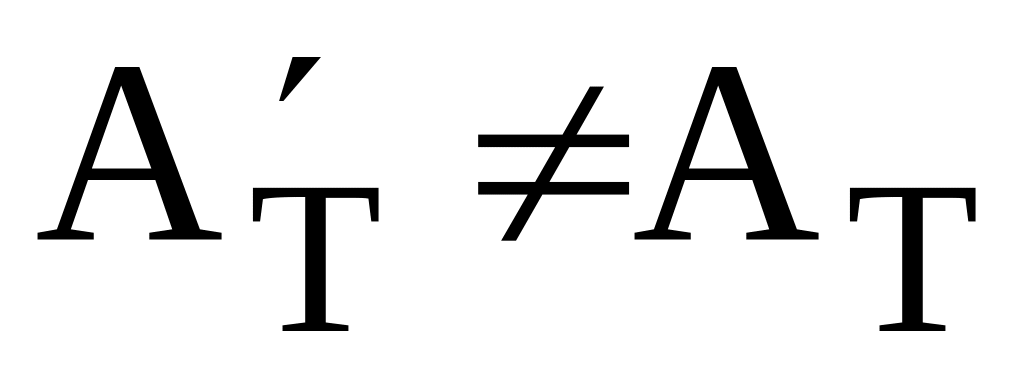і температура нечорного тіла не рівна температурі абсолютно чорного тіла. Знак нерівності не залежить від того, до якої частини сонячного спектру належить випромінювання, яке переважно поглинається пластинкою. Найбільшою буде температура пластинки в тому випадку, коли це випромінювання відноситься до інтервалу частот, який відповідає найбільшому значенню спектральної густини енергетичної світності Сонця.

Значить, для реального тіла потрібно, щоб було максимальним для мкм.

Задача 5 (26–5 Фирганг)

Виходячи із співвідношень:

(1)

де

(2)

та

(3)

знайти співвідношення між величинами та , які характеризують спектральну густину енергетичної світності тіла. Записати формулу Планка для величини .