Задача 3.4.

Маємо послідовно з’єднані резистор опором =3,9 кОм і конденсатор ємністю =0,25 мкФ. Визначити вказані нижче параметри цієї ділянки кола при струмі промислової частоти ( =50 Гц):

(Відповідь: =40 Гн).

1. Ємнісний опір кола ( );

2. Повний (комплексний) опір ( );

3. Коефіцієнт потужності ( );

4. Зсув фаз між силою струму і напругою;

5. Якої індуктивності котушку треба приєднати послідовно з резистором ( ) і конденсатором ( ), щоб в колі спостерігався резонанс?

Розв’язування 3.4

1. ; =12740 Ом.

2. ; =13,3 Ом.

3. ; =3,9 кОм / 13,3 кОм = 0,3.

4. =0,3; =72^О; =0,4 .

5. Повний опір кола змінного струму визначається за формулою 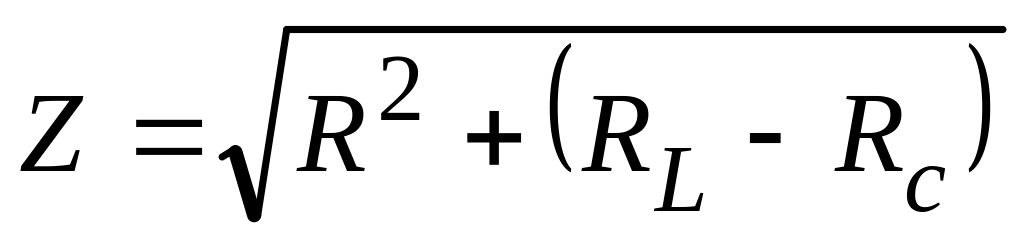. При резонансі . Звідси можна знайти індуктивність потрібної котушки:

; ;

=40 Г.

Задача 3.5

Період електричних коливань в антені радіопередавача дорівнює сек. Визначити частоту коливань і довжину електромагнітної хвилі.

Розв’язування 3.5

1. Гц.

2. ; ; м.

Задача 3.6

Маємо схему електричного кола (див. рис.) для спостереження затухаючих коливань в коливальному контурі, а також електронний осцилограф.

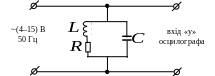
Рис. до задачі 3.6

1. Пояснити принцип одержання осцилограми затухаючих коливань за допомогою даної установки.

2. Встановити, чи залежить період затухаючих коливань від їх амплітуди: – ?

3. Визначити період ( ), частоту ( ) та колову частоту ( ) коливань, якщо кількість коливань на осцилограмі .

4. Якою формулою визначається індуктивність котушки ( ) даного коливального контуру.

5. На яку довжину хвилі настроєно даний контур ( )?

6. Визначити логарифмічний декремент затухання коливань ( ).

7. Визначити коефіцієнт затухання коливань ( ).

8. Визначити сталу часу ( ).

9. Визначити активний опір контуру ( ).

10. Визначити хвильовий опір контуру ( ).

11. Визначити затухання контуру ( ).

12. Визначити добротність контуру ( ).

13. Побудувати графіки залежності та , якщо змінюється від 1 до 400 пФ.

14. Побудувати графік при умові 13.

Розв’язування 3.6

1. Коливання, які можна побачити на екрані осцилографа утворюються так. До коливального контуру через діод ( ) проходять імпульси струму тривалістю 1/100 секунд, тому що це є час одного півперіоду змінного струму промислової частоти 50 Гц:

; сек; сек.

У цей час конденсатор контуру заряджається. У наступний півперіод струм у контур не надходить і протягом цього півперіоду (0,01 с) на екрані можна спостерігати осцилограму затухаючих коливань, які відбуваються у коливальному контурі. Оскільки нас цікавлять лише затухаючі коливання, то за допомогою ручок керування осцилографом ми їх дістанемо на екрані. Час ( ) цих коливань дорівнює 0,01 сек.

2. Встановити, чи залежить період ( ) від амплітуди ( ), можна вимірявши по осі абсцис відрізки, які відповідають періодам коливань з різними амплітудами. Можна зробити висновок, що виявити помітної залежності періоду коливань від їх амплітуди не можна. Це означає, що періоди виявляються однаковими.

3. Враховуючи, що інтервал часу ( ), протягом якого відбуваються коливання, дорівнює 0,01 сек, а також те, що кількість коливань , визначаємо період коливань:

; с.

• Частота коливань ( ) (кількість коливань за одиницю часу): ; =1/0,001 с = 1000 Гц.

• Колова частота ( ) показує число коливань за секунд: ; =2^.3,14^.1000 с^-1=6280 с^-1.