Фгбоу впо национальный исследовательский университет

МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ

КАФЕДРА ТЕОРЕТИЧЕСКИХ ОСНОВ ЭЛЕКТРОТЕХНИКИ

Лабораторная работа № 3 Моделирование длинной линии однородной цепной схемой

Выполнил:
Группа:
Проверил:

Москва 2012 Лабораторная работа № 3 Моделирование длинной линии однородной цепной схемой

Цель работы – исследование электромагнитных процессов в длинной линии методами физического моделирования, сравнение результатов физического моделирования с результатами расчета по аналитическому описанию процессов в линии.

Ключевые слова: длинная линия, однородная цепная схема, четырехполюсник, каскадное соединение, низкочастотный фильтр, физическая модель.

Объект и задача моделирования

Объект исследования: однородная длинная линия при синусоидальных токах и напряжениях и различных нагрузках.

Задача моделирования: Под задачей физического моделирования в данной работе понимается, во-первых, исследование искусственного физического объекта – модели линии, в виде однородной цепной схемы из П-образных четырехполюсников. Процессы в модели имеют другую физическую природу, но математически они подчиняются тем же закономерностям, что и процессы в реальной линии, а их исследование не вызывает сложностей. И, во-вторых, проведение экспериментального исследования модели с переносом его результатов на объект моделирования.

Теоретическая справка Аналитическое описание процессов в длинной линии

Распределение напряжений и токов в однородной длинной линии без потерь (рис.1) описывается уравнениями:

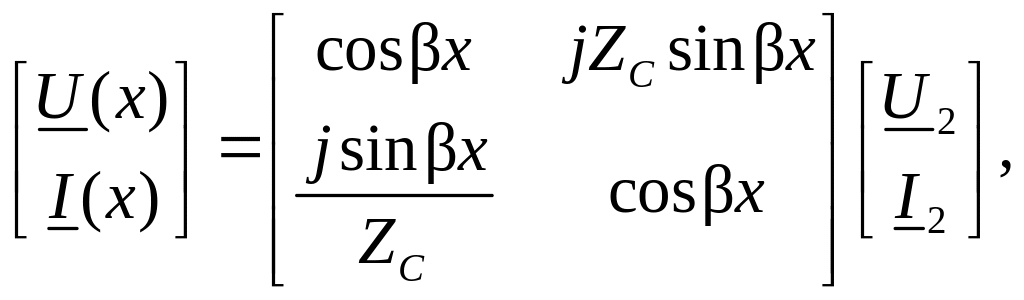(1)

где: х – расстояние от конца линии до точки наблюдения процесса (при х=l ), Z_C – волновое (характеристическое) сопротивление линии:

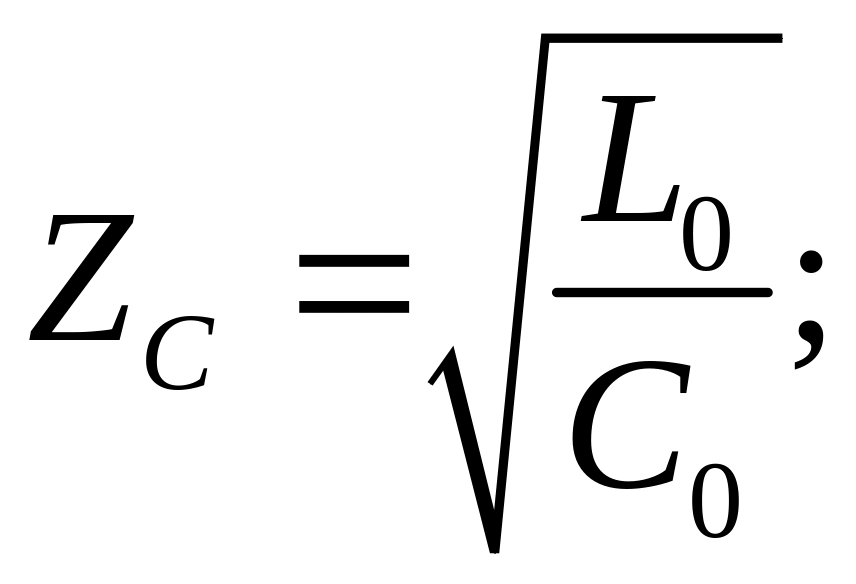(2)

β – коэффициент фазы:

(3)

позволяющий определить длину волны в линии:

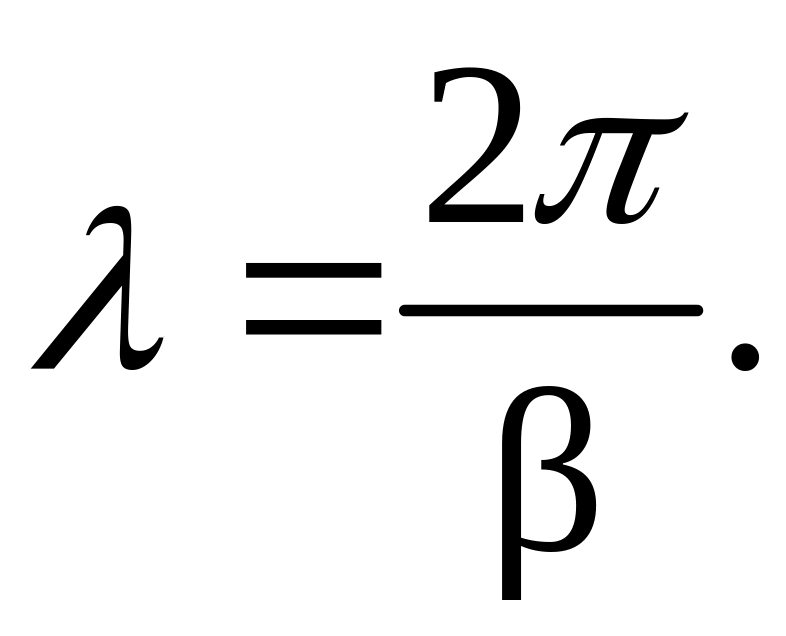(4)

Здесь - угловая частота синусоидальных токов и напряжений, погонная индуктивность L₀ и погонная емкость C₀ – первичные параметры линии. Волновое сопротивление Z_C и коэффициент распределения - вторичные параметры линии (для линии без потерь коэффициент затухания и ).

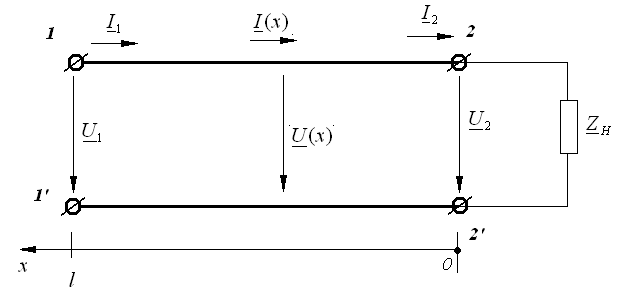
Рис.1

Уравнения (1) позволяют построить графики распределения действующих значений тока и напряжения вдоль линии для различных режимов нагрузки. В частности, при согласованной нагрузке

и

и

т.е. модули действующих значений напряжения и тока не зависят от х, а начальная фаза напряжения (тока) изменяется пропорционально х. При согласованной нагрузке в линии существует только прямая волна. Согласованный режим линии называется режимом бегущей волны.

При коротком замыкании холостом ходе и реактивной нагрузке в линии распространяются прямая и обратная волны равной амплитуды.

Для иллюстрации режима стоячих волн, рассмотрим распределенияU(x) и I(x) при холостом ходе и емкостной нагрузке.

При холостом ходе, когда I₂=0, имеем

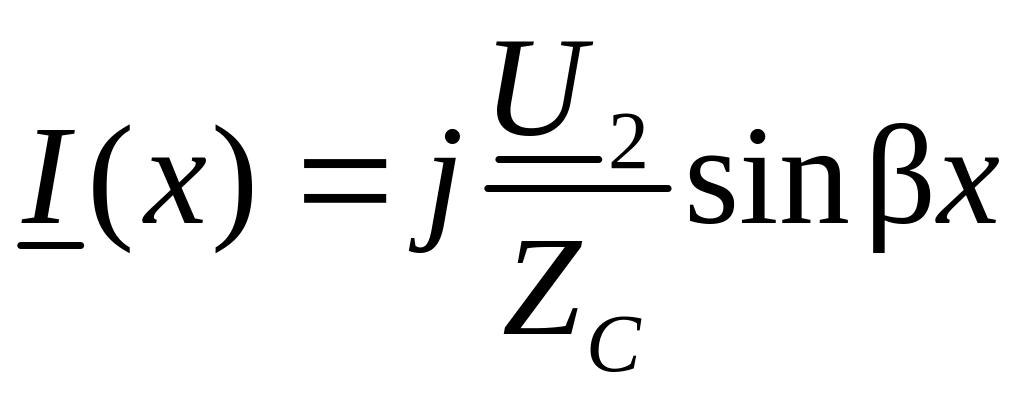и

и

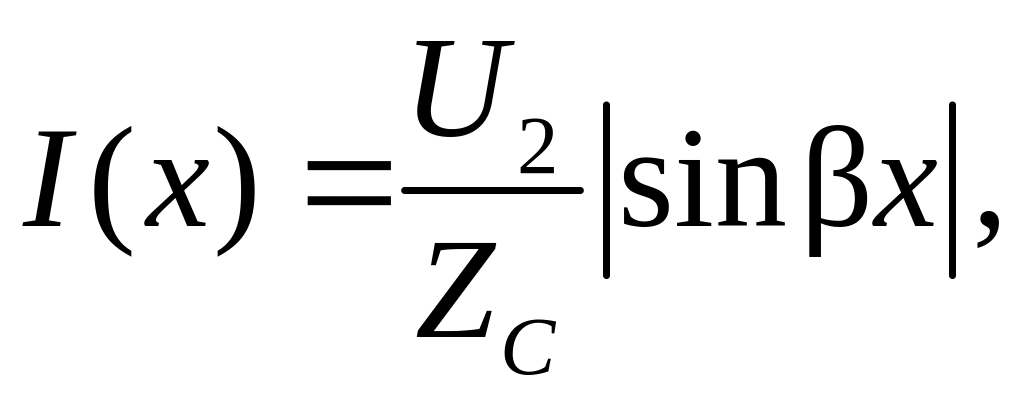
т.е. действующие значения U и I изменяются вдоль линии по закону «выпрямленной» синусоиды, а начальная фаза напряжения (тока) в пределах половины длины волны остается неизменной и при переходе через узел скачком меняется на π. Такой режим называется режимом «стоячих волн». В конце линии - пучность напряжения и узел тока.

При емкостной нагрузке будем иметь

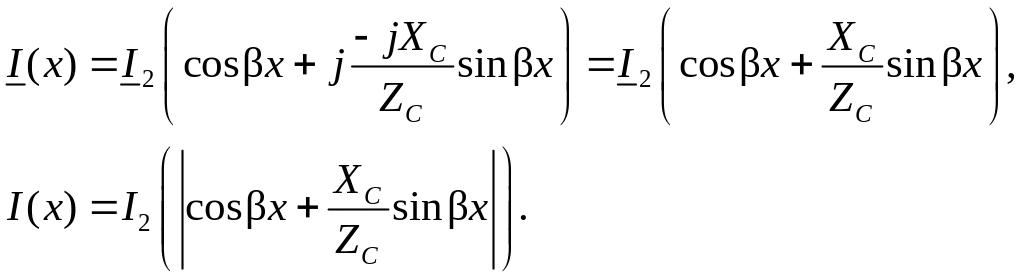
Таким образом при емкостной нагрузке также наблюдается режим «стоячих волн», но в отличие от режима холостого хода в конце линии не будет максимума напряжения. При перемещении от конца линии к началу на расстоянии будет узел напряжения, где y можно найти из уравнения