
- •Многоэлектронный атом
- •Лекция 2
- •2 Приближения
- •Среди состояний с одной двухэлектронной конфигурацией наименьшей энергией обладает состояние с наибольшей мультиплетностью.
- •Среди состояний с одной двухэлектронной конфигурацией и мультиплетностью наименьшей энергией обладает состояние с наибольшим l
- •Лекция 3
- •Строение молекул
- •Атом водорода
- •Лекция 4
- •Лекция 5
Лекция 4
Многоатомные молекулы
Необходимо знать геометрию молекулы.
Это делается с помощью построения поверхности потенциальной энергии (ППЭ) – функция энергии от межъядерного расстояния.

Решаем много
раз для разных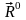 ,
где минимумы, там и геометрия.
,
где минимумы, там и геометрия.

Проще – теория ОЭПВО (полезно для d-элементом)
метан – AX4 – тетраэдр
аммиак – AX3E – псевдотетраэдр (треугольная пирамида)
вода– AX2E2 – угловая
Орбитали многоатомных молекул характеризуются точечной симметрией, в зависимости от точечной группы, к которой относится молекула.
Если молекула имеет более чем 1 ориентаций в пространстве, неотличимых от исходных, то она обладает симметрией.
Перевод молекулы из исходной ориентации в другую неотличимую называется операцией симметрии.
Элемент симметрии – ось, точка, или плоскость , отн. которых выполняется операция симметрии.
Точечная симметрия – симметрия, в которой при выполнении операций сохраняется положение 1 точки – центра тяжести.
Элементов симметрии в точечной гр. симметрии 5.
Ось симметрии n-го порядка Сn – если через молекулу можно провести ось, при повороте вокруг которой на угол
 молекула
совмещается с исходной, то говорят, что
молекула имеет ось симметрии n
– го порядка.
молекула
совмещается с исходной, то говорят, что
молекула имеет ось симметрии n
– го порядка.
Ось наивысшего порядка – главная ось.
Плоскость симметрии , - если через молекулу можно провести плоскость, которая делит ее на 2 половины, каждая из которых является зеркальным отражением другой, то говорят что у молекулы есть плоскость симметрии.
3 вида плоскостей
вертикальная - v проходит через главную ось симметрии
горизонтальная H – перпендикулярно главной ось симметрии
диэдрические d – делит пополам угол, которых образуют между собой оси симметрии
Зеркально-поворотная ось n-го порядка.
Sn – если через молекулу провести ось, при повороте вокруг которой на угол и последующем отражении в плоскости перпендикулярной этой оси, молекула принемает ориентацию, неотличимую от исходной, то она имеет зеркально поворотную ось n-го порядка
центр инверсии , i – если у молекулы имеется точка, обладающая следующими свойствами: если через нее и любой атом провести линию, то с другой стороны на том же расстоянии от этой точки встретится такой же атом, то молекула обладает центром инверсии.
Идентичность, Е – ничего
Точечная группа – совокупность операций симметрии, которая может быть проведена с этой молекулой при условиях:
последовательное выполнение двух операций симметрии должно давать тот же результат, как выполнение третьей, которая входит в группу. А*В=С
выполнение операций симметрии подчинены ассоциативному закону умножения А*(В*С)=(А*В)*С
каждая операция симметрии должна соответствовать обратной операции, входящей в данную группу, возвращающей молекулу в исходное состояние
А*А-1=Е
идентичность должна быть в наборе операций
Обозначения по Шенфлиссу
С –молекула имеет 1 ось симметрии
D – несколько осей симметрии (исключения – тераэдр Тd, октаэдр Oh, икосаэдр Ih)
C1 – нет элементов симметрии
СS – есть только плоскость симметрии
 - С2V
- С2V
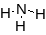 - C3V
- C3V
 - D2h
- D2h
 - D6h
- D6h
