Лабораторная работа № 12 Тема: «Исследование рекурсивных и итерационных алгоритмов»

Цель работы – изучить принцип построения рекурсивных и итерационных алгоритмов.

Теоретические сведения

12.1 Рекурсия

Рекурсия — это такой способ организации вспомогательного алгоритма (подпрограммы), при котором эта подпрограмма (процедура или функция) в ходе выполнения ее операторов обращается сама к себе. Вообще, рекурсивным называется любой объект, который частично определяется через самого себя. Если подпрограмма Р вызывает себя в своем теле, то такая рекурсия называется прямой, если же подпрограмма Р вызывает подпрограмму Q, которая прямо или косвенно вызывает Р, то такая рекурсия называется косвенной. Рекурсией также называют процесс выполнения рекурсивной подпрограммы.

Классическим примером рекурсивной функции является функция вычисления факториала. Для того чтобы получить значение факториала числа n, требуется умножить на n факториал числа (n – 1).

На рис.12.1 показана блок схема алгоритма подпрограммы, которая производит рекурсивное зацикливание: будет выводиться значение «1», после чего подпрограмма снова будет вызывать себя и т.д. до бесконечности. Поскольку при каждом вызове подпрограммы в программный стек помещается ее запись активации, то, в конце концов, программный стек переполнится, и программа завершится с ошибкой. Таким образом, чтобы рекурсия завершалась, необходимо, чтобы рекурсивный вызов происходил не всегда, а лишь при выполнении некоторого условия.

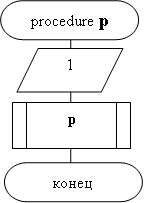
Рисунок 12.1 – Пример подпрограммы с рекурсивным зацикливанием

Рассмотрим рекурсивные подпрограммы рис.12.2.

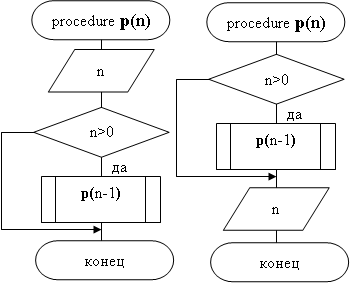
а) б)

Рисунок 12.2 – Примеры подпрограмм с применением рекурсии

При вызове процедуры p(5) рис.12.2а выводится значение «5», вызывается процедура p(4); затем выводится «4» и вызовется p(3) и т.д. до вызова p(0), когда выводится «0» и, поскольку условие n>0 станет ложным, рекурсия завершится. Итак, в результате вызова p(5) на экран будет выведено «5 4 3 2 1 0».

При вызове подпрограммы p(5) рис.12.2б вначале проверится условие n>0 и, поскольку оно истинно, вызовется p(4), затем p(3) и т.д. до p(0). Так как при вызове p(0) условие n>0 уже не выполняется, то осуществится вывод 0 и произойдет выход из вызова p(0) в вызов p(1) сразу после условного оператора. Далее осуществится вывод «1» и выход из вызова p(1). В результате на экран будет выведено «0 1 2 3 4 5». Процесс возврата из уже сделанных рекурсивных вызовов продолжится, пока не будет осуществлен выход из вызова p(5).

Схема рекурсивных вызовов подпрограмм на рис.12.2 изображена на рис.12.3:

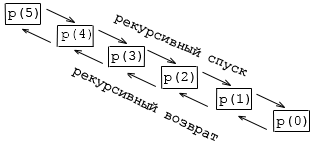
Рисунок 12.3 – Схема рекурсивных вызовов спуска и возврата

Процесс рекурсивных вызовов называется рекурсивным спуском, а процесс возврата из них – рекурсивным возвратом. Глубиной рекурсии называется максимальное число вложенных рекурсивных вызовов (в нашем примере глубина рекурсии равна 5). Число вложенных рекурсивных вызовов в данный момент выполнения программы называется текущим уровнем рекурсии.

Несколько замечаний, относительно целесообразности применения рекурсивных подпрограмм:

1. Рекурсивные алгоритмы являются эффективным средством программирования для некоторого класса задач: сложные задачи численного анализа, комбинаторики, алгоритмов трансляции, операций над списковыми структурами и т. д. Программы в этом случае имеют небольшие объемы по сравне­нию с итерацией и требуют меньше времени на отладку.

2. При каждом рекурсивном вызове на программный стек помещается запись активации подпрограммы. Поэтому если количество рекурсивных вызовов большое или локальные переменные рекурсивной процедуры имеют большой размер, то программный стек может переполниться и возникнет ошибка времени выполнения программы.

3. Накладные расходы на рекурсивные вызовы достаточно велики, поэтому если есть явное нерекурсивное решение, то следует предпочесть его.

4. Можно доказать, что любая прямая рекурсия может быть заменена итерацией.