
- •Раздел 10. Кратные интегралы. §. Начальные понятия и определения
- •§. Определение кратного интеграла
- •§. Свойства кратных интегралов.
- •§. Замена переменных в кратных интегралах.
- •§. Криволинейные интегралы 1го рода.
- •§. Криволинейные интегралы 2го рода.
- •§. Условия независимости криволинейного интеграла 2го рода от пути интегрирования.
- •Если u(X, y, z) такая, что ,
- •§. Задача о нахождении площади поверхности.
- •§ . Поверхностные интегралы 2 рода.
- •§. Скалярные поля.
- •§. Векторные поля.
- •§. Теорема Гаусса-Остроградского.
- •§. Теорема Стокса.
- •§. Задача о движении твердого тела.
- •§. Оператор гамильтона – оператор «набла»
§. Теорема Гаусса-Остроградского.
П
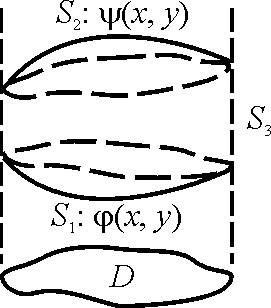
![]() области
области
![]() заданы функции
заданы функции
![]() непрерывные на
вместе со своими производными
непрерывные на
вместе со своими производными
![]() .
Тогда:
.
Тогда:![]()
![]() .
.
При
этом, поверхность
ориентирована наружу области
![]() .
.
∆.
а) Рассмотрим
![]() :
:
![]()
![]() .
.
Здесь
учтено, что
![]() т.к.
т.к.
![]() .
Получено, что
.
Получено, что
![]() .
.
б) и в) получаются аналогично:
![]() ,
,
![]() .
.
Складывая три полученные формулы, получим формулу Гаусса-Остроградского. ▲
Def:
Величина
![]() для векторного поля
для векторного поля
![]() называется дивергенцией векторного
поля:
называется дивергенцией векторного
поля:
![]() ,
,
и
теперь формулу Гаусса-Остроградского
можно записать так:
![]() .
.
*.
Рассмотрим в
точку
![]() и
и
![]() – сферу радиуса
– сферу радиуса
![]() с центром в точке
.
Найдем:
с центром в точке
.
Найдем:
 .
.
(Здесь, по ходу преобразований была применена теорема о среднем).
Следовательно:
 ,
,
т.е.
дивергенция векторного поля
![]() есть мощность источника силовых линий
поля
,
расположенного в точке
.
Это, инвариантное относительно системы
координат, определение дивергенции.
есть мощность источника силовых линий
поля
,
расположенного в точке
.
Это, инвариантное относительно системы
координат, определение дивергенции.
И теорема Гаусса-Остроградского может быть сформулирована так, что будет ясен ее физический смысл:
Поток векторного поля через замкнутую поверхность равен суммарной мощности источников векторного поля расположенных внутри области.
Дивергенция – еще одна, скалярная, характеристика векторного поля.
§. Теорема Стокса.
Пусть
в
заданы функции
,
непрерывные вместе со своими первыми
производными
![]() Пусть
Пусть
![]() замкнутый контур в
замкнутый контур в
![]() ,
а
,
а
![]() –поверхность в
натянутая на контур
,
причем
–поверхность в
натянутая на контур
,
причем
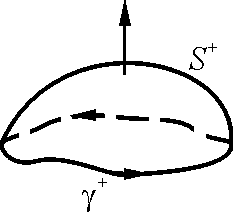
![]() одинаково взаимно ориентированы. Тогда:
одинаково взаимно ориентированы. Тогда:

=
 =
=
=
 .
.
∆.
Интеграл
![]() по замкнутому контуру называется
циркуляцией векторного поля.
по замкнутому контуру называется
циркуляцией векторного поля.
а).
Пусть
![]() .
.
![]()
![]()
![]()


б), в) Аналогично:
![]() ,
,
![]() .
.
Суммируя полученные три формулы, получаем формулу Стокса. ▲.
D
![]() называется ротором векторного поля
.
называется ротором векторного поля
.
![]() ,
,
и
тогда формула Стокса запишется так:
![]() .
.
Рассмотрим
,
и
![]() ,
найдем:
,
найдем:
 следовательно:
следовательно:

Получили
инвариантное относительно системы
координат определение
![]() :
:
Проекция ротора векторного поля на вектор нормали к поверхности определяется пределом отношения циркуляции вдоль замкнутого контура к мере поверхности ограниченной данным контуром, когда контур стягивается в точку. И теорема Стокса:
Циркуляция векторного поля вдоль контура есть сумма циркуляций поля в точках расположенных на поверхности , краем которой является контур .
§. Задача о движении твердого тела.
Пусть
твердое тело движется по закону:
![]() ,
где
,
где
![]() .
Запишем
.
Запишем
 ,
и тогда:
,
и тогда:
![]() ,
,
![]() ,
,
![]() .
.
П

 т.е.
т.е.
![]() .
Этот пример объясняет термин «ротор
поля» или «вихрь поля» или «вращение
поля».
.
Этот пример объясняет термин «ротор
поля» или «вихрь поля» или «вращение
поля».
Примеры:
1.
![]() .
.
2.
 .
.
3.

![]()
![]()


4.
Вычислить
![]() по внешней стороне конуса
по внешней стороне конуса
![]() с крышкой
.
с крышкой
.
Применяя формулу Гаусса – Остроградского, получаем:

