§ . Поверхностные интегралы 2 рода.

Пусть в Е₃ задана поверхность : ;

, и на поверхности S задана вектор-функция

и, при этом .

Рассмотрим: .

Если такой предел существует и конечен, то он называется поверхностным интегралом 2-го рода и обозначается .

Физический смысл поверхностного интеграла 2-го рода – поток векторного поля через поверхность S в направлении нормали, определяемой вектором , т.е. стороной поверхности. Собственно говоря, это и есть определение потока векторного поля через поверхность.

Свойства поверхностного интеграла 2-го рода:

1. Интеграл меняет знак при изменении стороны поверхности, по которой идет интегрирование: .

2. Связь с поверхностным интегралом 1 рода.

.

Здесь единичный вектор нормали к поверхности; – направляющие косинусы нормали к поверхности; , , ;

.

3. Если помнить о том, что: ,

, , легко написать формулу для вычисления поверхностного интеграла 2-го рода

.

Примеры вычисления поверхностных интегралов 2 рода.

1. Вычислить , где S – внешняя сторона сферы =

Вектор нормали был найден в предыдущем параграфе, в примере 3.

.

Знак в выражении для берем так, чтобы в 1 октанте координаты вектора были положительными (внешняя сторона).

.

Вектор .

Тогда: =

= . ▲

2. Вычислить , если S- внешняя сторона конуса

с крышкой z = 1.

Δ Поверхность интегрирования состоит из двух частей – боковой поверхности конуса и крышки. Поэтому: .

а). Для вычисления первого из них, отметим что и, следовательно:

.

б). Для вычисления второго из них, вспомним что для поверхности, заданной явно: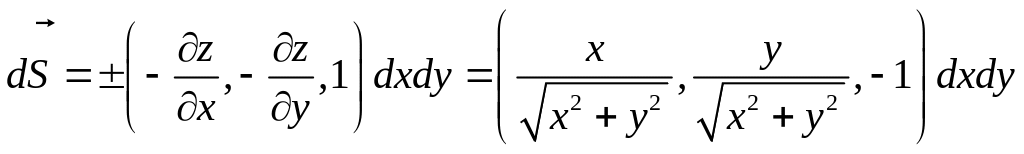 . Знак выбран так, чтобы получить внешнюю нормаль к поверхности. Получаем:

.

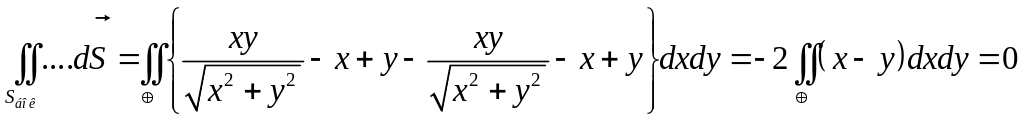Таким образом .

§. Скалярные поля.

П

усть задана область в евклидовом пространстве и в задана функция . Тогда говорят, что в задано скалярное поле (синоним: функция трех переменных). Поверхности называются поверхностями уровня скалярного поля.

Пусть задан вектор с известными направляющими косинусами .

Производной скалярного поля по направлению называется величина:

.

Запишем параметрическое уравнение прямой :

;

Тогда на этой прямой:

и тогда:

.

Вводя вектор получим: .

Из делаем вывод, что вектор указывает направление максимального роста поля и по величине равен скорости роста поля в этом направлении.

Такое определение является инвариантным относительно системы координат.

Если для векторного поля существует скалярное поле такое, что то поле называется потенциальным полем а скалярное поле называется его потенциалом.

Необходимое и достаточное условие потенциальности поля :

.

§. Векторные поля.

Пусть задана область в евклидовом пространстве , и в задана векторная функция . Тогда, говорят что в задано векторное поле.

Def: Линии в пространстве в каждой точке которых векторное поле направлено по касательной к данной линии называется векторными линиями поля (силовыми линиями, линиями тока).

Векторные линии можно найти исходя из системы дифференциальных уравнений векторных линий: , например для :  – прямые, проходящие через начало координат.