Если u(X, y, z) такая, что ,

то ,  ;

 ;  ^.

Замечание 3. В случае независимости криволинейного интеграла от пути

интегрирования, U(x, y, z) такая что:

.

Физики называют функцию U(x, y, z) потенциалом векторного поля , а поле F – потенциальным – “ Работа равна разности потенциалов”.

Математики называют функцию U(x, y, z) первообразной для Pdx+Qdy+Rdz –

интеграл равен разности первообразных в конце и начале пути.

Примеры:

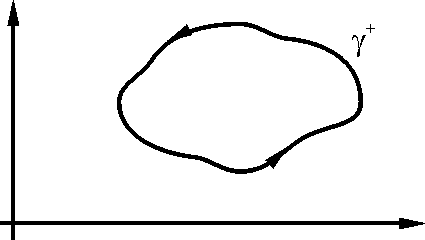
1⁰. Вычислить для различных контуров γ.

а). Пусть контур γ ограничивающий область G таков, что не содержит т. (0,0). Для вычисления интеграла воспользуемся формулой Грина.

где,

, , , .

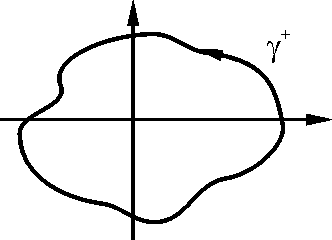
б). Пусть контур γ⁺ окружает точку (0,0). В этом случае нельзя применить формулу Грина ибо и в точке (0,0) не существуют.

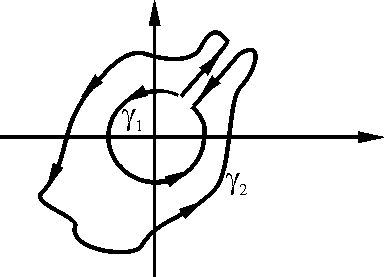
Отметим, что все интегралы по таким контурам совпадают между собой.

И

ллюстрация : 

 .

в). Тогда достаточно вычислить скажем, по окружности . .

г). Легко видеть, что .

Следовательно, , если контур не проходит через точку (0,0) т.к. начальная и конечная точки замкнутого контура совпадают.

2⁰. Найти первообразную, если:

.

Проверка показывает, что условия ; ; выполняются.

Таким образом, задача о нахождении первообразной поставлена корректно. Тогда,

1). и интегрирование по дает: .

Отсюда . Но из условия задачи.

2). Тогда  .

Интегрирование по дает .

Значит: .

Отсюда . Но из условия задачи .

3) Тогда  .

Итог: . Первообразная найдена с точностью до произвольного постоянного слагаемого. Большего и желать не приходится.

§. Элементы теории поверхностей.

1⁰. Пусть в области G Е₃ задана функция F (x, y, z) = 0 и .

Тогда выполняются условия теоремы о неявных функциях и говорят, что в области

G неявно задана поверхность z = z(x,y).

2⁰. Если нам удается разрешить уравнение F (x, y, z) = 0 относительно z, то

получаем поверхность, заданную явно: z = z(x,y).

3

⁰. Если и , то говорят, что в задана гладкая поверхность S, а – называют носителем этой поверхности.

При этом, если и такие, что

,

то поверхность называется поверхностью с самопересечениями, в противном случае – поверхность называется простой.

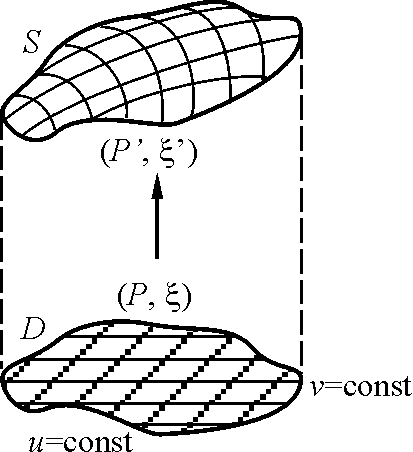
Проведя в области D координатные линии мы, тем самым, индуцируем на поверхности S линии: и , которые называются координатными линиями поверхности.

Векторы: и являются векторами, касательными к координатным

линиям. Из соображений простоты штрих в дальнейшем не будем писать т.е. будем писать:

, .

Рассмотрев в точке векторы и , можно найти вектор перпендикулярный поверхности:

,

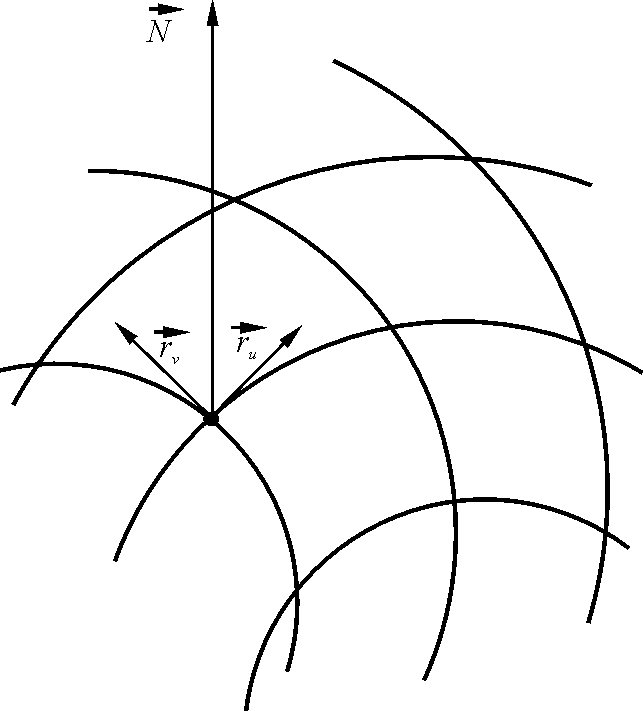
Если ввести обозначения , , , то единичный вектор нормали можно записать так:

.

Можно построить и еще один вектор нормали .

Величины являются направляющими косинусами нормали и поверхности.

В точке (x₀, y₀, z₀) : – уравнение прямой, перпендикулярной к поверхности, а – уравнение плоскости касательной к поверхности .

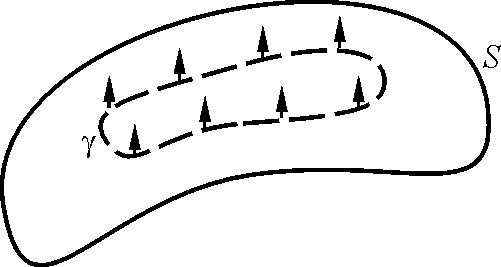
Def. Если на поверхности S существует непрерывный замкнутый контур γ

такой, что при движении по этому контуру (с непрерывным изменением нормали) мы возвращаемся в исходную точку с нормалью имеющей противоположное исходному направлению, то поверхность называется односторонней.

Пример: Лист Мебиуса.

Def. Если для того , чтобы вернуться в исходную точку с направлением

нормали, противоположным исходному, необходимо пересечь край

поверхности, то поверхность называется двухсторонней.

*

). Краем поверхности называется образ границы D в представлении .

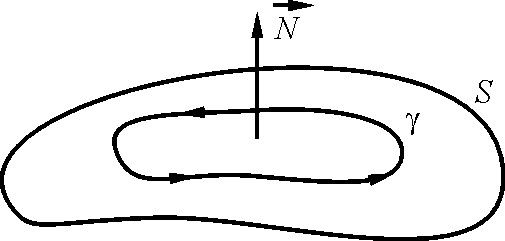
Выбрав на двусторонней поверхности контур γ, зададим на нем ориентацию, указав направление его обхода.

Теперь сориентируем поверхность выбрав на ней направление нормали так, чтобы , если смотреть с конца вектора , движение по контуру γ было против часовой стрелки. Ясно, что такая договоренность означает, что ориентация контура автоматически задает ориентацию (сторону) поверхности и наоборот.