§. Замена переменных в кратных интегралах.
10.
В одинарном интеграле:
.
20. В двойном интеграле:
.
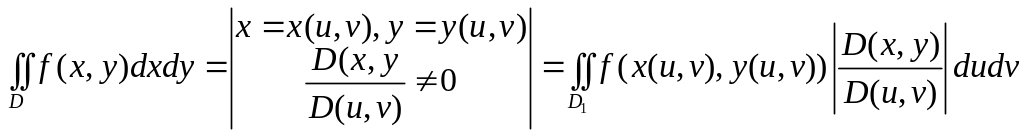30.
В тройном интеграле:
=
=
.
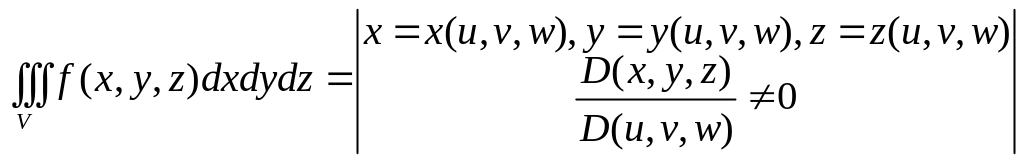40.
В кратном интеграле: если
,
,
и
,
то
.
Примеры:
10.
Вычислить двойной интеграл:
.
Область интегрирования – круг единичного радиуса с центром в начале координат.
a).
В декартовой системе координат:
.
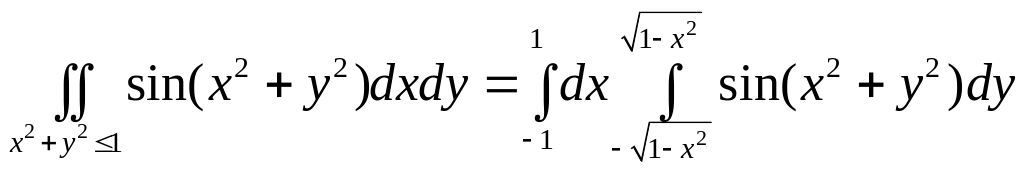Недостатки: пределы интегрирования не красивые и, кроме того, интеграл не выражается через элементарные функции.
б). В полярной системе координат:
.
При
переходе в полярную систему координат
не только получился повторный интеграл
с удобными пределами интегрирования,
но, с учетом того, что внутренний интеграл
не зависит от
получилось даже произведение двух
интегралов Римана.
20.
Вычислить
,
если область D –
замкнутая часть плоскости ограниченная
кривыми: {y = 2x;
y = 4x;
xy = 1; xy
= 3}.
a
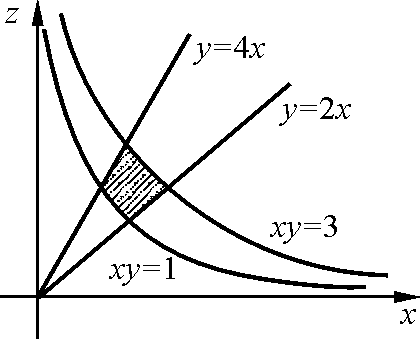
расставлять очень не удобно. Поэтому сделаем по другому.
б).
Сделаем замену переменных: u
= xy, v
=
; 1 ≤ u ≤ 3, 2 ≤
v ≤ 4.
Для
выполнения замены переменных необходимо
найти якобиан
.
Однако находить его неудобно. Поэтому
воспользуемся соотношением: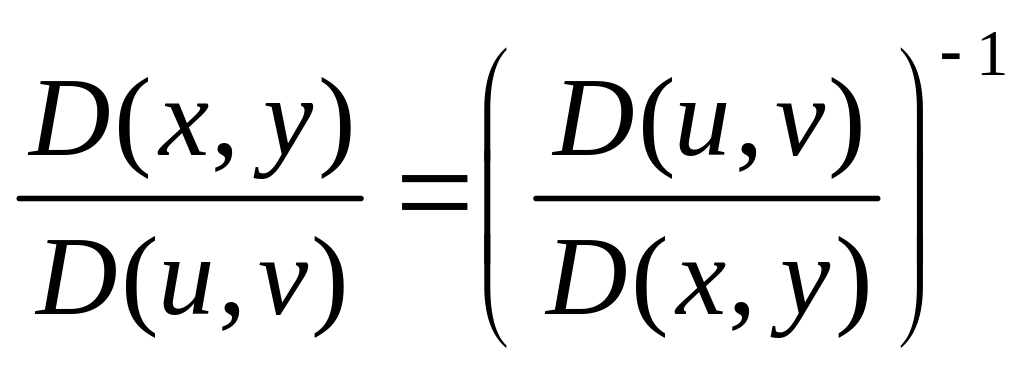
.
Тогда
.
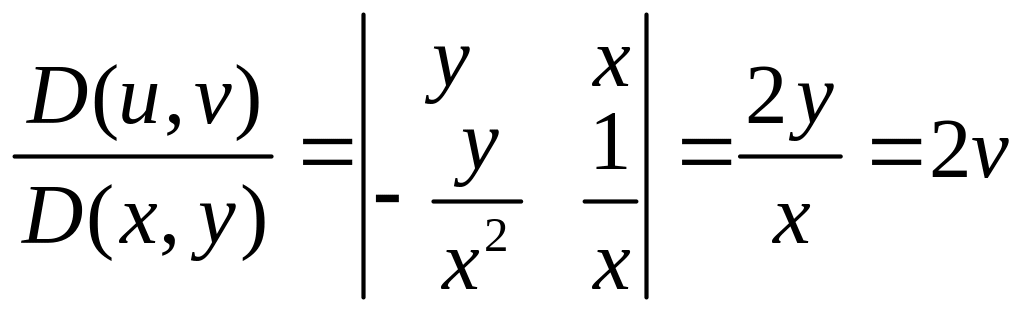Якобиан положителен, следовательно,
ориентация двух систем координат
совпадает. И далее:
=…
30.
Вычислить интеграл
.
I
=
.
Для нахождения полученного двойного
интеграла перейдем в полярную систему
координат.
=
.
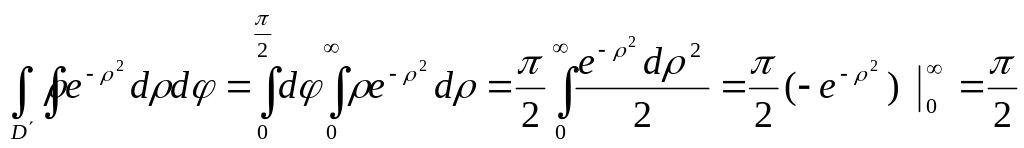Тогда:
.
Пример показывает что не только двойной
интеграл вычисляется с помощью перехода
к повторным, но и наоборот.
§. Криволинейные интегралы 1го рода.
Def
: Если в Е3 задана
вектор-функция
,
и при этом x(t),
y(t),
z(t)
C[a,b],
C1[a,b]
, то говорят, что в Е3 задана
гладкая кривая L.
Пусть на кривой L задана скалярная функция f (x,y,z).
З
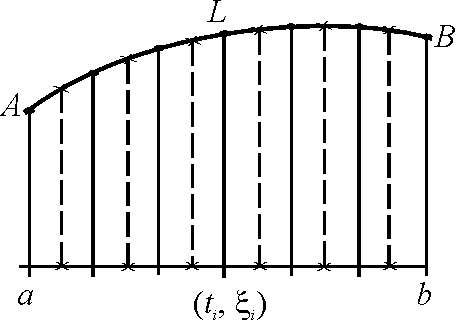
Рассмотрим промежуток [a,b] изменения параметра t , и на [a,b] зададим разбиение P с отмеченными точками ξ, т.е. зададим (P,ξ).
Разбиение (Р,ξ) отрезка [a,b] индуцирует разбиение кривой L с отмеченными точками.
Рассмотрим:
,
где
– длина хорды, соединяющей концы
соответствующего участка кривой. Если
такой предел существует и конечен, то
он называется криволинейным интегралом
1го рода , и обозначается
.
Физический смысл криволинейного интеграла 1го рода – масса кривой L с линейной плотностью масс f (x, y, z).
Для
нахождения элемента длины дуги
будут полезны следующие формулы:
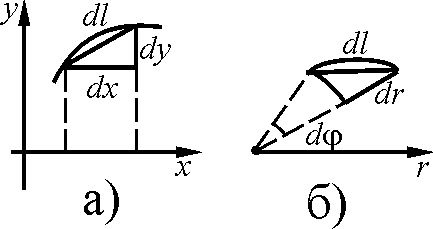
10. Для плоской кривой, заданной в декартовых координатах:
dl
=
(по теореме Пифагора, см. рис. а).
В частных случаях различных способов задания кривой L получаем:
1а.
Если y
= y(x),
то dl
=
;
1б.
Если x
= x(y),
то dl
=
;
1в.
Если x
= x(t),
y = y(t),
то dl =
;
20. Для плоской кривой, заданной в полярных координатах x = ρcosφ, y = ρsinφ:
dl
=
.
Формула эта может быть получена и
непосредственно из криволинейного
треугольника (см. рис. б).
2а.
Если
,
то dl
=
;
2б.
Если
,
то dl
=
;
2в.
Если
,
то dl =
;
30. Для пространственной кривой, заданной в декартовых координатах:
dl
=
.
3а.
Если
,
то dl =
;
40.
Если f (x,
y, z)
= 1 то криволинейный интеграл 1го
рода численно равен длине кривой
и кривая называется спрямляемой.
50.
Криволинейный интеграл
1го рода может быть сведен к
обычному интегралу Римана. Пусть
.
Тогда
.
При этом
.
Формула следует из определения.
40. Криволинейный интеграл 1го рода не зависит от направления интегрирования:
.
Примеры:
10.
Вычислить:
J=
,
где кривая L:
.
Параметрическое
уравнение эллипса:
dl
=
.
Эллипс пробегается против часовой стрелки, хотя это указывать не обязательно.
И тогда:
J
=
=
=
=
.
20.
Найти массу кривой L
: y = ln
x для
,
если ρ = x2 линейная
плотность кривой .
M
=
=
=
=
.
30.
Найти силу притяжения точки А
массы m однородной
полуокружностью радиуса R
с центром в точке А. (
).
,
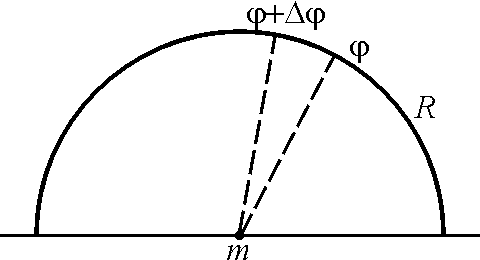
который из соображений симметрии
направлен вверх. Найдем Fy
(т.к. Fx
= 0).
dFy
=
,
где G – гравитационная
постоянная, dl = R
dφ; Следовательно: Fy
=
.