§. Дифференциалы высших порядков.

Определение n дифференциала индуктивное: .

Пусть Тогда:

Найдем второй дифференциал. =

= =

=

= +

+ .

Для второго дифференциала получена формула:

В этой формуле выражение в квадратных скобках в правой части отсутствует, если – независимые переменные, и присутствует если

Это показывает, что форма второго дифференциала не инвариантна относительно замены переменных.

Формула для формального запоминания второго дифференциала для функции n независимых переменных имеет вид: .

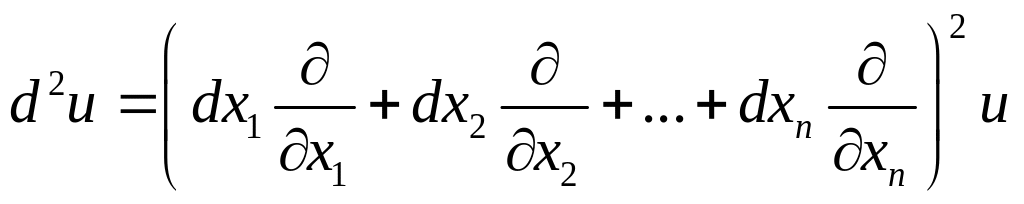а для дифференциала k^-го порядка:

Замечание: Обратим внимание на то, что если функции линейны т.е. имеют вид то второй дифференциал и более дифференциалы более высокого порядка инвариантны по форме.

§. Формула Тейлора.

Напоминание: Для функции одного переменного F(t) ранее была получена формула ее разложения в ряд Тейлора (по формуле Тейлора) в дифференциальной форме:

, где величина .

При этом, – в левой части и dt ­– в правой части совпадают.

В этом виде формула Тейлора справедлива и для функций нескольких переменных.

В дальнейшем, для упрощения письма ограничимся рассмотрением функции двух переменных .

Т. Пусть u = f (x,y) определена и непрерывна в некоторой окрестности точки и имеет в этой окрестности непрерывные производные до (n+1)^-го порядка включительно. Пусть и таковы, что точка принадлежит указанной окрестности.

Тогда: =

= , где . При этом в левой части, совпадают с dx и dy в правой части.

Δ. Соединим точки Р и Р₀ прямолинейным отрезком, принадлежащим упомянутой в формулировке теоремы, окрестности: ; ; .

Подставляя это в , получим .

Тогда: =

= , где .

При этом dt в правой части равенства равно Δt =1–0 =1.

Теперь воспользуемся тем, что при линейной замене переменных высшие дифференциалы инвариантны по форме. (*)

Аналогично для , ,…, и .

Подставляя в формулу (*) получаем требуемое. ▲

§ Экстремумы функций нескольких переменных.

Def: Пусть определена в области D и внутренняя точка области D. Если

то говорят, что в точке функция имеет локальный максимум. Если – локальный минимум, строгий или нет .

Необходимое условие экстремума функции нескольких переменных:

Пусть имеет в точке конечные

У функции зафиксируем Получим Тогда функция как функция одного переменного имеет по

экстремум и, следовательно, . Аналогично

Итак: необходимым условием экстремума дифференцируемой функции

является равенство нулю всех ее частных производных, т.е. точки «подозрительные» на экстремум удовлетворяют системе уравнений:

.

§. Достаточные условия экстремума.

Пусть определена, непрерывна и имеет непрерывные производные первого и второго порядка в некоторой окрестности стационарной точки . Тогда:

Разложим функцию в ряд Тейлора в окрестности стационарной точки.

= .

(При этом . – вычислены в точке , .

Обозначая , получим , где

при , и, следовательно,

.

В силу того, что второе слагаемое в скобках бесконечно мало по сравнению с первым, знак приращения определяется знаком второго дифференциала функции (если он не обращается в нуль). Следовательно от знака второго дифференциала зависит наличие экстремума функции в исследуемой точке.

В алгебре:

Def. Вещественно значная функция векторного аргумента называется квадратичной формой, а квадратная матрица – матрицей квадратичной формы.

Из определения квадратичной формы ясно, что второй дифференциал функции является квадратичной формой , матрица которой состоит из От свойств этой квадратичной формы и зависит имеет ли функция экстремум в рассматриваемой точке или нет.

Def. Квадратичная форма называется положительно определённой, если она принимает положительные значения при всех значениях аргументов, не равных нулю одновременно. , причем .

Def. Квадратичная форма называется отрицательно определённой, если .

Def. Квадратичная форма называется полуопределённой, если

(или ).

Def. Квадратичная форма называется неопределённой, если

и .

Критерий Сильвестра : Для того чтобы квадратичная форма была положительно определённой необходимо и достаточно, чтобы все главные миноры матрицы квадратичной формы были положительны. Для того чтобы квадратичная форма была отрицательно определённой необходимо и достаточно чтобы главные миноры матрицы квадратичной формы чередовались по знаку начиная с минуса:

Если миноры будут ++++… или –+–+… но среди них встречаются нулевые то форма будет полуопределённой. Δ▲.

Пример: Форма имеет матрицу:

А= . Ее миноры:

Все миноры положительны, форма положительно определена . В самом деле, нетрудно проверить, что: .

Т. Если квадратичная форма т.е. второй дифференциал функции,

будет положительно определённой то функция, в испытуемой точке, функция будет иметь минимум; если отрицательно определённой то функция будет иметь максимум.

Если форма полуопределена, то для ответа на вопрос о экстремуме функции требуется привлечение производных более высокого порядка. Во всех остальных случаях – экстремума нет. Δ▲.