§. Формула конечных приращений для функции многих переменных.

=

= =

= .

Δ. Доказательство основано на возможности соединить точки и Р прямолинейным отрезком, принадлежащим области . ▲

§. Производная функции по направлению.

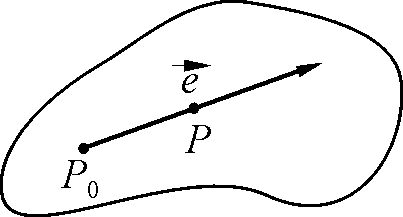
Пусть задана функция трех переменных и в пространстве задано направление . Производной функции по направлению называется .

Запишем параметрическое уравнение прямой проходящей через точки Р и Р₀:

; : .

Тогда: и, значит

.

Если ввести в рассмотрение вектор то получим .

Значит , где  - угол между направлением и направлением .

Следовательно, показывает направление наискорейшего возрастания функции f, а его длина совпадает со скоростью возрастания функции в этом направлении.

§. Инвариантность формы 1го дифференциала при замене переменных.

Пусть , и .

Тогда и

= = =

= =

= = .

То есть: .

Последняя формула выражает свойство инвариантности формы первого дифференциала относительно замены переменных.

§. Производные высших порядков.

Определение производной более высокого порядка, чем первый, можно дать индуктивно. Обозначения для высших производных: .

Пример:

1⁰. Найти частные производные первого и второго порядка функции .

Производные первого порядка: ; ; .

Производные второго порядка:

; ; ;

; ; ;

; ; .

Производные называются вторыми одноименными производными.

Обозначение обозначает, что от функции производная бралась вначале по , а затем по , а при нахождении наоборот, вначале по , а затем по .

Обратим внимание на совпадения соответствующих вторых смешанных производных:

.

Возникает вопрос: случайно ли это совпадение?

2⁰. Рассмотрим функцию, заданную соотношениями:

и .

Функция непрерывна в (0,0) т.к. и, следовательно, .

а)  . б)  .

в) .

Если в положить х = 0, получим,  в (0,0).

г) .

Полагая y = 0, получим,  в (0,0).

Получили, что в точке (0,0). Смешанные производные в точке (0,0) не совпадают.

Итак, вторые смешанные производные не всегда совпадают. А когда?

Т. Пусть определена в открытой области и в этой области, существуют , а также и, наконец, непрерывны в некоторой точке . Тогда: .

Δ. Рассмотрим .

а). Введем вспомогательную функцию . Эта функция дифференцируема: и, следовательно, непрерывна.

Учитывая это, получим:

= = =…

Дважды применим формулу конечных приращений:

…= = .

б) Введем . Тогда аналогично получаем, что

.

Устремим и воспользовавшись непрерывностью в точке получаем: . ▲

В общем случае:

Т⁰. Пусть определена в открытой области евклидового пространства Е_n и имеет в этой области всевозможные частные производные до (n-1)^го порядка включительно и смешанные производные n^го порядка, причем все производные непрерывны в области . Тогда значение любой n^й смешанной производной не зависит от того порядка, в котором производится дифференцирование. Δ▲.