Раздел 9. Дифференцирование функций многих переменных.
§. Частные производные и частные дифференциалы.
Задана функция
переменных
.
Частными приращениями функции называются:
.
Частной производной функции по переменной
называется:
.
Обозначения для частных производных:
Вычисление частной производной по
переменной
производится как обычно и, при этом все
переменные, кроме
,
считаются постоянными.
Примеры.
10.
;
Тогда
20.
;
30.
;
;
.
§. Дифференцируемые функции. Дифференциал.
Т0. Если для функции
существуют частные производные
в некоторой окрестности точки Р0,
и непрерывны в Р0, то
,
где
- бесконечно малые величины.
Δ.
=
=
+
+
+
+
.
Имеем сумму частных приращений. По
формуле конечных приращений для функции
одного переменного получаем:
=
=
.
При
получим:
.
▲.
Def: Функция
называется дифференцируемой в точке
Р0, если возможно представление:
,
(*)
где
– константы, а
при
.
Полагая в (*) (если оно выполнено) все
,
кроме
,
получим:
.
Отсюда запишем: для функции дифференцируемой в Р0:
.
Def: Главная линейная часть
приращения
называется дифференциалом функции
в точке Р0 и обозначается
,
а величины
называются частными дифференциалами.
Если дифференцируема, то
Тогда
Для независимых переменных
и
.
Пример.
.
Пример (контрпример).
Δ. Рассмотрим
;
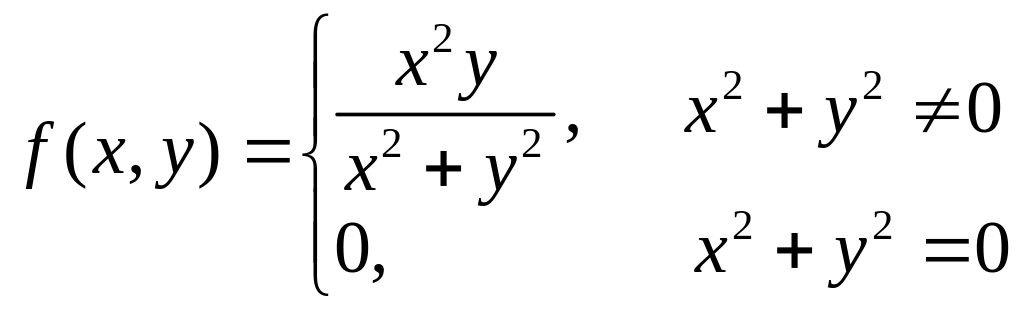Мы уже рассматривали эту функцию и
установили, что в Р0(0, 0) она
непрерывна. Далее:
.
Так как
,
то
и, следовательно, функция
имеет в (0,0) частные производные.
Однако, формула
не имеет места.
В самом деле:
и
не стремится к 0. Связано это с тем, что
в точке Р0 не являются
непрерывными:
и,кроме того,
.
▲
§. Производная сложной функции.
Т0. Если
– функция дифференцируемая в точке Р0
и функции
дифференцируемы в t0 , то функция
дифференцируема в точке t0 и
.
Δ.
=
=
=
.
Это и доказывает дифференцируемость функции и
. ▲
Без труда можно доказать и формулы для дифференцирования сложной функции и в более общем случае:
Пусть
и
.
Тогда для
справедливо:
.
Примеры.
10. Пусть
и
.
Найти
и
.
;
.
20. (контрпример). Пусть
и
.
Найти
.
а)
;
б)
.
Получили результаты, противоречащие один другому. Этот случай показывает, что формула производной сложной функции в этом случае не работает.
NB. Оказывается существование частных производных недостаточно для дифференцируемости (хотя наоборот верно). Дифференцируемость более жесткое требование, чем существование частных производных.