§. Равномерная непрерывность функции на множестве.

Def: Величина называется колебанием функции на множестве М.

Def: Функция называется равномерно непрерывной на множестве М, если

.

Теорема Кантора: Функция непрерывная в ограниченной замкнутой области D равномерно непрерывна на D.

Δ. От противного. Возьмем числовую последовательность , такую что:

и ни одно из этих не годится для равномерной непрерывности.

Тогда , такая что , но . (*)

Получаем последовательность . Из этой последовательности выделим сходящуюся подпоследовательность . Для нее , в силу замкнутости области . Так как , то при .

Значит, в силу непрерывности, , значит , что противоречит (*). ▲

Следствие: Если равномерно непрерывна в ограниченной замкнутой области D, то , таких, что – замкнуты, и выполнено: .

Δ В качестве достаточно взять это число из равномерной непрерывности.

Тогда . ▲

§. Компактные множества в Еn.

Def: Пусть и имеется система множеств = такая, что

. Тогда система множеств = называется покрытием множества М.

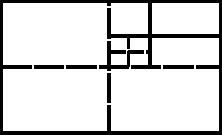
Тº. (Бореля). «Если ограниченное замкнутое множество D покрыто системой = открытых множеств, то из этого покрытия всегда можно выделить конечное.

Δ. От противного. Для наглядности иллюстрации и не ограничивая общности доказательство проведем в двухмерном пространстве. Пусть из существующего бесконечного покрытия нельзя выделить конечное. Проведем процедуру разбиения множества D на прямоугольники с последующим выбором из 4^х прямоугольников одного, который не покрывается конечным покрытием…. Продолжая эту процедуру достаточно долго можно получить сколь угодно маленькие прямоугольники.

На некотором, к^-ом шаге, мы придем к прямоугольнику М_к который содержит ту часть D, которая не покрыта конечным покрытием. Данная последовательность прямоугольников стягивается в точку . Эта точка , т.к. область D – замкнута. Тогда точка входит в одно из множеств покрытия. Так как - открытое множество, то входит в вместе с некоторой своей окрестностью.

В эту окрестность, при достаточно большом k, попадет и прямоугольник М_к, который нельзя покрыть конечным покрытием с одной стороны, а с другой стороны .▲

Def: Множество называется компактом, если из любого его бесконечного покрытия открытыми множествами можно выделить конечное покрытие.

Лемма Бореля показывает, что в Е_n любое ограниченное замкнутое множество является компактом.