Лекция №4 Особые случаи дискретизации: (преобразование сигнала с компактным спектром)
1) Субдискретизация (UnderSampling):
fд может быть в сотни раз меньше, чем по Котельникову в ряде специальных случаев.
Критерий в данном случае: для сигнала с компактным спектром частота дискретизации должна больше, чем в 2 раза, превосходить ширину спектра сигнала.
.
Если проводим дискретизацию → трансляция сигнала из ВЧ области в НЧ.
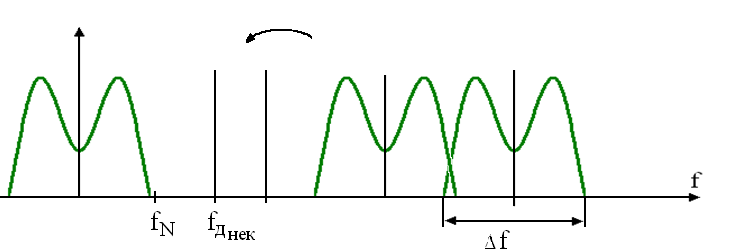
Размножая спектр с точки зрения восстановления сигнала, нет разницы с сигналом из ОПЧ. Всегда есть компонента отраженная в отрицательную область частот.
По
Теореме Котельникова:
Происходит трансляция из верхних зон Найквиста в основную полосу частот. Возьмем частоту дискретизации меньшую, чем Котельникова. Благодаря свойствам трансляции нет смысла использовать критерий Найквиста.
2) Избыточная дискретизация (передискретизация):
Существует избыточная дискретизация Over Sampling (частота fд в несколько сотен раз превышает частоту по теореме Котельникова).
3) Стробоскопическая дискретизация.
Стробоскопические преобразования применяются только для периодических сигналов.
Последовательные точки в разных периодах. Период дискретизации Tд* намного больше Tд, поэтому, обходя теорему Котельникова, резко уменьшаем частоту дискретизации.
→ спектр
дискретного сигнала.
Шум квантования.
Передаточная функция АЦП. Даже идеальный АЦП имеет ошибку.
q/2 - q/2
q – шаг, уровень квантования
Округление квантования- математическая величина, называемая шумом квантования. Погрешность квантования – помеха при восстановлении сигналла.
–
среднее
значение шума квантования (идеальный
случай)
–
среднеквадратичное
значение
– дисперсия, функция распределения (площадь = 1)
S=1
Среднеквадратичное
значение квантования:
Отношение сигнала/шум идеального ацп
Любой даже идеальный АЦП шумит.Вычислим отношение сигнала/шум(динамический диапазон) идеального квантователя. Это выражение используется как при проектировании идеального АЦП, так и в цифровой технике. Выберем в качестве сигнала синусоиду, так как она не меняется при прохождении R-C фильтра. Амплитуда синусоиды укладывается в шкалу АЦП
(среднеквадратичное
значение)
;
n - количество ступенек, q - шаг квантования
,
где n
– разрядность АЦП в битах.
Метод повышения дд. Передискретизация.
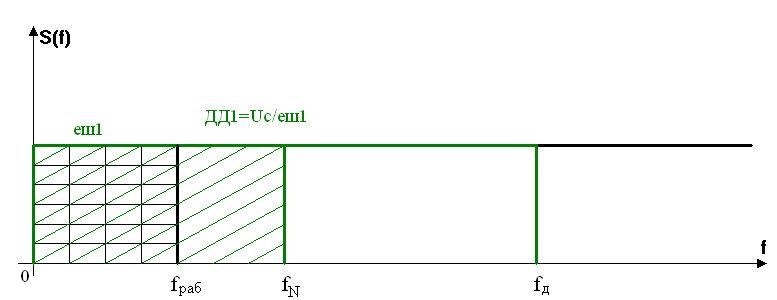
Шум квантования равномерно распределен равномерно от 0 до частоты Найквиста. Площадь под графиком - мощность шума. Остальной шум-результат трансляции спектра.
Если увеличить частоту дискретизации, то мощность шума не изменится, а амплитуда уменьшится. Интересует только шум до рабочей частоты.
Processing gain (выигрыш по обработке, процессорное усиление):
Увеличиваем
в
2 раза → увеличиваем ДД на 3 дБ, т.е.
увеличиваем эффективность разрядности
на 0,5 бит. Для того чтобы увеличить на 1
бит, необходимо увеличить количество
отсчетов
в
4 раза => Используется скользящее
среднее –простейший цифровой фильтр.
Можно использовать усреднение лишних
отсчетов.