Лекция №3 Восстановление аналогового сигнала по выборкам.

Имеем сигнал с симметричным спектром, т. к. исходный сигнал вещественный.

Рассмотрим выборки сигнала:

Какой спектр дискретизованного сигнала?

, где – решётчатая функция стробирования, которую мы должны найти (она вырезаем множество точек).

, где t_Д – шаг дискретизации.

Нужно найти образ s(t) и , затем взять их свёртку:

, где

Тогда спектр дискретного сигнала:

Наблюдаем aliases – сдвинутые копии исходного спектра. Таким образом, спектр дискретизованного сигнала – это размноженный по полосе частот спектр непрерывного сигнала (т.е. он «размножается» с частотой f_д).

Для восстановления требуется полосовой фильтр, который выделит основную полосу частот.

Умножение в частотной области -> свёртка во временной области.

- бесконечный во времени сигнал, если ПФ идеальный.

Нужно вырезать прямоугольное «окно»: окно – идеальный ФНЧ.

– низкочастотная фильтрация (идеальный фильтр). Но т. к. идеальных фильтров в природе не существует, восстановить нельзя.

Теорема Котельникова.

Любую функцию f(t), состоящую из частот от 0 до f_c ( т. е. с ограниченным спектром), можно передавать с любой точностью (в зависимости от типа ФНЧ) с помощью чисел, следующих друг за другом через интервал , если f_д не менее чем в 2 раза превосходит f_c спектра. Т. е. сигнал с ограниченным спектром может быть восстановлен по его дискретным отсчетам, если частота этих отсчетов будет выбрана не меньше, чем удвоенное значение частоты спектра сигнала ( ).

, здесь – выборки, – период дискретизации.

Док-во теоремы Котельникова:

,

где комплексный спектр Фурье:

Спектр ограничен, т.е.: при ω > ω_с.

в интервале частот (-ω_с, ω_с) можно представить рядом Фурье в экспоненциальной форме:

, где

коэффициенты ряда Фурье:

- чётная функция

Окончательно:

(ω_с= ω_max в спектре) #

Не используется, т. к.:

1-Нет сигналов с ограниченным спектром (бесконечное время накопления информации о сигнале).

2-Нет идеальных фильтров нижних частот (физически не реализуем).

Наложение спектров.

Спектр ограничен какой-то частотой → можно размножить → периодическая функция. Но может произойти наложение спектров.

Наложение спектра – подмена одного сигнала другим. Одному и тому же интервалу спектра могут принадлежать разные сигналы.

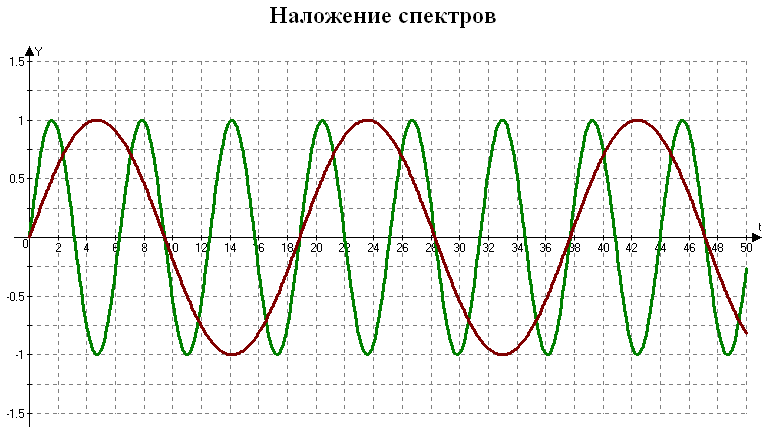
Значения в обеих функциях совпали в моменты дискретизации. Исходя из этого, не можем отличить какой сигнал соответствует данной частоте.

(частота Найквиста)

Первая зона Найквиста – основная полоса частот(ОПЧ). Чётные зоны Найквиста инвертируют сигнал, а нечётные нет.

Чтобы не возникало наложений спектров, нужно выбирать: и .

Восстановление аналогового сигнала по дискретным выборкам

Восстановление сводится к удалению спектральных компонент, всех кроме лежащих в ОПЧ (не обязательно до f_N, в зависимости от картины в ОПЧ) с помощью фильтра низких частот (ФНЧ).

Котельников сформулировал следующую теорему: «Любую функцию f(t), состоящую из частот от 0 до f_c, можно непрерывно передавать с любой точностью при помощи чисел, следующих друг за другом через секунд».