
- •Методичні вказівки
- •4.6. Є такі дані щодо кількості і її ціни поставленої сировини:
- •4.14. Обсяг реалізації побутових послуг населенню України (всього і на душу населення) за 1996-1998 рр. Характеризується такими даними:
- •4.15. Прийом студентів у вищі навчальні заклади України (всього і у тому числі на денне відділення) у 1995/1996 і 1998/1999 навчальних роках складав:
- •4.16. Випуск фахівців вищих навчальних закладів України у 1995/1996 і 1998/1999 н.Р.. Характеризується даними:
- •4.17. Є такі дані щодо випуску акцій у 1998-1999 рр.:
Р о з д і л 4
СЕРЕДНІ ВЕЛИЧИНИ І ПОКАЗНИКИ ВАРІАЦІЇ
Методичні вказівки
Середня величина - це узагальнюючий показник, який характеризує типовий розмір варіюючої ознаки у розрахунку на одиницю однорідної сукупності. У статистичній практиці існує дві форми середніх величин: прості (за первинними, незгрупованими даними) і зважені (за вторинними, згрупованими даними). Розрізняють такі види середніх величин: сумальні і структурні (порядкові). Сумальні середні поділяються на степеневі, логарифмічні, показові, параболічні тощо. У економічних дослідженнях переважне застосування знаходять степеневі середні, серед яких виділяють середню арифметичну, середню гармонічну, середню квадратичну та інші.
У загальному вигляді степенева середня може бути представлена:
- для незгрупованих даних (ряд значень):
![]() (проста);
(проста);
- для згрупованих даних (варіаційний ряд):
 (зважена),
(зважена),
де ![]() -
степенева середня;
-
степенева середня;
![]() -
окремі значення ознаки;
-
окремі значення ознаки;
m - показник степеня;
n – обсяг сукупності;
![]() -
частота.
-
частота.
Базою розрахунку та критерієм правильності вибору форми середньої величини є вхідне співвідношення середньої (змістова формула).
Середня арифметична - найрозповсюджений вид степеневих середніх. Вона застосовується у тих випадках, коли загальний обсяг ознаки, який варіює, для сукупності складається як сума значень ознаки для окремих її одиниць.
Для незгрупованих даних застосовується середня арифметична проста:
![]() .
.
Для згрупованих даних використовується формула середньої арифметичної зваженої:
![]() .
.
Значні спрощення при розрахунку середньої арифметичної зваженої (особливо для варіаційних рядів з рівними інтервалами) надає «метод моментів»:
![]() ,
,
де:
![]() -
довільно вибране значення (віддається
перевага середині центрального інтервалу
або інтервалу, який має найбільшу
частоту);
-
довільно вибране значення (віддається
перевага середині центрального інтервалу
або інтервалу, який має найбільшу
частоту);
![]() -
умовні варіанти в рівних інтервалах
(
-
умовні варіанти в рівних інтервалах
(![]() );
);
![]() -
ширина інтервалу.
-
ширина інтервалу.
Для
сукупності, в якій наведені середні для
окремих її частин (групові або часткові
середні), загальна середня обчислюється
на основі групових середніх (![]() ),
зважених по чисельності відповідних
частин сукупності (
),
зважених по чисельності відповідних
частин сукупності (![]() ):
):
![]() .
.
Середня гармонічна використовується для усереднення варіантів, протилежних індивідуальним значенням.
Для незгрупованих даних використовується середня гармонійна проста:
 ,
,
Для згрупованих даних застосовують середню гармонійну зважену:
 ,
де
,
де![]() .
.
Найбільшого застосування серед описових (структурних середніх) отримали мода і медіана.
Мода
(![]() )
- це величина ознаки (варіанту), яка
найбільш часто зустрічається у сукупності.
У дискретному варіаційному ряду модою
є варіант, який має найбільшу частоту.
У інтервальних варіаційних рядах мода
визначається за формулою:
)
- це величина ознаки (варіанту), яка
найбільш часто зустрічається у сукупності.
У дискретному варіаційному ряду модою
є варіант, який має найбільшу частоту.
У інтервальних варіаційних рядах мода
визначається за формулою:
 ,
,
де:
![]() -
нижня межа модального інтервалу, тобто
інтервалу з найбільшою частотою;
-
нижня межа модального інтервалу, тобто
інтервалу з найбільшою частотою;
![]() -
частота модального інтервалу;
-
частота модального інтервалу;
![]() -
частота передмодального інтервалу;
-
частота передмодального інтервалу;
![]() -
частота післямодального інтервалу;
-
частота післямодального інтервалу;
![]() -
ширина модального інтервалу.
-
ширина модального інтервалу.
Медіана
(![]() )
- це варіанта, яка міститься у середині
варіаційного ряду. У дискретних рядах
порядковий номер медіанного варіанту
визначається як (n+1)/2 (для ряду з непарним
числом n), або як середнє значення двох
середніх варіантів, які мають порядкові
номери n/2 і n/2+1 (для ряду з парним числом
n). У интервальному варіаційному ряду
медіана визначається за формулою:
)
- це варіанта, яка міститься у середині
варіаційного ряду. У дискретних рядах
порядковий номер медіанного варіанту
визначається як (n+1)/2 (для ряду з непарним
числом n), або як середнє значення двох
середніх варіантів, які мають порядкові
номери n/2 і n/2+1 (для ряду з парним числом
n). У интервальному варіаційному ряду
медіана визначається за формулою:
 ,
,
де:
![]() -
нижня межа медіанного інтервалу;
-
нижня межа медіанного інтервалу;
![]() -
сума частот, накопичених до медіанного
інтервалу;
-
сума частот, накопичених до медіанного
інтервалу;
![]() -
сума частот всього варіаційного ряду;
-
сума частот всього варіаційного ряду;
![]() -
ширина медіанного інтервалу;
-
ширина медіанного інтервалу;
![]() -
частота медіанного інтервалу.
-
частота медіанного інтервалу.
При вивченні структури варіаційного ряду, окрім медіани, використовуються також квартилі, що ділять ряд за сумою частот на 4 рівні частини, і децилі - на 10 рівних частин. Квартилів налічується 3, а децилів - 9. Розрахунок цих показників у інтервальному варіаційному ряду аналогічний розрахунку медіани. Формула для квартилів у інтервальних варіаційних рядів має вид:
 ,
,
де:
![]() -
номер квартиля;
-
номер квартиля;
![]() -
нижні межі відповідних квартильних
інтервалів;
-
нижні межі відповідних квартильних
інтервалів;
- сума частот ряду;
![]() -
сума частот, накопичених до відповідних
квартильних інтервалів;
-
сума частот, накопичених до відповідних
квартильних інтервалів;
![]() -
частоти відповідних квартильних
інтервалів;
-
частоти відповідних квартильних
інтервалів;
![]() -
величини відповідних квартильних
інтервалів.
-
величини відповідних квартильних
інтервалів.
При вивченні статистичних сукупностей поряд з середніми величинами велике практичне значення має вивчення варіації ознак. Для виміру і оцінки варіації використовуються абсолютні і відносні показники варіації: розмах варіації, середнє лінійне відхилення, дисперсія, середнє квадратичне відхилення, коефіцієнт варіації та інші.
Розмах
варіації
(![]() )
характеризує діапазон варіації і
обчислюється як різниця між максимальним
(
)
характеризує діапазон варіації і
обчислюється як різниця між максимальним
(![]() )
та мінімальним (
)
та мінімальним (![]() )
значеннями ознаки:
)
значеннями ознаки:
![]() .
.
Середнє лінійне відхилення (Л) являє собою середню арифметичну з абсолютних значень відхилень окремих варіантів від їхньої середньої арифметичної:
![]() (для
ряду значень, тобто для незгрупованих
даних),
(для
ряду значень, тобто для незгрупованих
даних),
![]() (для
варіаційного ряду, тобто для згрупованих
даних)
(для
варіаційного ряду, тобто для згрупованих
даних)
Дисперсія
(![]() )
являє собою середній квадрат відхилення
варіантів від їх середньої арифметичної:
)
являє собою середній квадрат відхилення
варіантів від їх середньої арифметичної:
![]() (для
ряду значень)
(для
ряду значень)
![]() (для
варіаційного ряду)
(для
варіаційного ряду)
Для обчислення дисперсії на практиці використовуються спрощені способи розрахунку:
![]() ;
; ![]() ,
,
де:
![]() -
середня арифметична квадратів умовних
варіант:
-
середня арифметична квадратів умовних
варіант:
 -
квадрат середньої арифметичної умовних
варіант:
-
квадрат середньої арифметичної умовних
варіант:
![]() -
середня арифметична квадратів варіантів;
-
середня арифметична квадратів варіантів;
![]() -
квадрат середньої арифметичної.
-
квадрат середньої арифметичної.
Середнє
квадратичне відхилення
(![]() )
характеризує міру абсолютного
коливання ознаки відносно середньої
величини і розраховується як корінь
квадратний із дисперсії:
)
характеризує міру абсолютного
коливання ознаки відносно середньої
величини і розраховується як корінь
квадратний із дисперсії:
![]() (для
ряду значень)
(для
ряду значень)
 (для
варіаційного ряду)
(для
варіаційного ряду)
Коефіцієнт
варіації
(![]() )
характеризує відносне коливання значень
ознаки відносно середньої і являє собою
виражене у відсотках (або у вигляді
частки) відношення середнього лінійного
або середнього квадратичного відхилення
до середньої величини:
)
характеризує відносне коливання значень
ознаки відносно середньої і являє собою
виражене у відсотках (або у вигляді
частки) відношення середнього лінійного
або середнього квадратичного відхилення
до середньої величини:
![]() ;
; ![]() .
.
Якщо статистична сукупність розбита на групи за певною ознакою, то для такої сукупності можуть бути розраховані такі дисперсії: загальна, групові (внутрішньогрупові), середня від групових, міжгрупова.
Загальна дисперсія ( ) вимірює варіацію ознаки всієї сукупності під впливом усіх чинників, які зумовили цю варіацію, і обчислюється за однією з формул, наведених вище.
Внутрішньогрупові дисперсії показують значення варіацій в кожній групі, зумовлені усіма чинниками, окрім чинника, покладеного в основу групування:

Середня з групових дисперсій відображає варіацію, зумовлену всіма чинниками, окрім чинника, покладеного в основу групування, але у середньому по сукупності:
![]() .
.
Міжгрупова дисперсія характеризує варіацію групових середніх, зумовлену впливом ознак, за якими проведено групування:
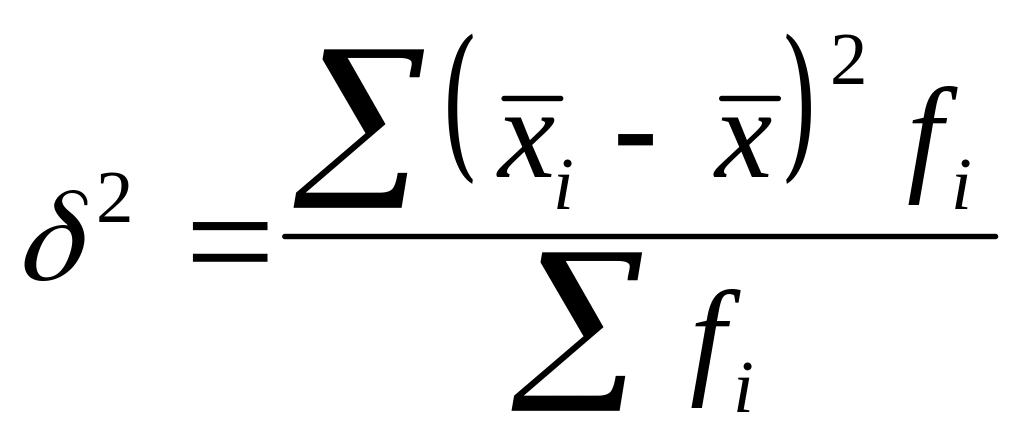
Загальна дисперсія дорівнює сумі середньої з групових дисперсій та міжгруповій дисперсії. Це називається правилом розкладання варіації:
![]() .
.
Відношення міжгрупової дисперсії до загальної показує, яка частина загальної варіації ознаки зумовлена варіацією ознаки, за якою проведено групування, і носить назву емпіричного коефіцієнта детермінації:
![]() .
.
Для оцінки щільності зв'язку між ознакою групування та результативною ознакою обчислюється емпіричне кореляційне відношення:
![]() .
.
З а д а ч і
Прибуток п'яти сімей характеризуються такими даними:
Показники |
Сім'ї |
||||
1 |
2 |
3 |
4 |
5 |
|
Прибуток, грн. |
450 |
800 |
480 |
500 |
900 |
Число членів сім'ї, осіб |
3 |
4 |
3 |
2 |
4 |
Визначте:
Середній прибуток на одну сім’ю.
Середній прибуток на одного члена сім'ї (для кожної сім’ї окремо і для всіх сімей загалом).
Результати проаналізуйте.
4.2. Є такі дані щодо результатів іспиту з мікроекономіки для студентів двох груп:
Порядковий номер студента |
Оцінки |
|
1 група |
2 група |
|
1 |
3 |
4 |
2 |
5 |
3 |
3 |
2 |
5 |
4 |
3 |
4 |
5 |
4 |
5 |
6 |
5 |
5 |
7 |
4 |
3 |
8 |
3 |
5 |
9 |
5 |
4 |
10 |
5 |
5 |
1. По кожній групі cкладіть варіаційний ряд, який характеризує розподіл студентів за балом.
2. Визначте середній бал студентів кожної групи: а) способом простої (незваженої) середньої; б) способом зваженої середньої.
Порівняйте результати. Зробіть висновки.
4.3. Є такі дані щодо обсягу і курсу продажу акцій на аукціонах:
Аукціони |
Кількість проданих акцій
|
Курс продажу 1 акції, грн. |
1 |
200 |
105 |
2 |
300 |
120 |
3 |
1000 |
150 |
Визначте:
1. Середню кількість проданих акцій.
2. Середній курс продажу 1 акції.
Зробіть висновки.
4.4. На протязі 7-годинного робочого дня бригада токарів була зайнята виготовленням однакових деталей. Витрати часу першого токаря на виготовлення однієї деталі становили 15 хвилин, другого - 13, третього - 12, четвертого - 14 і п'ятого - 16 хвилин.
Визначте середній час для виготовлення однієї деталі.
4.5. Є такі дані по двом заводам, які виробляють однорідну продукцію:
|
1999 р. |
2000 р. |
||
Номер заводу |
Витрати часу на одиницю продукції, годин |
Виготовлено продукції, штук |
Витрати часу на одиницю продукції, годин |
Виготовлено продукції, штук |
1 |
2.0 |
200 |
1.9 |
570 |
2 |
3.0 |
250 |
3.0 |
840 |
Обчисліть середні витрати часу на виготовлення одиниці продукції по двом заводам у 1999 і 2000 рр. Вкажіть, який вид середньої треба використати для обчислення цих показників.
Визначте характеристику динаміки середніх витрат часу на виготовлення одиниці продукції для кожного заводу і по двом заводам разом.
Зробіть висновки.
