
- •Часть II
- •Содержание
- •0. Лазерный нагрев материалов 7
- •1. Лазерное разрушение поглощающих материалов 92
- •0. Современные представления об оптическом пробое прозрачных сред 136
- •Глава 0. Воздействие сверхкоротких лазерных импульсов на материалы 150
- •Введение
- •0. Лазерный нагрев материалов
- •0.1. Общая характеристика нагревания лазерным излучением
- •0.0.0. Тепловые эффекты в конденсированных средах
- •0.0.1. Основные особенности температурной кинетики при лазерном воздействии на металлы
- •0.0.2. Теплопроводностные механизмы отвода тепла. Уравнение теплопроводности, начальное и граничные условия
- •0.1. Термические эффекты, сопровождающие лазерный нагрев
- •0.1.0. Термомеханические эффекты
- •0.1.1. Фазовые переходы в твердом состоянии (лазерное упрочнение)
- •0.1.2. Эмиссионные процессы
- •0.1.3. Основные особенности лазерной активации процессов аррениусовского типа. Лазерное окисление
- •0.1.4. Диффузионно-химические явления
- •0.1.5. Экзотермические эффекты при импульсном лазерном воздействии на металлы
- •0.2. Линейные режимы лазерного нагрева
- •0.2.0. Понятие температуры электронной и решеточной подсистем
- •0.2.1. Нагрев полупространства экспоненциально спадающим с глубиной тепловым источником
- •0.2.2. Нагрев металла импульсным излучением постоянной мощности
- •0.2.3. Нагрев материала лазерным пучком с гауссовым профилем
- •0.2.4. Нагрев материала постоянным лазерным излучением, луч сфокусирован в пятно круглого сечения
- •0.2.5. Влияние временной зависимости интенсивности лазерного излучения
- •0.2.6. Лазерный нагрев тонких слоев и пленок
- •0.2.7. Нагрев материалов в интерференционном лазерном поле
- •0.2.8. Особенности нагрева материала движущимся световым пятном.
- •0.3. Нелинейные режимы лазерного нагрева
- •0.3.0. Нагрев с учетом температурной зависимости поглощательной способности
- •0.3.1. Изменение поглощательной способности окисляющихся материалов при лазерном нагревании. Тепловая неустойчивость
- •0.3.2. Интерференционные явления в окисном слое
- •0.4. Лазерное плавление поверхности
- •0.4.0. Вакансионная модель плавления
- •Контрольные вопросы к разделу 1
- •1. Лазерное разрушение поглощающих материалов
- •1.0. Общая характеристика механизмов лазерного разрушения
- •1.0. Механическое низкотемпературное разрушение хрупких материалов
- •1.0.0. Разрушение упругими напряжениями
- •1.0.1. Разрушение остаточными напряжениями
- •1.1. Химические механизмы разрушения
- •1.2. Высокотемпературные механизмы с участием испарения
- •1.3. Поляритонный механизм формирования лазерно-индуцированного поверхностного рельефа
- •1.4. Лазерное испарение
- •1.4.0. Кинетика испарения плоской поверхности
- •1.4.0.0. Испарение в вакуум и среду с противодавлением
- •1.4.0.1. Температурная граница перехода от нагрева к испарению
- •1.4.1. Теплофизика перехода от нагрева к испарению
- •1.4.2. Одномерная задача о лазерном нагреве с испарением
- •1.4.2.0. Установление стационарного режима. Определение квазистационарных параметров
- •1.4.2.1. Зависимость температуры и скорости лазерного разрушения от плотности светового потока.
- •1.4.3. Вытеснение расплава избыточным давлением паров
- •1.5. Свойства лазерного пара и плазмы, их влияние на процесс разрушения
- •Контрольные вопросы к разделу 2
- •0. Современные представления об оптическом пробое прозрачных сред
- •0.0. Физические представления об оптическом пробое идеальных диэлектриков
- •0.0.0. Оптический пробой газов
- •0.0.1. Оптический пробой идеально чистых твердых тел
- •0.1. Тепловой механизм оптического пробоя реальных сред
- •0.1.0. Основные экспериментальные закономерности и особенности оптического пробоя и разрушения оптически неоднородных сред
- •0.1.1. Тепловая неустойчивость
- •0.1.2. Статистическая концепция оптического пробоя
- •0.1.3. Размерная зависимость порога пробоя
- •Контрольные вопросы к разделу 3
- •Глава 0. Воздействие сверхкоротких лазерных импульсов на материалы
- •0.0. Двухтемпературная модель при сверхкоротком воздействии
- •0.1. Особенности экспериментального изучения воздействия фемтосекундных лазерных импульсов на материалы
- •0.2. Особенности разлета вещества при фемтосекундном лазерном воздействии
- •0.3. Плавление при воздействии сверхкоротких лазерных импульсов
- •0.3.0. Термическое плавление с высокими скоростями
- •0.3.1. Нетермическое плавление
- •0.4. Фотофизическая абляция
- •0.5. Уплотнение электронного газа и кулоновский взрыв в поверхностном слое проводника
- •0.6. Формирование лазерно-индуцированного поверхностного рельефа при воздействии сверхкоротких лазерных импульсов
- •0.6.0. Механизм образования поверхностных периодических структур при воздействии сверхкоротких импульсов
- •0.6.1. Резонансная дифракция на плоской поверхности с периодической модуляцией оптических свойств
- •0.6.2. Формирование периодического профиля поля температур
- •0.6.3. Эволюция периодических поверхностных структур в расплавленном поверхностном слое
- •0.7. Силовое действие сверхкоротких импульсов на прозрачные диэлектрики
- •Контрольные вопросы к разделу 4
- •Список рекомендуемой литературы
- •Кафедра лазерных технологий и экологического приборостроения
- •История кафедры лт и эп делится на
- •4 Разных периода:
- •1) Лазерное формирование многофункциональных зондов (мз) для зондовой микроскопии с целью создания универсальных зондовых микроскопов.
- •3) Наноструктурирование тонких металлических и полупроводниковых слоев.
- •4) Управление микрогеометрией, наношероховатостью и физико–химичекими свойствами поверхности материалов
- •2. Лаборатория лазерной очистки и реставрации произведений культуры и искусства (пкин) организована совместно с фирмой ооо «Мобильные лазерные системы».
- •Взаимодействие лазерного излучения с веществом (силовая оптика).
0.5. Уплотнение электронного газа и кулоновский взрыв в поверхностном слое проводника
Как
уже было отмечено, обычно эксперименты
проводят при плотностях энергии
нагревающего излучения – не выше 10
мДж/см2 (пиковая температура
электронного газа
порядка 104 К значительно ниже
характерной температуры Ферми
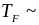 105
К). В случае более высоких значений
105
К). В случае более высоких значений
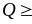 0,1
Дж/см2 (пиковые
0,1
Дж/см2 (пиковые
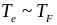 )
получены экспериментальные результаты,
свидетельствующие о возможности
реализации другого типа электрон-решеточного
взаимодействия при субпикосекундном
разупорядочивании кристаллической
решетки металлов ("электронное
плавление").
)
получены экспериментальные результаты,
свидетельствующие о возможности
реализации другого типа электрон-решеточного
взаимодействия при субпикосекундном
разупорядочивании кристаллической
решетки металлов ("электронное
плавление").
Приведем
результаты экспериментов, проведенных
по методике, использованной для
обнаружения нетермического плавления,
но при плотностях энергии значительно
выше порога нетермического плавления
( 0,25
Дж/см2).
0,25
Дж/см2).
В
качестве мишеней использовались пленки
и
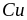 (толщиной 30 40 нм)
на стекле, а также оптически "толстые"
металлические пленки расплава
(толщиной 30 40 нм)
на стекле, а также оптически "толстые"
металлические пленки расплава
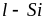 или
или
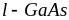 толщиной до 20 нм, получаемые на поверхности
объемных нелегированных образцов этих
материалов (
)
под действием и в течение того же импульса
накачки с эффективной плотностью энергии
толщиной до 20 нм, получаемые на поверхности
объемных нелегированных образцов этих
материалов (
)
под действием и в течение того же импульса
накачки с эффективной плотностью энергии
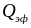 на образце выше порога нетермического
плавления (
0,25
Дж/см2 и 0,15 Дж/см2, соответственно).
на образце выше порога нетермического
плавления (
0,25
Дж/см2 и 0,15 Дж/см2, соответственно).
Для
всех указанных образцов экспериментально
исследованы зависимости коэффициента
самоотражения
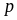 -поляризованного
излучения накачки (для
-поляризованного
излучения накачки (для
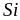 и
также
-поляризованного)
от его энергии. Полученные зависимости
коэффициента самоотражения излучения
накачки
и
также
-поляризованного)
от его энергии. Полученные зависимости
коэффициента самоотражения излучения
накачки
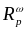 (для
и
-
и
(для
и
-
и
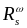 )
от энергии импульса накачки были
обработаны по методике, использованной
при обработке данных в эксперименте по
нетермическому плавлению. Напомним,
что в основе упомянутой процедуры лежит
предположение о зависимости величин
и
от
вложенной в течение лазерного импульса
мгновенной эффективной плотности
)
от энергии импульса накачки были
обработаны по методике, использованной
при обработке данных в эксперименте по
нетермическому плавлению. Напомним,
что в основе упомянутой процедуры лежит
предположение о зависимости величин
и
от
вложенной в течение лазерного импульса
мгновенной эффективной плотности
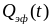 ,
а не интенсивности
,
а не интенсивности
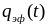 ,
что достаточно справедливо при воздействии
на металлы сверхкоротких импульсов с
умеренными значениями
,
что достаточно справедливо при воздействии
на металлы сверхкоротких импульсов с
умеренными значениями
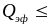 10
Дж/см2. Результирующие зависимости
10
Дж/см2. Результирующие зависимости
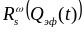 и
и
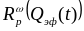 представлены на рис. 0.19 (вертикальная
пунктирная линия показывает положение
порога плавления
и
в течение импульса накачки, стрелка -
начало аномалии оптических свойств
(плато
и
)
для всех образцов).
представлены на рис. 0.19 (вертикальная
пунктирная линия показывает положение
порога плавления
и
в течение импульса накачки, стрелка -
начало аномалии оптических свойств
(плато
и
)
для всех образцов).
Приведенные
зависимости
свидетельствуют, что при воздействии
на все типы металлических пленок
излучения с характерной
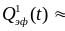 0,2
Дж/см2 наблюдается плато величины
в диапазоне значений 0,5
0,6. Аналогичный эффект ранее наблюдался
для лазерно-индуцированного расплава
пленок
и
0,2
Дж/см2 наблюдается плато величины
в диапазоне значений 0,5
0,6. Аналогичный эффект ранее наблюдался
для лазерно-индуцированного расплава
пленок
и
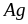 при близких значениях
и объяснялся в рамках двухтемпературной
модели значительным уменьшением
характерного времени электрон-электронного
рассеяния
при близких значениях
и объяснялся в рамках двухтемпературной
модели значительным уменьшением
характерного времени электрон-электронного
рассеяния
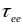 до 10-16 с
при нагреве электронной подсистемы до
105 К. Вместе с тем, отмечаемая на
рис. 0.19 особенность зависимостей
до 10-16 с
при нагреве электронной подсистемы до
105 К. Вместе с тем, отмечаемая на
рис. 0.19 особенность зависимостей
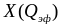 вблизи
вблизи
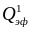 резкое уменьшение
глубины кратера до ширины скин-слоя
указывает на более сложный характер
процессов, происходящих в скин-слое
проводника при таких высоких степенях
нагрева.
резкое уменьшение
глубины кратера до ширины скин-слоя
указывает на более сложный характер
процессов, происходящих в скин-слое
проводника при таких высоких степенях
нагрева.
С
использованием зависимостей
и
для проводящих пленок
и
были исследованы их оптические
характеристики
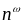 и
и
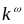 вблизи
(рис. 0.20).
вблизи
(рис. 0.20).
Для
указанных образцов выше порога плавления
отмечается непрерывный рост величины
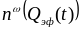 при постоянстве
,
что указывает на неоднородность
оптических свойств вещества в пределах
скин-слоя. В то же время, превышение
над
при
при постоянстве
,
что указывает на неоднородность
оптических свойств вещества в пределах
скин-слоя. В то же время, превышение
над
при
 означает, что в пределах скин-слоя
появляется диэлектрическая фаза с
положительной величиной действительной
части диэлектрической проницаемости.
С целью выяснения природы наблюдаемых
аномалий с использованием эффективных
значений
и
были получены соответствующие зависимости
эффективных значений плазменной частоты
означает, что в пределах скин-слоя
появляется диэлектрическая фаза с
положительной величиной действительной
части диэлектрической проницаемости.
С целью выяснения природы наблюдаемых
аномалий с использованием эффективных
значений
и
были получены соответствующие зависимости
эффективных значений плазменной частоты
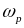 и
от
(рис. 0.20, вертикальная пунктирная линия
показывает положение порога плавления
и
в течение импульса накачки, стрелка -
начало аномалии оптических свойств для
указанных образцов), показывающие, что
при
происходит резкий рост
и падение
.
и
от
(рис. 0.20, вертикальная пунктирная линия
показывает положение порога плавления
и
в течение импульса накачки, стрелка -
начало аномалии оптических свойств для
указанных образцов), показывающие, что
при
происходит резкий рост
и падение
.
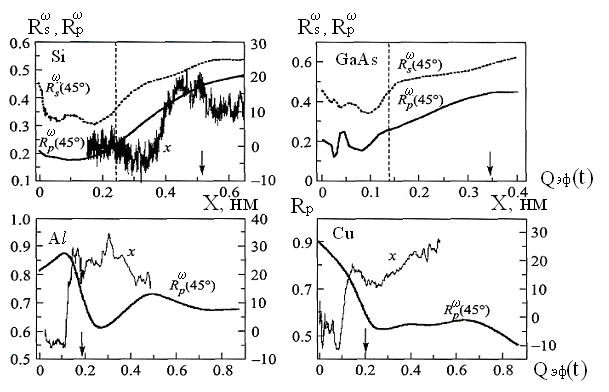
Рис.
0.19. Зависимости коэффициента самоотражения
и
от мгновенной эффективной (поглощенной)
плотности энергии
накачки для образцов
,
,
и
и глубины (профиля) кратера
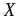 от интегральной
для образцов
,
и
от интегральной
для образцов
,
и
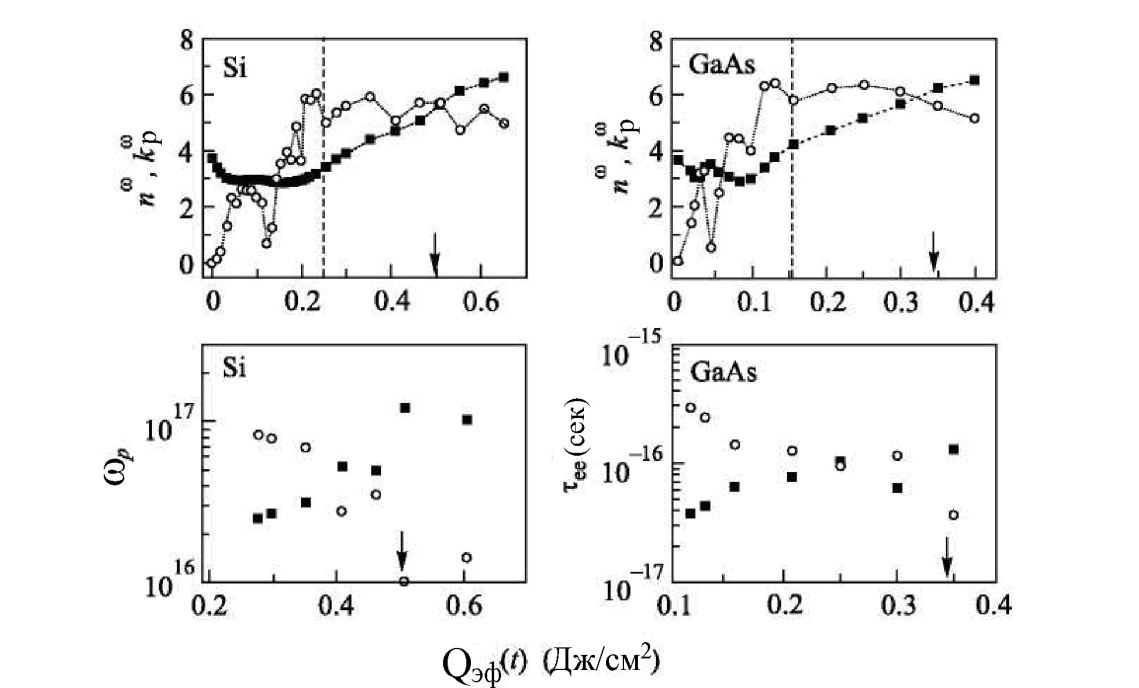
Рис.
0.20. Зависимости оптических констант
и
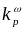 ,
а также
и
от
для образцов
и
(аналогичные оси для обоих образцов
совмещены)
,
а также
и
от
для образцов
и
(аналогичные оси для обоих образцов
совмещены)
Падение
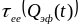 при
можно объяснить в рамках теории
ферми-жидкости ростом
и
(рис. 0.20), причем последняя, как и
соответствующие постоянные
электрон-электронного рассеяния
при
можно объяснить в рамках теории
ферми-жидкости ростом
и
(рис. 0.20), причем последняя, как и
соответствующие постоянные
электрон-электронного рассеяния
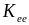 (2,5 и 1,5 фс-1·эВ-2
для
(2,5 и 1,5 фс-1·эВ-2
для
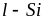 и
и
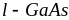 ,
соответственно), рассчитывались согласно
выражениям
,
соответственно), рассчитывались согласно
выражениям
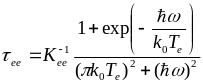 (0.18)
(0.18)
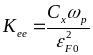 (0.19)
(0.19)
с
использованием зависимостей
и
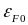 от
(рис. 0.20, 0.21) и подгоночного параметра
от
(рис. 0.20, 0.21) и подгоночного параметра
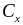 ,
оцениваемого при
,
оцениваемого при
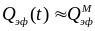 (то есть при
(то есть при
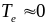 ).
).
Поскольку
для
и
измеренная оптическая масса электрона
равняется единице, то наблюдаемый
значительный монотонный рост
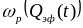 можно связать с соответствующим ростом
эффективной плотности электронов
можно связать с соответствующим ростом
эффективной плотности электронов
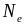 в скин-слое, а, следовательно, и эффективной
энергии Ферми
(рис. 0.21).
в скин-слое, а, следовательно, и эффективной
энергии Ферми
(рис. 0.21).
Зависимости
,
и
от
(рис. 0.21, стрелка показывает порог
появления аномалии
,
и
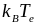 в течение импульса накачки) показывают,
что, несмотря на значительный рост
в течение импульса накачки, вырождение
электронного газа в скин-слое металлических
пленок
и
сохраняется вследствие роста его
эффективной плотности
,
который, по-видимому, имеет термоэлектрическую
природу. Так, с ростом
в течение импульса накачки) показывают,
что, несмотря на значительный рост
в течение импульса накачки, вырождение
электронного газа в скин-слое металлических
пленок
и
сохраняется вследствие роста его
эффективной плотности
,
который, по-видимому, имеет термоэлектрическую
природу. Так, с ростом
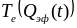 в скин-слое пленок
и
возникают градиенты температуры
в скин-слое пленок
и
возникают градиенты температуры
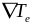 и давления электронного газа
и давления электронного газа
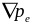 ,
где
,
где
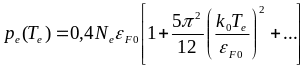 .
(0.20)
.
(0.20)
В
скин-слое на длине градиента
происходит дрейфовый перенос электронного
газа, причем по мере смещения распределения
от поверхности образца происходит
смещение в глубь скин-слоя "эффективной
поверхности" последнего, то есть
поверхности максимального энерговыделения,
и обострение
.
Это приводит к еще более быстрому (по
сравнению с лежащими глубже слоями
движущегося распределения
)
смещению в глубь скин-слоя его "эффективной
поверхности", обострению
и дальнейшему уменьшению реальной
ширины скин-слоя (то есть сжатию
электронного газа и соответствующему
росту локального коэффициента поглощения).
Очевидно, что задний фронт распределения
,
смещающегося в объем под действием
,
распространяется быстрее его переднего
фронта, постепенно порождая нестационарную
"ударную" волну
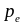 сжимающую электронный газ у переднего
фронта. Экспоненциальный характер
нарастания зависимостей
,
и
от мгновенной
(рис. 0.21), представляющих собой набор
мгновенных значений данных параметров
в течение лазерного импульса, подтверждает
предложенную выше нестационарную
картину явления.
сжимающую электронный газ у переднего
фронта. Экспоненциальный характер
нарастания зависимостей
,
и
от мгновенной
(рис. 0.21), представляющих собой набор
мгновенных значений данных параметров
в течение лазерного импульса, подтверждает
предложенную выше нестационарную
картину явления.
Вместе
с тем, очевидно, что при распространении
такой волны с ростом
увеличение степени экранирования ионов
электронным газом приведет к насыщению
поглощения на "эффективной поверхности"
скин-слоя при величине
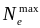 и дальнейшая эволюция "ударной"
волны при наличии лазерного излучения
будет происходить за счет увеличения
пространственной ширины скачка уплотнения
с амплитудой
и, по-видимому, образования универсального
"плазменного зеркала", наблюдавшегося
для широкого круга материалов при
1015
Вт/см2. Заметим, что для пленки
достигается двадцатикратное уплотнение
электронного газа без каких-либо
признаков насыщения зависимости
и дальнейшая эволюция "ударной"
волны при наличии лазерного излучения
будет происходить за счет увеличения
пространственной ширины скачка уплотнения
с амплитудой
и, по-видимому, образования универсального
"плазменного зеркала", наблюдавшегося
для широкого круга материалов при
1015
Вт/см2. Заметим, что для пленки
достигается двадцатикратное уплотнение
электронного газа без каких-либо
признаков насыщения зависимости
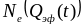 (рис. 0.21).
(рис. 0.21).
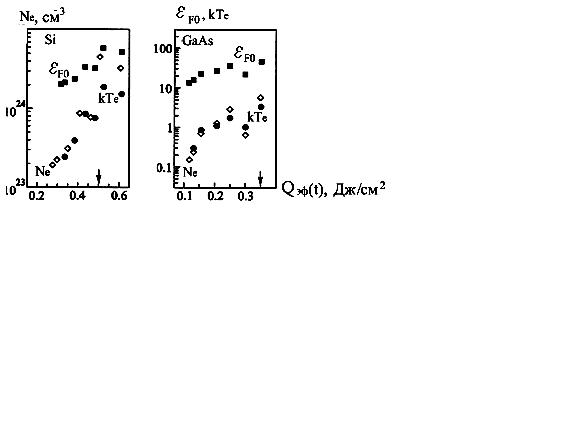
Рис. 0.21. Зависимости , и от для образцов и
Очевидно,
что по мере пробега "ударной" волны
в пределах скин-слоя может образоваться
двойной электрический слой из
"поверхностного" слоя положительно
заряженных ионов и "подповерхностного"
слоя сверхплотного и "холодного"
вырожденного электронного газа. Толщина
слоя ионов с плотностью
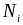 и зарядовым состоянием
и зарядовым состоянием
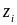 ,
а также электронного слоя оценивается
из условия электронейтральности
,
а также электронного слоя оценивается
из условия электронейтральности
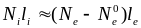 ,
где
,
где
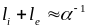 и
и
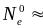 21023
см-3 – равновесная плотность
электронов для пленок
и
.
21023
см-3 – равновесная плотность
электронов для пленок
и
.
Для
средней объемной плотности энергии в
скин-слое при
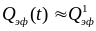 около 10 эВ/атом, близкой к величине
первого потенциала ионизации атомов
,
около 10 эВ/атом, близкой к величине
первого потенциала ионизации атомов
,
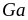 ,
,
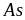 ,
и
(8,2, 6,0, 9,8, 6,0 и 7,7 эВ), имеем
,
и
(8,2, 6,0, 9,8, 6,0 и 7,7 эВ), имеем
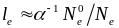 и
и
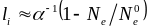 ,
где
,
где
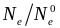 фактор уплотнения
слоя электронного газа.
фактор уплотнения
слоя электронного газа.
При
достигнутых уплотнениях электронного
газа около 10 – 20 величина
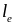 составляет ~ 1 нм и уменьшается с ростом
,
тогда как
составляет ~ 1 нм и уменьшается с ростом
,
тогда как
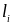 возрастает, соответственно, до
возрастает, соответственно, до
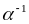 .
Для
.
Для
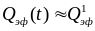 непосредственно после окончания импульса
накачки напряженность внутреннего
электрического поля двойного электрического
слоя составляет согласно уравнению
Пуассона
непосредственно после окончания импульса
накачки напряженность внутреннего
электрического поля двойного электрического
слоя составляет согласно уравнению
Пуассона
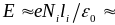 1013
В/м (разность потенциалов
1013
В/м (разность потенциалов
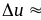 105
В), что качественно согласуется с
экспериментальными данными.
105
В), что качественно согласуется с
экспериментальными данными.
Для
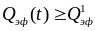 в течение первой пикосекунды после
импульса накачки отмечается падение
величины
в течение первой пикосекунды после
импульса накачки отмечается падение
величины
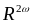 для пленок
и
и ее рост для пленки
(рис. 0.22, стрелки показывают положение
порога субпикосекундного расширения
двойного электрического слоя для
указанных образцов), обусловленные,
по-видимому, удалением нагретого
скин-слоя пленок металлов и расплава с
поверхности возбужденного кремния.
для пленок
и
и ее рост для пленки
(рис. 0.22, стрелки показывают положение
порога субпикосекундного расширения
двойного электрического слоя для
указанных образцов), обусловленные,
по-видимому, удалением нагретого
скин-слоя пленок металлов и расплава с
поверхности возбужденного кремния.
То
есть, благодаря внутреннему электрическому
полю разрушение двойного электрического
слоя происходит путем "разгрузки"
(кулоновского взрыва) неустойчивого
поверхностного слоя положительных
ионов, а уплотнение электронного газа
исчезает вследствие межэлектронного
отталкивания и электронной теплопроводности.
Сравнение значений
при
(рис. 0.19) и толщины скин-слоя
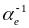 (8 12 нм) для пленок
,
и
показывает, что время разрушения двойного
электрического слоя, ограничивающее
продолжительность процесса переноса
энергии из скин-слоя в объем образца,
достаточно мало для сохранения практически
всей поглощенной энергии лазерного
излучения в плазме двойного электрического
слоя.
(8 12 нм) для пленок
,
и
показывает, что время разрушения двойного
электрического слоя, ограничивающее
продолжительность процесса переноса
энергии из скин-слоя в объем образца,
достаточно мало для сохранения практически
всей поглощенной энергии лазерного
излучения в плазме двойного электрического
слоя.
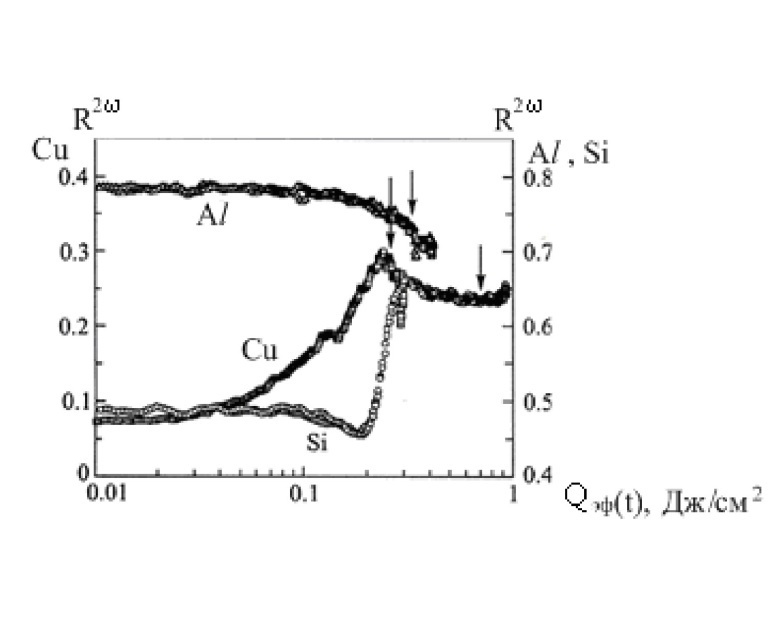
Рис.
0.22. Зависимости коэффициента отражения
(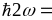 3,12эВ,
нормальное падение) от эффективной
плотности энергии
накачки для образцов
,
и
и задержек от начала импульса накачки
соответственно 0,3, 0,5 и 0,5 пс
3,12эВ,
нормальное падение) от эффективной
плотности энергии
накачки для образцов
,
и
и задержек от начала импульса накачки
соответственно 0,3, 0,5 и 0,5 пс
Таким образом, на основании полученных экспериментальных данных можно выдвинуть предположение, что при сильном неоднородном нагреве скин-слоя проводящих материалов в течение лазерного импульса накачки в нем распространяется "ударная" волна электронного давления, создающая тонкий слой сверхплотного (1023 1025см-3) вырожденного электронного газа в области границы скин-слоя под "поверхностным" слоем положительных ионов. Возникающий при этом поверхностный двойной электрический слой разрушается вследствие кулоновского взрыва и электронной теплопроводности в течение одной пикосекунды.
В заключение, говоря о механизмах лазерной абляции, следует отметить, что некоторые из них (тепловая модель, газодинамическая модель, двухтемпературная модель) получили надежное экспериментальное подтверждение. Возможность реализации других механизмов, например фотофизического, продолжает оставаться предметом теоретических и экспериментальных исследований.
