0.3.1. Нетермическое плавление

Приведем результаты экспериментов по воздействию фемтосекундных лазерных импульсов с длиной волны ( 1,56 эВ) на нелегированный кремний , в которых обнаружено плавление во время воздействия лазерного импульса длительностью 100 фс.

В эксперименте получены зависимости коэффициента самоотражения излучения накачки ( ) для - и -поляризаций от его энергии, а также временная динамика отражения зондирующего излучения ( ) при фиксированной максимальной плотности энергии p-поляризованного излучения накачки. Распределение интенсивности, построенное по изображению образца кремния в отраженном свете пробного импульса для ряда задержек относительно импульса накачки, нормировались программным образом на распределение интенсивности изображения невозбужденного образца. После калибровки было получено двумерное распределение коэффициента отражения образца, симметричное относительно центра пятна излучения накачки. Характеристики канала зондирования позволяли исследовать динамику изменения отражательной способности мишени с пространственным разрешением 2 мкм и временным разрешением около 100 фс.

Поскольку длительности пробного импульса и импульса накачки практически совпадают, то для получения временного разрешения выше 100 фс для малых задержек (100  100 фс) вычислены усредненные коэффициенты отражения . Для этого применена процедура усреднения коэффициента отражения для зондирующего излучения в пределах длительности пробного импульса (Т-преобразование) при этом форма пробного импульса приближенно принята прямоугольной с шириной 100 фс на уровне 0,5 мощности реального импульса.

Измеренные зависимости коэффициентов самоотражения излучения накачки для обеих поляризаций ( и ) от энергии импульса накачки были обработаны с использованием пространственного преобразования, устраняющего усреднение этих коэффициентов вследствие неоднородности плотности энергии в световом пятне на мишени (нормальное распределение с параметрами 73 мкм и = 43 мкм). Отражение, рассчитанное по вертикальным сечениям нормированных изображений, проведенных через центр пятна излучения накачки на поверхности образца, после приведения пространственных координат характеризуют зависимости от интегральной .

Результирующие зависимости и представлены на рис. 0.15 как функции эффективной (интегральной за импульс) плотности энергии излучения накачки . Такое представление позволяет соотнести на одном рисунке участки кривых и , отвечающие одинаковым условиям возбуждения образца.

Полученные зависимости и имеют в области малых 0,15 Дж·см^-2 один широкий минимум для р-поляризации и два совпадающих с ним узких минимума для -поляризации и проявляют резкий рост при более высоких значениях (рис. 0.15). Зависимость от , показанная на рис.0.16 жирной линией, также имеет в указанной области при тех же значениях два небольших минимума с предшествующими максимумами.

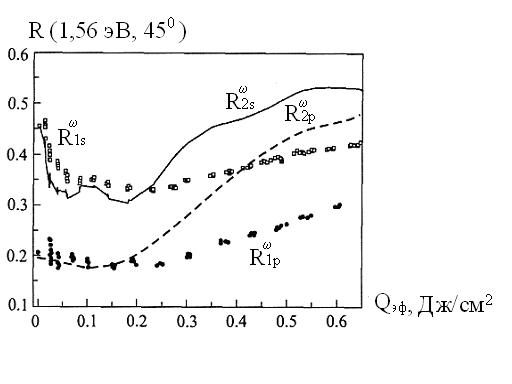
Рис. 0.15. Зависимости коэффициента самоотражения для - и -поляризованного излучения накачки: и от ; и от

Предполагается, что в течение импульса накачки здесь зарегистрированы обе полосы межзонного поглощения Si с максимумами полос, соответственно, на 3,4 и 4,3 эВ. Инициирование "красного" сдвига происходит за счет двухфотонного поглощения, сменяющегося интенсивным линейным поглощением при уменьшении ширины запрещенной зоны .

Рис. 0.16. Зависимости коэффициента отражения для пробного излучения второй гармоники от для различных задержек пробного импульса: кривые 1, 2 - (исходная) и (после T-преобразования) при нулевой задержке пробного импульса; кривая 3 -зависимость для задержки пробного импульса 200 фс; кривая 4 - зависимость для задержки 100 пс. Пик на кривой 4 соответствует коэффициенту отражения области расплава кремния, не подвергшейся абляции

С использованием зависимостей и были рассчитаны значения оптических констант и возбужденного при различных (рис. 0.16). Расчеты проведены по формулам Френеля путем подбора пар значений и , дающих минимальное отклонение расчетных значений и от экспериментальных.

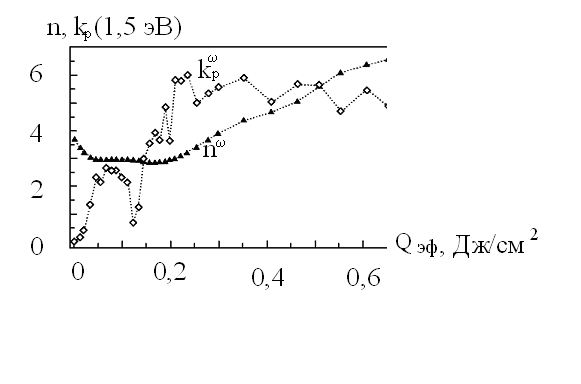
Рис. 0.17. Зависимости действительной и мнимой частей показателя преломления от мгновенной эффективной плотности энергии

В области 0,23 Дж/см² (рис. 0.16) рассчитанные значения и соответствуют оптическим постоянным равновесной жидкой фазы : (1,5 эВ) = 3,3, (1,5 эВ) = 5,7. Это значит, что превышение порога 0,23 Дж/см² приводит к сверхбыстрому нетермическому плавлению вещества в течение лазерного импульса (скачок и на рис. 0.15). Соотношение порогов термического плавления 0,16 Дж/см² (пик кривой для 100 пс на рис. 0.16) и нетермического плавления 0,23 Дж/см² составляет, примерно, 1,5, что соответствует аналогичным данным для и .

Отметим, что при 0,23 Дж/см² кривая для задержки 0 фс имеет дополнительный минимум (рис. 0.16) по сравнению с кривыми и на рис. 0.15. Эту особенность можно объяснить переходом "металл – диэлектрик" вблизи плазменной частоты холодного металлического расплава при условии . Наконец, в диапазоне 0,5 Дж/см² для кривой на рис. 0.16, как и для кривых и на рис. 0.15, отмечается насыщение отражения, в данном случае – на уровне 0,66, отвечающем коэффициенту отражения равновесного термического расплава при задержке 100 пс и его неравновесного расплава при 200 фс (рис. 0.16). Указанное плато , и соответствует "резистивно насыщенной" жидкой фазе , для которой ( – характерное время электрон-электронных соударений).

Непрерывное уменьшение 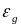для полос межзонного поглощения Si с максимумами на 3,4 и 4,3 эВ с ростом , проявляющееся в последовательном появлении обеих полос, может быть вызвано как электронными, так и структурными эффектами. Верхняя оценка плотности электронно-дырочной плазмы для "синего" края полос ~ 0,1 и 0,2 Дж/см² из условия равенства скоростей оптической генерации носителей и оже-рекомбинации ( =410^-31 см⁶/с), то есть для верхнего предела применимости Т-преобразования, для соответствующих значений и коэффициента поглощения возбужденного (данные рис. 0.16) согласно выражению

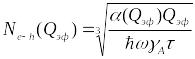(0.10)

составляет, соответственно, 1,410²² и 210²² см^-3. Эти плотности электронно-дырочной плазмы удовлетворяют как условию коллапса запрещенной зоны шириной  3 – 4 эВ – благодаря экранированию ионного остова и многочастичным взаимодействиям в электронно-дырочной плазме, так и условию дестабилизации решетки . В последнем случае непрерывное уменьшение по направлению (или ) в течение лазерного импульса может быть объяснено непрерывным ростом межатомного расстояния, происходящим, как показывает мгновенное образование "оптически толстого" слоя расплава, практически одновременно в пределах скин-слоя. Такое движение обусловлено наличием соответствующих "мягких" продольных оптических мод. Наличие "мягкой" моды является признаком структурного фазового перехода 2-го рода из метастабильной алмазной структуры возбужденного , по-видимому, в орторомбическую структуру полуметалла ( = 0) и далее с ростом – в разупорядоченную жидкую металлическую фазу. Следует отметить, что описанные явления были обнаружены также для образца .

Таким образом, экспериментально обнаружены эффекты последовательного "схлопывания" запрещенной зоны по направлениям и с последующим образованием "холодной" металлической жидкой фазы, происходящие в течение лазерного импульса длительностью 100 фс.

Экспериментально показано также, что при действии фемтосекундных импульсов с высокими интенсивностями в полупроводниках происходит сверхбыстрое плавление за времена порядка 100 фс. Так как такой тип плавления не требует нагрева решетки, поэтому его часто называют нетермическим плавлением. В металлах также может произойти такое плавление из-за деформации решетки, возникающей в результате влияния газа горячих электронов, однако в экспериментах с алюминием его признаков не обнаружено. Предполагается, что механизм нетермического плавления – это возникающая при возбуждении плотной электронно-дырочной плазмы с высокой концентрацией носителей неустойчивость кристаллической решетки.