0.0. Двухтемпературная модель при сверхкоротком воздействии

При взаимодействии сверхкоротких лазерных импульсов с проводниками процесс традиционно исследуется в рамках двухтемпературной модели, рассматривающей раздельно электронную и фононную подсистемы вещества в масштабе характерного времени электрон-фононного взаимодействия (порядка пикосекунд для большинства металлов). Подавляющее большинство экспериментальных работ, связанных с изучением характерных параметров данной модели - времен электрон-электронной релаксации и термализации электронного газа, постоянной электрон-фононного взаимодействия, а также транспорта энергии в проводнике путем баллистического разлета горячих электронов и электронной теплопроводности, проводится при низких плотностях энергии нагревающего излучения – не выше 10 мДж/см², что соответствует пиковым температурам электронного газа порядка 10⁴ К, то есть значительно ниже характерной температуры Ферми ~10⁵ К.

Проведенные впоследствии исследования динамики электрон-фононного взаимодействия (на основании решения кинетического уравнения) подтвердили правильность основных идей двухтемпературной модели и позволили определить константу электрон-фононного взаимодействия и выразить некоторые кинетические коэффициенты через микроскопические характеристики металлов.

Двухтемпературная модель описывает перенос энергии внутри металла с помощью связанных уравнений теплопроводности для температуры электронов и решетки (фононов) :

, (0.0)

. (0.1)

Здесь и 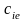– удельные теплоемкости [Дж/см³К] электронов и решетки, и – соответствующие коэффициенты теплопроводности, параметр характеризует скорость обмена энергией [Вт/см³К] между электронной и решеточной подсистемами ( – характерное время теплообмена между электронами и решеткой).

Поглощение электронами лазерной энергии описывается с помощью источника

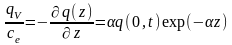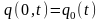, , (0.2)

где – интенсивность поглощенного излучения на поверхности металла ( ). Величина 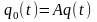в (0.2) зависит от формы лазерного импульса и поглощательной способности вещества.

Уравнения теплопроводности (0.0) и (0.1) записаны в системе координат, связанной с фронтом абляции, который распространяется относительно неподвижного вещества со скоростью . Приведенная форма удобна для анализа стационарной волны испарения.

Граничные условия представляют потоки мощности на поверхности .

Поток, определяемый потерями на эмиссию электронов:

(0.3)

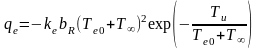– закон Ричардсона, (0.4)

где – постоянная Ричардсона, – работа выхода. Множитель в (0.4) используется для преобразования плотности потока энергии в единицы [Вт/см²].

Тепловой поток, связанный с потерями энергии на удаление вещества (абляцию), дается формулой:

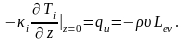(0.5)

Два других граничных условия (при ) и начальные условия (при ) очевидны:

(0.6)

Индекс "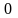 " используется для обозначения температуры на поверхности , т.е. , . Величина входит в закон Ричардсона, а величина 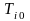определяет скорость лазерной абляции, которая записывается так:

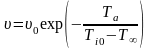. (0.7)

Для того чтобы модель была пригодна к анализу экспериментальных данных, необходимо учесть температурные зависимости коэффициентов , , , , , и 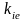. Например, электронная теплоемкость линейно зависит от электронной температуры: . Решеточная теплоемкость практически постоянна при температурах выше дебаевской температуры . Однако, если в расчетах учитываются плавление и другие структурные фазовые переходы, то эффективная решеточная теплоемкость зависит от температуры решетки . Электронная теплопроводность зависит от температур и . Коэффициенты отражения и поглощения также в общем случае зависят от температур и . В полупроводниках коэффициент отражения изменяется линейно с электронной температурой .

Для того чтобы проиллюстрировать основные особенности двухтемпературной модели, рассмотрим упрощенную задачу, в которой все коэффициенты считаются постоянными.

Следует отметить, что двухтемпературная модель (0.0) и (0.1) применима в случае, когда можно использовать классические законы Фурье для описания переноса тепловой энергии электронов и фононов. Это означает, что модель применима для времен, много больших, чем характерное время установления равновесного распределения в электронном газе. Время зависит от электронной температуры и обычно составляет десятки - сотни фемтосекунд. Кроме того, предположение, связанное с диффузионным переносом электронной энергии (0.0), подразумевает, что характерные вариации в распределении электронной температуры возникают на пространственных масштабах, больших, чем длина свободного пробега электрона . На более коротких длинах перенос электронов в основном баллистический. Величина 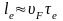(где – фермиевская скорость электронов) для различных металлов меняется более чем на порядок (для никеля длина свободного пробега электронов составляет несколько десятков нанометров, в то время как для золота она составляет сотни нанометров).

Когда время релаксации 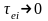( ), двухтемпературная модель переходит в тепловую модель с единой температурой твердого тела , при этом величины и представляют собой полные теплоемкость и теплопроводность твердого тела.

В случае лазерного фемтоимпульса возникает большая разница в характеристических временах нагрева электронов и решетки, тогда как абляция обычно начинается после лазерного импульса.

Расчеты с помощью упрощенной двухтемпературной модели (см. раздел 1.2.1), в которой не учтены конвективные члены , не позволяют определить толщину слоя материала, удаленного в результате воздействия лазерного импульса. Для таких расчетов необходимо использовать полную модель (0.0), (0.1) и, кроме того, вести расчет до времен порядка 10³ длительности лазерного импульса.

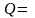Динамика нагрева металла лазерным импульсом с длительностью 1 пс и плотностью энергии в импульсе 0,15 Дж/см² представлена на рис. 0.0. Форма импульса моделировалась функцией

(0.8)

параметры расчета: =0,04035 Дж/см³К, =2,43 Дж/см³К, =2,37 Вт/смК, =1 Вт/смК, время релаксации =1 пс ( ), плотность =2,688 гсм^-3, скрытая теплота испарения =10860 Дж/г, множитель в (0.7) =414000 см/с, энергия активации =35240 К, работа выхода в (0.4) 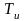=49300 К, постоянная Ричардсона =120,4 А/см²К², начальная температура =300 К, коэффициент поглощения =1,51610⁵ см^-1, поглощательная способность .

Из рис. 0.0, видно, что в течение лазерного импульса электронная температура 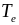"отрывается" от решеточной температуры и достигает максимума в момент 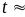1,8 пс. Характерное время нагрева решетки существенно больше (это следует из соотношения 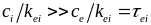); фононная температура достигает максимума при 27,2 пс.

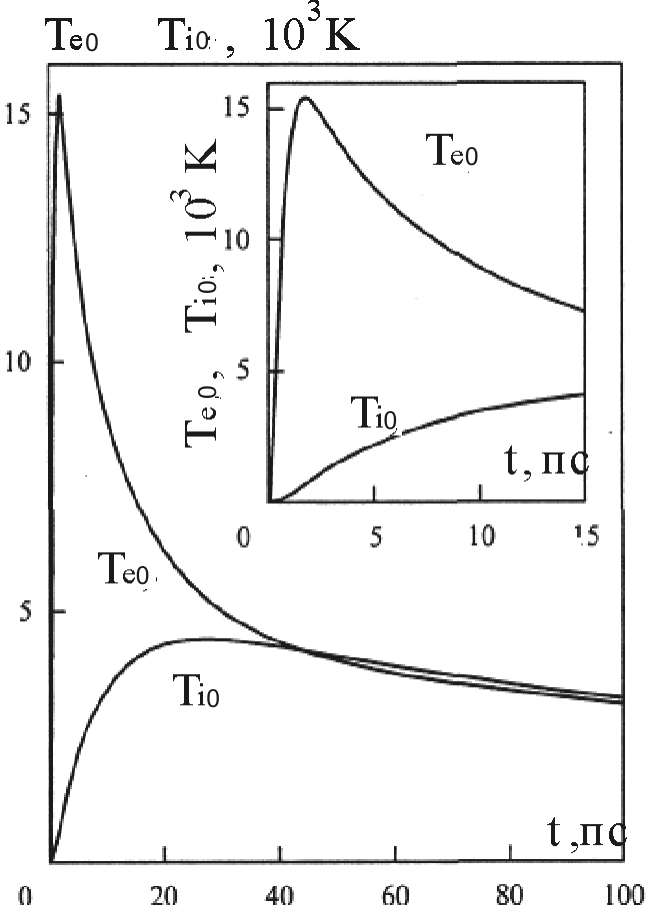
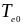Рис. 0.0. Динамика воздействия на металл лазерным импульсом с длительностью = 1 пс и плотностью энергии в импульсе = 0,15 Дж/см², электронная и решеточная температуры и (на вставке – увеличенное изображение начальной стадии процесса)

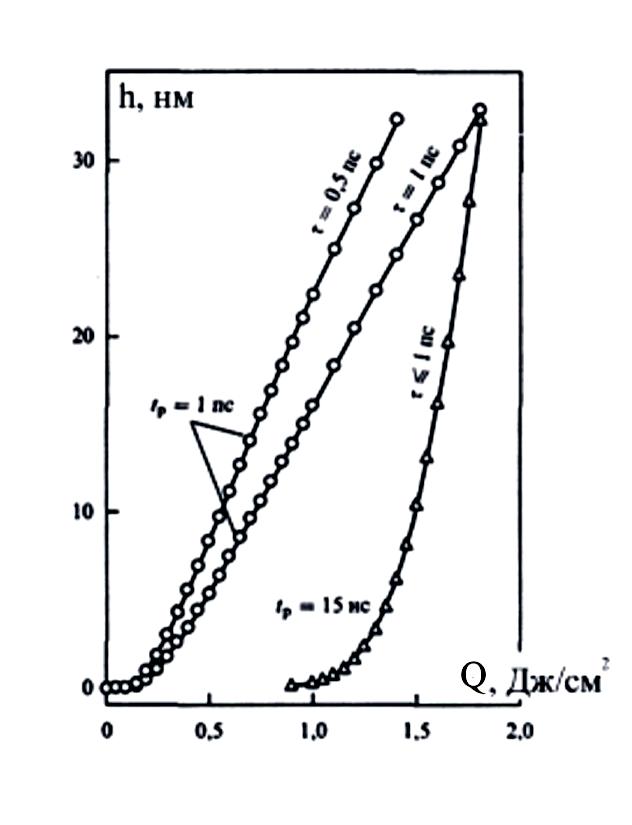
Эффект зависимости кинетики абляции от длительности лазерного импульса иллюстрирует рис. 0.1б, откуда следует, что для наносекундного лазерного импульса абляция нечувствительна к скорости обмена энергией между решеткой и электронами. При 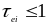пс кривые совпадают с результатами, следующими из чисто тепловой модели абляции с единой температурой электронов и решетки. Для пикосекундных лазерных импульсов соответствующие кривые чувствительны к характерному времени релаксации 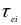. 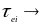При 0 (случай чисто тепловой модели) кривые демонстрируют слишком быстрый рост толщины аблированного слоя по сравнению с экспериментальными зависимостями.

Из рис. 0.1б следует и другой известный эффект – уменьшение порога абляции при укорочении лазерного импульса.

Таким образом, двухтемпературная модель правильно описывает основные закономерности абляции, тогда, когда переход из твердой фазы в газообразную происходит поэтапно: нагревание, плавление, испарение. Отличие в том, что в условиях мгновенного нагрева вместо обычной задачи о распространении фронта абляции следует решать более простую задачу об адиабатическом разлете предварительно нагретого слоя вещества.

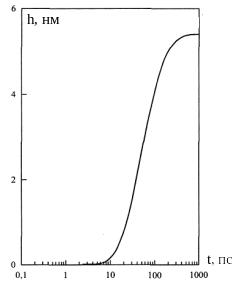
Детальный анализ процесса разлета можно провести на основе экспериментальных данных, подобных приведенным в разделе Рис. 0.1. а – толщина удаленного материала как функция времени (длительность импульса =1 пс, плотность энергии в импульсе =500 мДж/см2), б – толщина удаленного за импульс материала как функция плотности энергии в импульсе для одного длинного и двух коротких лазерных импульсов.

а б

Рис. 0.1. а – толщина удаленного материала как функция времени (длительность импульса =1 пс, плотность энергии в импульсе =500 мДж/см²), б – толщина удаленного за импульс материала как функция плотности энергии в импульсе для одного длинного и двух коротких лазерных импульсов