0.2.2. Нагрев металла импульсным излучением постоянной мощности
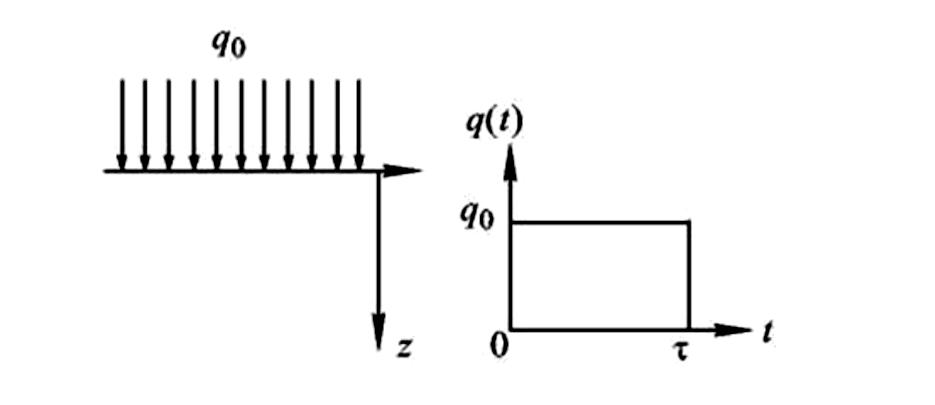
Рис. 0.13. Нагрев металла импульсным излучением постоянной мощности
Если область тепловыделения мала, то все источники можно перенести на границу:
(0.44)
Решение
этого уравнения при
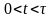будет:
,
(0.45)
а температура поверхности
(0.46)
Выражения
(0.45),
(0.46)
часто используются в оценках режимов,
при которых должна достигаться заданная
температура поверхности
.
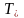Поток
,
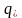необходимый для достижения температуры
к моменту окончания импульса длительностью
,
будет
,
обратно пропорционален корню квадратному из длительности импульса
,
а вложенная за время импульса энергия, необходимая для достижения поверхностью температуры , пропорциональна корню квадратному из длительности импульса
.
Определим
изменение температуры при остывании
полупространства после окончания
импульса излучения. Зная, как нагревается
полупространство постоянным во времени
излучением, включим в момент окончания
импульса отрицательный поток лазерного
излучения (см. стр. 52). Тогда одномерное
температурное поле полубесконечного
тела от действия источника тепла
постоянной интенсивности длительностью
может быть представлено для
в виде
(0.47)
Отсюда
для скорости охлаждения
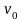поверхности
после окончания действия импульса
получим
Выражение для градиента температуры при нагреве полупространства поверхностным источником тепла с постоянной интенсивностью получим, дифференцируя по функцию, описываемую уравнением (0.45),
.
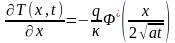Для
определения
можно использовать линейную аппроксимацию,
причем размер прогретого слоя определяется
в этом случае довольно строго:
Если тепловой поток зависит от времени, то температура поверхности будет:
.
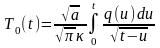(0.48)
0.2.3. Нагрев материала лазерным пучком с гауссовым профилем
Особенностью задач, связанных с нагревом материалов лазерным излучением является то, что распределение излучения и, следовательно, тепловой источник, как правило, обладает резко изменяющимися пространственно-временными характеристиками. Поэтому идеализация свойств тепловых источников, часто допускаемая в расчетных схемах для уменьшения математических трудностей, может приводить к отклонениям расчетных данных от экспериментальных.
Временная
структура импульса зависит от типа
лазера и особенностей режима генерации
излучения. В самом общем виде распределение
плотности мощности лазерного излучения
на поверхности материала является
сложной функцией координат и времени
.
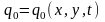С некоторым приближением структуру
распределения
можно представить в виде произведения
функции, зависящей только от времени,
на функцию координат поверхности:
,
(0.49)
где
поглощательная
способность, в общем случае зависящая
как от состояния (степени обработки)
поверхности, так и от ее температуры;
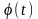описывает временную
структуру импульса;
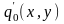пространственное
распределение плотности мощности
падающего лазерного излучения.
Если неоднородности в лазерной системе малы, то после фокусирующей системы распределение можно описать дифракционной кривой. Конечно, в реальных условиях распределение мощности излучения отлично от неё. Это связано с неоднородностью распределения фазы и амплитуды лазерного излучения по торцу активного элемента вследствие генерации многих видов колебаний оптического резонатора, несимметрии возбуждения, оптического несовершенства кристалла и т.д. Поэтому целесообразно использовать при рассмотрении процессов нагрева лазерным излучением более простую математическую аппроксимацию реальной пространственной структуры лазерного импульса – закон нормального распределения или равномерное по пятну фокусировки значение . Следует заметить, что пространственно-временная структура импульса излучения не всегда может быть аппроксимирована выражением (0.49).
Проанализируем теперь процесс лазерно-индуцированного нагрева материала методом функции Грина с учетом теплового размытия зоны воздействия по поверхности. Предполагаем, что лазерный пучок, падающий на поверхность x,y, имеет гауссов профиль и распространяется вдоль оси z
(0.50)
где — радиус гауссова светового пучка.
Для получения качественных представлений о нагреве материала непрерывным лазерным излучением достаточно моделировать временной ход оптического воздействия ступенчатой функцией Хевисайда (см. рис. 0.14):
(0.51)
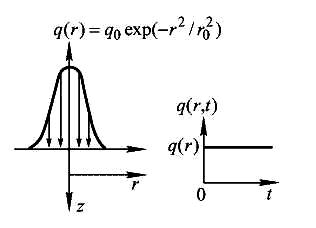
а б
Рис. 0.14. Пространственное (а) и временное (б) распределение потока падающего лазерного излучения
Из уравнения (0.13) можно получить удобную для анализа аналитическую зависимость скорости нагрева полупространства непрерывным лазерным пучком, в котором пространственно-временное распределение интенсивности описывается выражениями (0.50, 0.51)
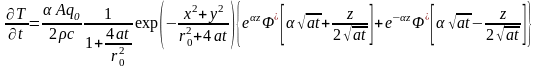
Как и
следовало ожидать, максимальный темп
роста температуры наблюдается на
поверхности (
)
облучаемого материала на оси лазерного
пучка (
).
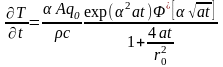(0.52)
Согласно
(0.52),
на начальном этапе воздействия процессы
теплопроводности не влияют на скорость
нагрева, которая в этом случае не зависит
от времени. Поэтому можно ввести два
характерных времени:
– время, за которое влияние источника
тепловыделения распространяется на
расстояние порядка
,
и
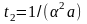– время, по истечении которого глубина
проникновения лазерного излучения в
вещество скажется на нагреве поверхности.
Как следует из (0.52),
при
максимальная температура материала
растет с течением времени по линейному
закону
.
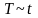С
увеличением времени нагрева начинают
сказываться процессы теплопередачи
вглубь среды, при этом темп нагрева
замедляется. При условии
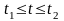соотношение (0.52)
принимает вид
,
.
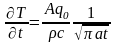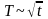С
увеличением времени воздействия (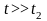
),
темп роста температуры ещё более
замедляется за счёт включения механизмов
теплопередачи вдоль поверхности,
происходит “размытие” границ зоны
термического влияния:
.
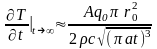Установление температурного поля происходит по закону
.
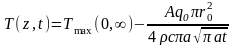(0.53)
Максимальная температура определяется формулой
,
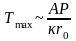где
- полная мощность лазерного пучка с
радиусом
и интенсивностью на оси
.
В случае слабопоглощающих материалов
(
)
замедление темпа нагрева начинается
при временах
.
При
.
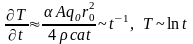При
дальнейшем увеличении времени воздействия
(
)
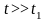начинает играть роль поверхностное
размытие пятна нагрева за счет
теплопроводности. Поэтому справедливы
оценки по (0.53),
что в пределе при
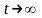и
дает
.
Из
приведенных формул ясно, что для
достижения максимальной температуры
нагрева материала при фиксированных
пространственных и энергетических
параметрах
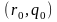лазерного пучка необходимо использовать
лазерные источники, которые лучше
поглощаются в материале. При фиксированных
же
и
увеличение максимального нагрева можно
добиться путем фокусировки лазерного
пучка, т.е. уменьшения
.