0.2.1. Нагрев полупространства экспоненциально спадающим с глубиной тепловым источником

Предположим, что на металл, поглощательная способность которого не зависит от температуры, падает лазерное излучение, плотность потока которого равномерно распределена по пятну нагрева радиуса

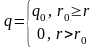
и не зависит от времени.

Для получения качественных представлений о нагреве материала непрерывным лазерным излучением достаточно моделировать временной ход оптического воздействия ступенчатой функцией Хевисайда:

Выявление основных закономерностей процесса удобно проводить для одномерных моделей, применение которых справедливо при 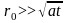. Практически все начальные стадии нагрева металлов как импульсным, так и непрерывным излучением можно рассматривать в одномерном приближении, представляя металл полупространством (рис. 0.12), т.е. 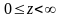, объемный источник тепла будет ( 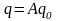). Считаем, что 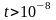с, то есть .

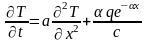(0.37)

Начальное условие (0.5) запишем для равномерного распределения температуры в теле: 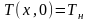(в большинстве случаев можно считать 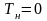). Тогда, когда процесс нагревания определяется абсолютной температурой, считать нельзя, если процесс реагирует на перепад температуры, то можно принять .

Граничные условия (0.7) описывают поведение температуры на большом удалении от облучаемой поверхности

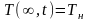(0.38)

На облучаемой поверхности действуют граничные условия II рода (0.8) при

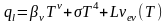
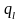- теплопотери (отрицательные по величине), первый член – потери конвекционные, при 1000 К ~10 Вт/см², второй член – лучистые потери, при 1000 К ~5 Вт/см², последний член – потери на испарение, наиболее существенный, в определенных условиях могут компенсировать ввод тепла полностью. На стадии, когда разрушения вещества нет (скорость испарения мала), этим членом пренебрегают.

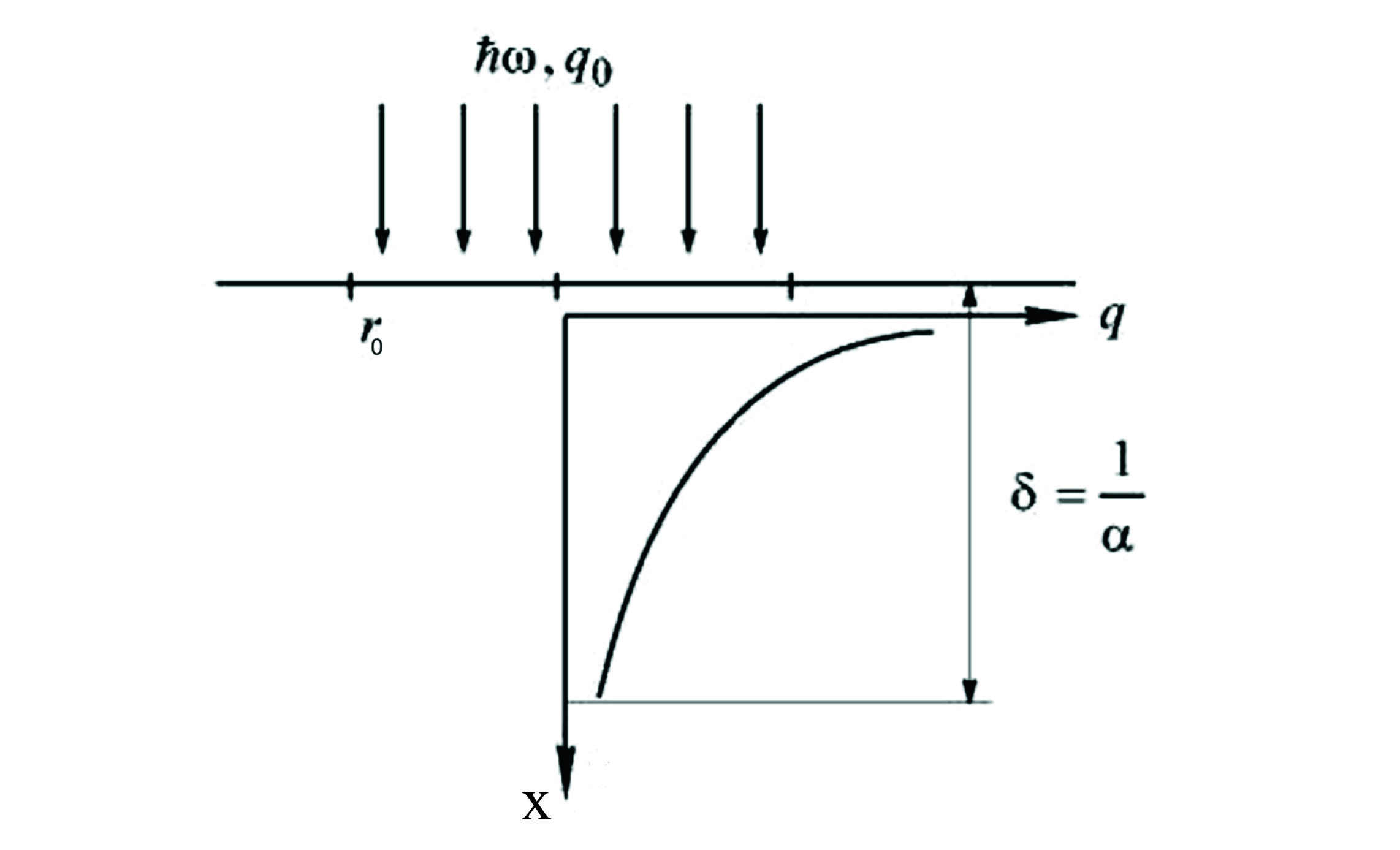
Рис. 0.12. К постановке краевой задачи теплопроводности при выравнивании температур и

Таким образом, в большинстве случаев поверхность, на которую падает лазерное излучение, можно считать теплоизолированной. Поэтому граничные условия на поверхности выглядят так:

,

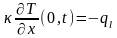следовательно, при малых потерях

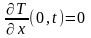. (0.39)

Применив преобразования Лапласа (0.11) к уравнению (0.37) и граничным условиям (0.38, 0.39), получим дифференциальное уравнение в полных дифференциалах для рассматриваемой краевой задачи

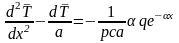(0.40)

В (0.40) учтено, что 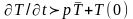, кроме того, 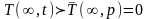и 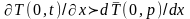. Условия (0.38, 0.39) приобретают вид:

, .

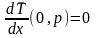При этих условиях решение (0.40) будет:

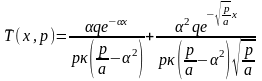
Воспользовавшись таблицами обратных преобразований, получим распределение температуры в глубь металла:

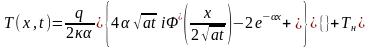. (0.41)

Весь разогрев определяется соотношением трех величин, имеющих размерность длины: - координата, - глубина проникновения излучения, - длина теплопроводности (то есть расстояние, на которое уходит температурная волна от места, в котором она образовалась).

Проанализируем выражение (0.41). При 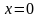получим выражение для температуры на поверхности:

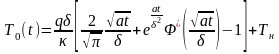(0.42)

После окончания воздействия длительностью для нахождения температуры на поверхности можно воспользоваться понятием стока. Под стоком понимают источник тепла с отрицательной интенсивностью, равной интенсивности источника, включенный на время позднее источника.

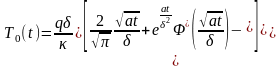
Частные случаи:

1) Теплопроводность еще не работает – , ( ),

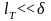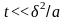(0.43)

весь разогрев определяется тепловыделением на глубине .

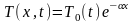
Если тепловой поток является функцией времени, то 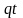следует заменить на 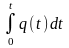. Для металлов это приближение справедливо при временах 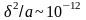с. При этих временах для металлов можно говорить только о температуре электронов . Для диэлектриков, когда может быть 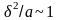, выражение (0.43) справедливо почти всегда.

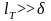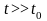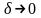В тех случаях, когда теплопроводность играет определяющую роль в распределении температуры ( ), что характерно для большинства случаев лазерного воздействия на металлы, распределение температуры можно получить из (0.41) при . Но можно специально решить задачу о нагревании полупространства при поглощении лазерного излучения на границе.