2 курс / Л-5.1 (2) Квантові властивості випромінювання

ЕЛЕМЕНТИ АТОМНої і КВАНТОВої ФІЗИКи

І. Квантові властивості випромінювання

1 Теплове випромінювання. Абсолютно чорне тіло. Закон

Кірхгофа для теплового випромінювання

Теплове випромінювання – це електромагнітне випромінювання атомів і молекул, збуджених за рахунок теплової енергії. Воно має місце при будь-якій температурі, відмінній від абсолютного нуля.

Тіла можуть світитись не тільки за рахунок теплової енергії. Це різні види люмінесценції: хемілюмінесценція–свічення за рахунок енергії хімічної реакції; катодолюмінесценція–свічення кристалофосфорів при бомбардуванні електронами (екрани телевізорів, монітори); фотолюмінесценція–свічення фосфорів при освітленні; електролюмінесценція–свічення кристалів у електричному полі; тріболюмінесценція–свічення при руйнуванні кристалу і т.д. Але всі вони нерівноважні. Тому люмінесценцію називають холодним свіченням.

Потік випромінювання Ф, який падає на поверхню твердого тіла, може бути: 1) відбитий Ф_ρ; 2) поглинутий Ф_α; 3) пройти Ф_τ (див. рисунок). Кожний із цих процесів характеризується відповідним коефіцієнтом:

Відбивання , поглинання 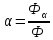і пропускання 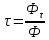, які показують відносну долю кожного процесу. Очевидно, що 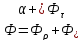, а тому сума коефіцієнтів дорівнює одиниці . Всі ці коефіцієнти залежать від температури та довжини хвилі. Залежністю від довжини хвилі пояснюються різні кольори тіл. У відбитих променях тіло має той колір, довжину хвилі якого відбиває це тіло.

Якщо тіло поглинає випромінювання всіх довжин хвиль, тобто , а 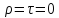, то таке тіло називається абсолютно чорним. Якщо ж 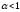і не залежить від довжини хвилі, тіло називається сірим. Абсолютно чорних тіл, як і других ідеальних об’єктів, у природі не існує. Найкращим наближенням до абсолютно чорного тіла є замкнута порожнина (див. рис.), в стінці якої зроблений невеликий отвір. Випромінювання, що потрапило в порожнину, зазнає багатократного відбивання і практично не може вийти з порожнини. Це означає, що коефіцієнт поглинання такої системи дорівнює одиниці, як і у абсолютно чорного тіла. Якщо нагріти оболонку до деякої температури, то із отвору буде виходити випромінювання таке ж як і від абсолютно чорного тіла з такою ж температурою і з площі, яка дорівнює площі отвору.

Інтегральною густиною випромінювання R_Т називається енергія, яка випромінюється з одиниці площі нагрітого тіла за одиницю часу у всьому можливому інтервалі довжин хвиль (від 0 до ∞)

(1)

Індекс Т означає, що інтегральна густина випромінювання залежить від температури і розраховується (вимірюється) при сталій температурі.

Експерименти показують, що енергія випромінювання розподілена по довжинам хвиль нерівномірно. Тому вводиться ще одна характеристика теплового випромінювання – спектральна густина випромінювання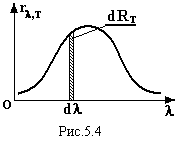

,

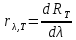яка дає енергію випромінювання з одиниці площі за одиницю часу в нескінченно малому інтервалі довжин хвиль, біля хвилі певної довжини. Тоді одиниця спектральної густини випромінювання

.

Очевидно, що інтегральна густина випромінювання

(2)

це площа під кривою спектральної густини випромінювання (див. рисунок).

У 1859 р. німецький фізик Г. Кірхгоф (1824-1887) експериментально встановив закон, який дає зв’язок між випромінювальною і поглинальною здатністю тіл – закон Кірхгофа:

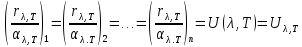. (3)

Відношення спектральної густини випромінювання до коефіцієнта поглинання, при однаковій довжині хвилі і температурі, для різних тіл однакове і є універсальною функцією довжини хвилі і температури .

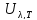З’ясуємо фізичний зміст цієї функції. При , тобто для абсолютно чорного тіла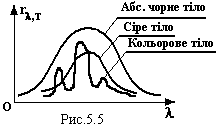

, (4)

– це функція спектральної густини випромінювання абсолютно чорного тіла.

Для будь-якого іншого тіла спектральна густина випромінювання . А так як , то 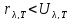, тобто будь-яке тіло при будь-якій довжині хвилі випромінює менше енергії, ніж абсолютно чорне тіло (див. рис.).

2 Розподіл енергії в спектрі абсолютно чорного тіла.

Формули Віна, Релея-Джинса, Планка

У 1893 р. німецький фізик В.Він (1864-1928) з термодинамічної точки зору рівноважного теплового випромінювання одержав розподіл енергії в спектрі абсолютно чорного тіла. Формула Віна Має вид

, (5)

а і b – константи.

У 1900 р. англ. фізики У.Релей і А.Джинс на основі класичних уявлень про випромінювання, а саме: неперервний характер випромінювання та рівномірний розподіл енергії по степеням вільності, також одержали формулу розподілу енергії у спектрі абсолютно чорного тіла

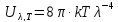. (6)

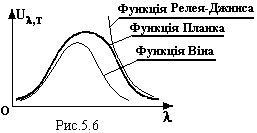
Але ні один із цих законів не узгоджувався з експериментальною кривою в усьому діапазоні довжин хвиль (див. рисунок). Формула Віна (5) давала добре узгодження в області коротких довжин хвиль, а формула Релея-Джинса (6) – в області великих довжин хвиль. Більш того, формула (6) взагалі давала абсурдний результат в області коротких хвиль: при зменшенні довжини хвилі (в ультрафіолетовій області) спектральна густина випромінювання, а разом з нею і інтегральна густина, зростали до нескінченності, що з енергетичної точки зору неможливо. Це протиріччя одержало у фізиці назву „ультрафіолетової катастрофи”.

Для усунення цих недоліків у 1900 р. нім. фізик М.Планк (1858-1947) висунув гіпотезу про дискретний (квантовий) характер випромінювання: випромінювання хвиль, їх поширення і поглинання відбувається певними порціями, квантами. Енергію кванта випромінювання з частотою ν, або довжиною хвилі λ дає вираз

, (7)

де: 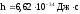- стала Планка, с – швидкість світла. Одержана Планком формула

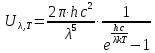(8)

повністю співпадає із експериментальною кривою розподілу енергії в спектрі випромінювання абсолютно чорного тіла (див. рис.), а граничні переходи дають формули (5) і (6). Дійсно, при малих λ одиницею у знаменнику можна знехтувати, що приводить до формули Віна

.

При великих λ: 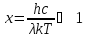. Розкладаємо експоненту в ряд, обмежившись двома першими членами, 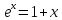. Одержуємо якісно формулу Релея-Джинса

.

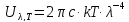3. Фотоефект. Закони фотоефекту. Рівняння Ейнштейна для фотоефекту

Першим експериментальним підтвердженням гіпотези Планка про квантування випромінювання електромагнітних хвиль виявилось явище фотоефекту. Явище фотоефекту заключається у вибиванні електронів із поверхні металів при їх опромінюванні світлом. Воно було відкрито Г.Герцем ще у 1887р. В роботах В.Гальвакса, П.Ленарда та інших були встановлені кількісні характеристики явища. Саме явище дістало назву зовнішнього фотоефекту. Лише в 1900 р. було з’ясовано, що УФ-випромінювання вибиває з металевого катоду електрони. Дослідна установка і вольт-амперна характеристика процесу зображені на рисунку:

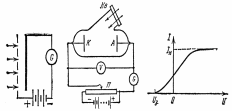
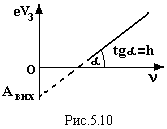
Закони Фотоефекту:

1. Кількість електронів, що вивільняються світлом за 1с (струм насичення ) прямо пропорційна величині світлового потоку, що падає на катод.

2. Швидкість вилітаючих з катода електронів тим більша, чим більша частота 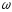падаючого світла, але вона не залежить від величини світлового потоку.

3. Незалежно від інтенсивності світла, фотоефект починається тільки при цілком певній для данного металу мінімальній частоті світла, яку називають “червоною межою” фотоефекту.

4. Явище фотоефекту фактично безінерційне. (час між падінням світла і виходом електрону із металу ).

Закони фотоефекту не знайшли пояснення в рамках класичних уявлень про хвильову природу світла. З класичної точки зору вектор електричного поля падаючої хвилі розгойдує електрони катода. Але:

1. На це потрібен час, набагато більший

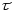
2. Вектор електричного поля тим більший чим більший світловий потік.

Чітке пояснення фотоефекту дав А. Ейнштейн у 1905р. на основі припущення, що світло є потоком матеріальних частинок – фотонів, енергія яких:

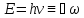
де 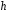- стала Планка, - частота світлової хвилі, - циклічна частота;

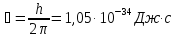
Енергія фотона повністю поглинається вільним електроном поверхневого шару металу. Застосовуючи до взаємодії фотона з електроном закон збереження енергії, Ейнштейн встановив рівняння фотоефекту:

.

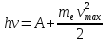А – робота виходу електрона з металу. 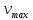- максимальна швидкість електронів після виходу з металу. Це рівняння пояснює всі закони фотоефекту.

4. Комптонівське розсіювання рентгенівського випромінюванння

(Самостійно. Реферат)

5. Імпуьс і маса фотона

Кожний фотон маючи енергію повинен мати імпульс і масу.

=.

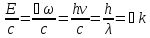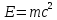- зв’язок між масою і енергією.

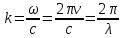- хвильове число.

с – швидкість світла; 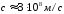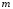_, - маса рухомого фотона.

Тоді, враховуючи, що імпульс величина векторна можна записати

де 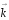- хвильовий вектор, ( ).

Фотон не має маси спокою, тобто він не може не рухатись. Він може бути поглинутий тільки повністю.