2 Расчет переходного процесса в цепи операторным методом

На вход изображенной на рисунке 2.1 схемы в момент времени t=0 подается скачок напряжения величиной U₀ = 1 B.

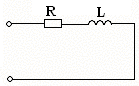
Рисунок. 2.1 - RL-цепь.

Найти зависимость входного тока i₁ от времени t при нулевых начальных условиях.

Численные значения параметров элементов схемы: R = 10 кОм, L = 100 мГн.

Операторная схема замещения электрической цепи изображена на рисунке 2.2.

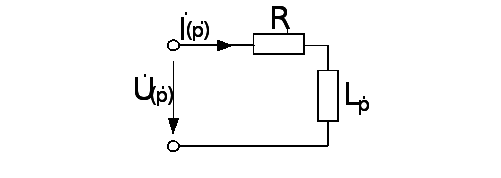
Рис. 2.2 - Операторная схема замещения цепи рисунка 2.1.

Закон Ома в операторной форме:

. (2.1)

Операторное сопротивление равна:

. (2.2)

Изображение определяется выражением:

. (2.3)

Теперь, подставим значения и в формулу (2.1), получим следующее выражение:

. (2.4)

Перейдем от изображения функции входного тока к оригиналу и подставим численные значения [5]:

(2.5)

Конечное выражение:

В таблице 2.1 представлены численные значения для построения графика изменения тока.

Таблица 2.1 – Численные значения для построения графика изменения тока

10-4 t, c	0	1	2	3	4	5	6	7	8	9	10
i1св(t), 10-5 А	0	6,32	8,64	9,5	9,8	9,93	9,97	9,99	9,99	9,99	10

На рисунке 2.3 показан график изменения тока согласно выражению (2.5) в исследуемой цепи, который был построен в Excel 2013.

Рисунок 2.3 - График тока в цепи.

Таким образом, был построен график изменения тока в RL цепи.

3 Расчет однородной двухпроводной линии без потерь

3.1 Расчет частот и входного сопротивления короткозамкнутого отрезка кабеля

В третьем разделе курсовой работы необходимо определить частоты, на которых выполняется условие резонанса токов и напряжений для замкнутого отрезка кабеля без потерь, найти входное сопротивление кабеля на частоте 100МГц.

Таблица 3.1 - Численные данные для расчета частот резонанса тока, напряжения и входного сопротивления.

Гн/км	Ф/км	,м	,МГц
		1.5	100

Входное сопротивление замкнутого отрезка кабеля длиной рассчитываетсяпо формуле (3.1):

(3.1)

здесь- волновое сопротивление кабеля; β- коэффициент фазы.

Модуль

. (3.2)

В результате того, что резонанс напряжений для отрезка кабеля наступает на тех частотах, при которых,условие резонанса напряжений записывается в виде:

. (3.3)

Так как , то:

. (3.4)

Равенство (3.4) выполняется, когда:

, k=0,1,2… (3.5)

Учитывая, что для кабеля без потерь β определяется выражением:

. (3.6)

Получаем:

. (3.7)

Выходят частоты резонанса напряжений:

. (3.8)

Подставив численные значения исходных данных в (3.8) и вычислим резонансную частоту напряжений:

. (3.9)

Далее необходимо найти частоту резонанса токов. Известно, что при резонансе токов , отсюда:

. (3.10)

Данное условие выполняется только при[6]:

, k=0,1,2… (3.11)

Подставив в данное выражение, выражение(3.6), получим:

. (3.12)

Отсюда частоты резонанса токов:

. (3.13)

Найдем входное сопротивление кабеля на частоте 100 МГц, расчёт тангенса произведён в градусах.

. (3.14)

Таким образом:

.

Таким образом, был произведён расчет частот и входного сопротивления короткозамкнутого отрезка кабеля.