Добавил:

anna4514793 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Гомельский государственный университет им. Франциска Скорины

Предмет:

Математика

Файл:

Excel / Лабораторная работа 8_

.doc

Скачиваний:

Добавлен:

24.10.2019

Размер:

674.82 Кб

Скачать

☆

ЛАБОРАТОРНАЯ РАБОТА № 9. Методы отделения и уточнения корней нелинейных уравнений.

9.1. Графический метод отделения корней

Постановка задачи. Отделить корни нелинейного уравнения графически и аналитически. Определить число действительных корней.

Решение. На интервале найдем корни уравнения

. (9.1)

а) первый способ

Для приблизительного определения интервала построения графика функции найдем точки локального экстремума данной функции . Находим первую производную . Решая уравнение , находим критические значения и . Составляем таблицу 9.1.

Таблица 9.1 – Точки экстремума

Учитывая таблицу 9.1, в качестве интервала возьмем . На нем строим график 9.1 функции .

Из рисунка 9.1 следует, что уравнение (9.1) имеет три действительных корня, расположенных на промежутках:

. (9.2)

Теперь в качестве начальных приближенных значений корней можно взять, например:

. (9.3)

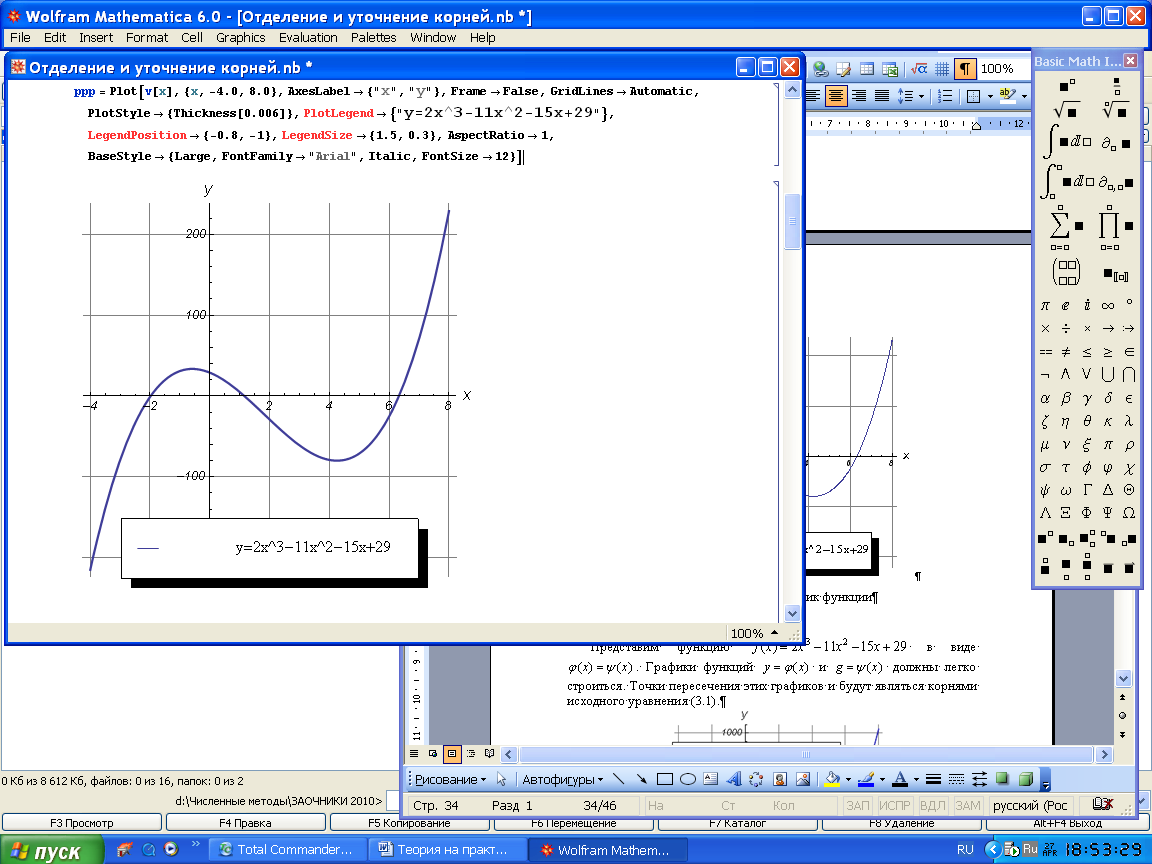
Рисунок 9.1 – График функции

б) второй способ

Представим функцию в виде . Графики функций и должны легко строиться. Точки пересечения этих графиков и будут являться корнями исходного уравнения (9.1).

Рисунок 9.2 – Пересечение графиков и

Пусть и . Построим оба графика в одной системе координат (рисунок 9.2).

Из анализа рисунка 9.2 следует, что корни уравнения (9.1) лежат на тех же промежутках (9.3).

9.2 Аналитический метод отделения корней

Для определения количества корней воспользуемся правилом Декарта: Число положительных корней уравнения (9.1) с учетом их кратностей равно числу перемен знаков в последовательности коэффициентов (причем равные нулю коэффициенты не учитываются) или меньше этого числа на четное число.

Для определения числа отрицательных корней достаточно применить правило Декарта к многочлену . Имеем последовательность коэффициентов .

В первом случае имеется две перемены знаков, значит, положительных корней будет два. Во втором случае имеем одну перемену знака, то есть один отрицательный корень.

Учитывая сведения из таблицы 9.1, составим таблицу 9.2 знаков функции

Таблица 9.2 – Таблица знаков

	-4	-2	-1		0	2		6	8
-	-	-	+	+	+	-	-	-	+	+
+	+	+	+		-	-		+	+	+

корень1 корень2 корень3

Так как данная функция является непрерывной (как сумма непрерывных функций), то из таблицы 9.2 следует, что функция меняет знак на промежутках , следовательно, уравнение (9.1) имеет три действительных корня принадлежащих этим промежуткам:

(9.4)

Эти результаты согласуются с промежутками из (9.2).

9.3 Уточнение корней уравнений

9.3.1 Метод простой итерации

Пример. Пусть требуется уточнить второй корень уравнения (9.1):

. (9.5)

Из (9.2) следует, . В методе итераций уравнение (9.5) необходимо привести к виду

причем для сходимости итераций необходимо, чтобы выполнялось условие

. (9.6)

В качестве обычно берут

, (9.7)

где – параметр. Пусть постоянного знака на отрезке . Для нахождения положим

=, .

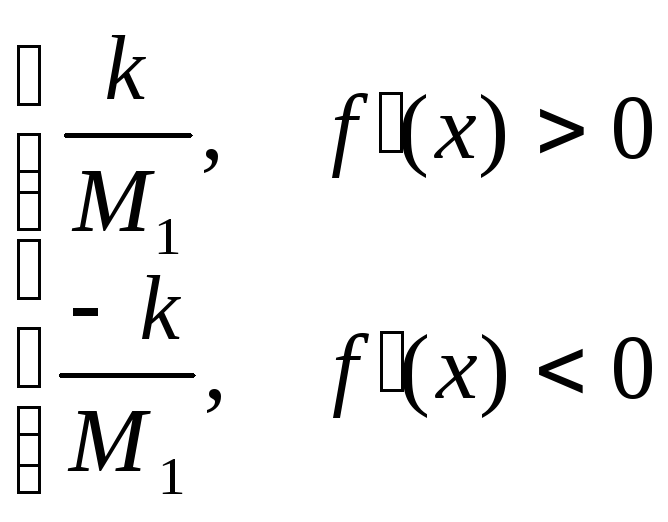Таким образом, уравнение готовое для итераций примет вид:

. (9.8)

Для того чтобы при уточнении корня необходимо было сделать меньшее число шагов для получения требуемой точности, данный интервал следует сузить до тех пор, например, методом половинного деления, пока не будет выполняться условие

, где , . (9.9)

В нашем случае и , а отрезок . Найдем минимальное и максимальное значение производной:

, .

Значит, , то есть . Поэтому данный промежуток дальше сужать не следует.

Обратим внимание, если бы взяли промежуток как в (9.4), то его надо было бы сузить, так как .

Теперь возьмем, например, и поскольку , то значение и .

Проверим условие сходимости метода итерации

Если последнее неравенство выполняться не будет, то следует взять другое значение для .

Уравнение (9.8) примет вид

. (9.10)

Итерационные вычисления проведем по формуле

. (9.11)

Процесс продолжается до тех пор, пока .

В качестве начального приближения возьмем значение . Все вычисления представлены в таблице 9.3.

Таблица 9.3 – Таблица итераций


1.5	1.155	1.15747
1.155	1.15747	1.15754
0.345< нет	0.0025< нет	0.00007< да

На третьей итерации исходная точность достигнута. Проведем проверку полученного результата: . Таким образом, уточненный корень будет: .

9.3.2 Метод хорд

Как и в методе простой итерации, уточним корень . Данный интервал удовлетворяет условию (9.9) быстрой сходимости итерационного процесса. В методе хорд решение ищется по формуле:

. (9.12)

За неподвижный конец отрезка принимается та точка, для которой знак функции совпадает со знаком второй производной: .

График функции (9.5) на отрезке имеет вид (рисунок 9.3):

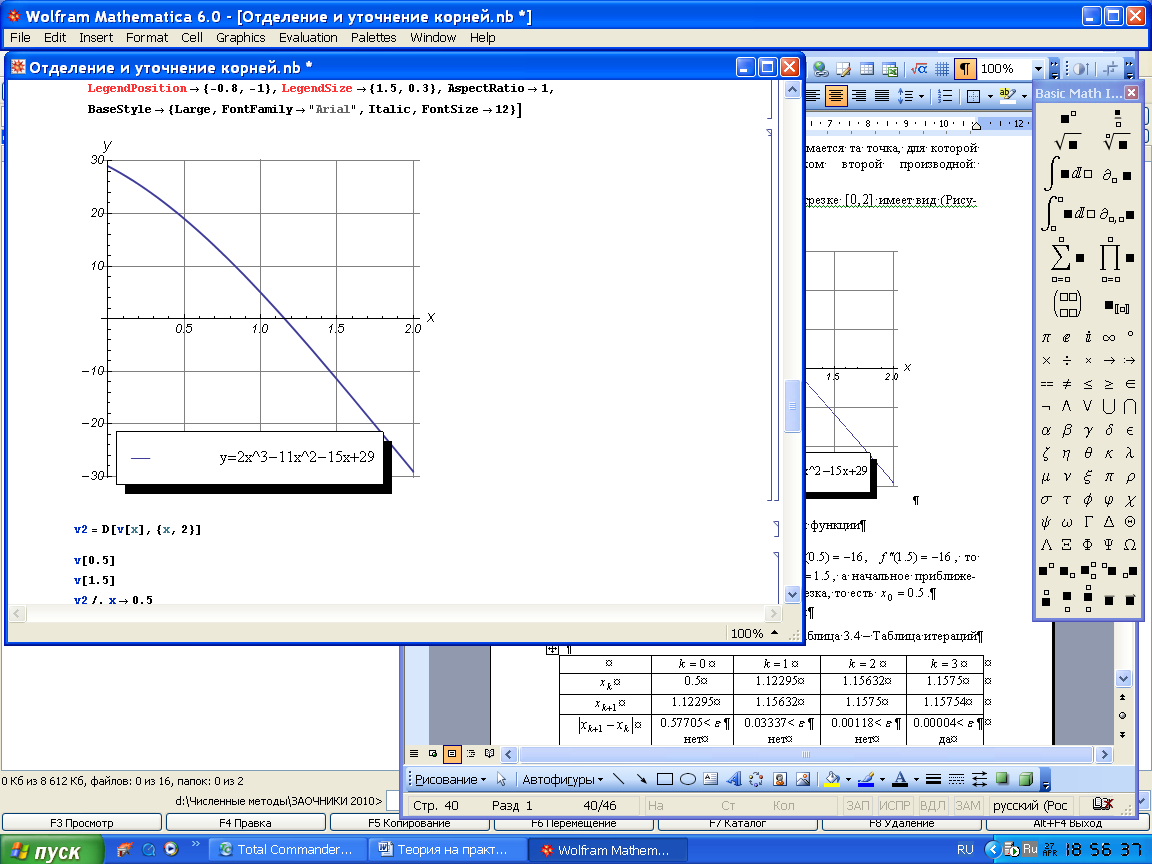
Рисунок 9.3 – График функции

Так как , то за неподвижный конец отрезка берем , а начальное приближение берем с противоположного конца отрезка, то есть .

Вычисления приведены в таблице 9.4.

Таблица 9.4 – Таблица итераций


0.5	1.12295	1.15632	1.1575
1.12295	1.15632	1.1575	1.15754
0.57705< нет	0.03337< нет	0.00118< нет	0.00004< да

Точность достигнута на четвертой итерации и за уточненный корень принимается значение (сравнить с методом итерации).

9.3.3 Метод Ньютона

Как и в пункте 9.3.1 уточним корень . В методе Ньютона последовательность приближений задается формулой:

. (9.13)

За неподвижный конец (начальное приближение) отрезка принимается та точка, для которой знак функции совпадает со знаком второй производной: . Исходя из результатов пункта 9.3.1, имеем . Значение первой производной определяется формулой