125 Кібербезпека / 4 Курс / 4.2_Управління інформаційною безпекою / Лiтература / V_P_Babak_A_A_Kliuchnykov-Teoreticheskye_osnovy_zashchity_informat

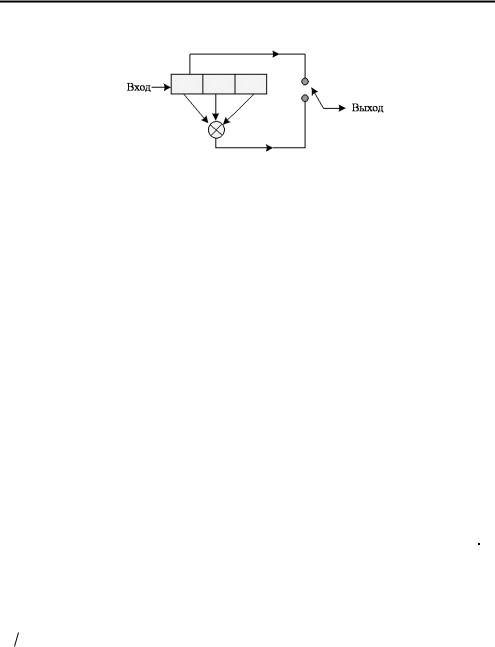
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЗАЩИТЫ ИНФОРМАЦИИ

даны длина кодового ограничения и степень кодирования, максимально возможное значение просвета снижается.

Рис. 7.38. Систематический сверточный кодер (степень кодирования 12 , K 3 )

Максимальный просвет в случае, если степень кодирования равна 12, для систематического и несистематического кодов при K , что изменяется от 2 до 8, приведен в табл. 7.15. При большой длине кодового ограничения результаты отличаются еще сильнее.

Катастрофическая ошибка возникает, когда конечное количество ошибок в кодовых символах вызывает бесконечное количество битовых ошибок в декодированных данных.

Месси (Massey) и Сейн (Sain) указали необходимые и достаточные условия для сверточного кода, при которых возможно распространение катастрофических ошибок. Условием распространения катастрофических ошибок для кода со степенью кодирования 12, реализованного на полиномиальных гене-

раторах, будет наличие у генераторов общего полиномиального множителя (степени, не меньшей единицы).

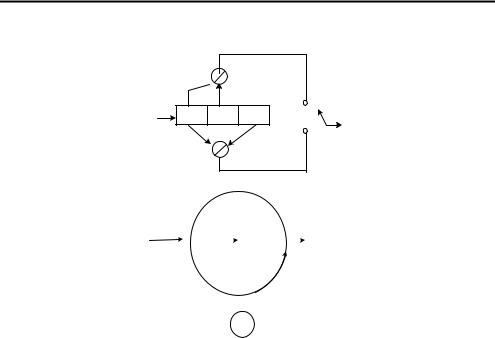
Например, на рис. 7.39, а изображен кодер K 3, степень кодирования

570

Глава 7. Кодирование информации

Итак, в кодере, показанном на рис. 7.39, а, может происходить накопле-

ние катастрофической ошибки.

00

б

Рис. 7.39. Кодер, в котором возможно накопление катастрофической ошибки: а - кодер; б - диаграмма состояния

Катастрофическая ошибка может появиться тогда и только тогда,

когда любая петля пути на диаграмме состояний кода произвольной степени кодирования имеет нулевой весовой коэффициент (нулевое расстояние к нулевому пути).

Пример 7.30. Чтобы проиллюстрировать это, рассмотрим пример, приведенный на рис. 7.39. На диаграмме (рис. 7.39, б) узел состояния a 00 разбит на два узла а и е, как и раньше. Предположим, что нулевой путь является правильным, тогда неправильный путь abdd...dce имеет точно 6 единиц независимо от того, сколько раз мы обойдем вокруг петли в узле d. Поэтому, например, для канала BSC к выбору этого неправильного пути могут привести три канальные ошибки. На таком пути может появиться значительно большее количество ошибок (две плюс количество раз обхода петли). Для кодов со степенью кодирования 1n можно увидеть, что когда каждый сум-

матор в кодере имеет парное количество соединений, петли, которые соответствуют информационным состояниям со всеми единицами, будут иметь нулевой вес, а соответственно, код будет катастрофическим.

Единственное преимущество описанного прежде систематического кода заключается в том, что он никогда не будет катастрофическим, поскольку каждая петля должна содержать, по крайней мере, одну ветку, порождаемую

571

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЗАЩИТЫ ИНФОРМАЦИИ

ненулевым входным битом. Итак, каждая петля должна содержать ненулевой кодовый символ. Тем не менее, можно показать, что только небольшая часть несистематических кодов (кроме того, в котором все сумматоры имеют парное количество соединений) является катастрофической.

Граница рабочих характеристик сверточных кодов. Можно показать,

что при когерентной модуляции в канале с адаптивным белым гауссовым шумом вероятность битовой ошибки

где Ec / N0 - отношение энергии канального символа к спектральной плотно-

Eb / N0 - отношение энергии информационного бита к спектральной плотности мощности шума). Итак, для кода со степенью кодирования 12 и просветом d f 5 в случае использования когерентной схемы BPSK и твердой схемы принятия решений при декодировании можем записать

стижения определенной вероятности появления ошибок в кодированной системе сравнительно с некодированной системой с той самой модуляцией и характеристиками канала.

Верхние границы эффективности кодирования приведены в табл. 7.16.

Они сравниваются с некодированным сигналом с когерентной модуляцией для нескольких значений минимальных просветов сверточного кода.

572

Глава 7. Кодирование информации

Длина кодового ограничения в гауссовом канале с твердой схемой принятия решений при декодировании изменяется от 3 до 9. В таблице отображен тот факт, что даже при использовании простого сверточного кода можно достичь значительной эффективности кодирования. Реальная эффективность кодирования будет изменяться в зависимости от необходимой вероятности появления битовых ошибок.

Оценки эффективности кодов, которые сравниваются с некодированным сигналом с когерентной модуляцией, реализованной аппаратным путем или путем моделирования на компьютере, в гауссовом канале с мягкой схемой принятия решений при декодировании приведены в табл. 7.17.

Таблица 7.17

Некодированное значение Eb / N0 представлено в крайнем левом столб-

це. Из табл. 7.17 можно видеть, что эффективность кодирования возрастает с уменьшением вероятности появления битовой ошибки. Однако эффективность кодирования не может возрастать бесконечно. Как вытекает из табл. 7.17, она имеет верхнюю границу. Эту границу (в децибелах) можно выразить как эффективность кодирования

где r - степень кодирования, a df - просвет.

Основные выводы

Форматирование источника сообщений - это процесс аналоговоцифрового преобразования информационного сигнала источника сообщения в цифровой сигнал с помощью дискретизации и квантования сигнала и его представления в двоичной системе исчисления.

Кодирование источника сообщений проводится с целью обеспечения компактного представления данных, сокращение объема информации, кото-

573

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЗАЩИТЫ ИНФОРМАЦИИ

рая вырабатывается источником, и для повышения скорости ее передачи или сокращения полосы частот.

Существуют два типа систем сжатия данных:

системы сжатия без потерь информации (неразрушительное сжатие); системы сжатия с потерями информации (разрушительное сжатие). Выбор системы неразрушительного или разрушительного сжатия зави-

сит от типа данных, которые подлежат сжатию.

Передача данных по каналам связи и их хранение всегда происходит при наличии помех. Поэтому принятое (воспроизведенное) сообщение всегда определенной мерой отличается от переданного, т.е. на практике невозможна абсолютно точная передача при наличии помех в канале связи (в системе хранения).

Источники данных имеют ограниченный динамический диапазон и вырабатывают начальные сообщения с определенным уровнем искажений и ошибок. Этот уровень может быть большим или меньшим, но абсолютной точности воспроизведения достичь невозможно.

Критерием качества кода относительно кодирования источника сообщения является средняя длина кодовых слов.

Арифметическое кодирование нуждается в большой (в пределе бесконечной) точности вычислений, которая приводит к недопустимо высокой сложной реализации.

Простым и широко используемым для сжатия изображений и звуковых сигналов методом неразрушительного кодирования является метод дифференциального кодирования и кодирование длины повторений.

Задача помехоустойчивого корректирующего кодирования - обеспечение целостности информационных объектов с применением помехоустойчивых корректирующих кодов.

Помехоустойчивым корректирующим кодированием называется такой вид кодирования, который дает возможность реализовать программные, аппаратные или программно-аппаратные средства выявления и устранение искажений в информационных сообщениях.

Сверточным кодированием называется алгоритм кодирования, согласно которому кодер зависит не только от информационных символов в данный момент, а и от предыдущих символов на его входе или выходе.

Оптимальным есть такой декодер, который работает по принципу максимального правдоподобия и минимизирует вероятность ошибки в информационном сообщении при условии, что все переданные последовательности равновероятные.

Сверточные (рекурентные, цепи) коды используются для кодирования непрерывной последовательности двоичных символов путем введения в эту последовательность специальных проверочных (избыточных) символов с целью выявления и исправление искажений в информационных сообщениях.

574

Глава 7. Кодирование информации

Вопросы для самоконтроля

1.Раскройте содержание разрушительного и неразрушительного сжатия информации.

2.В каком случае код является однозначно декодированным?

3.Раскройте понятие «префиксности кода».

4.Выведите необходимое и достаточное условия префиксности.

5.Определите алгоритм построения кодового дерева Хаффмана.

6.В чем заключается кодирование последовательностей сообщений?

7.Раскройте алгоритм декодирования арифметического кода.

8.Раскройте понятие «код с конечной памятью».

9.На какие группы можно поделить все словарные методы кодирова-

ния?

10.В каких случаях используется метод дифференциального кодирова-

ния?

11.Объясните основные способы (механизмы) обеспечения целостности (и в определенном значении - доступности) информации в условиях естественных действий.

12.Объясните особенности способов обеспечения целостности информационных объектов с применением помехоустойчивых корректирующих кодов.

13.Объясните принципы построения помехоустойчивых кодов.

14.Что такое относительная скорость и избыточность кода?

15.Объясните принципы построения двоичных кодов с проверкой на парность или непарность (контроль по модулю 2).

16.Объясните принцип построения кодов Хэмминга. Какие их возможности относительно обнаружения и исправления ошибок?

17.Объясните алгоритмы кодирования и декодирование с применением кодов Хэмминга.

18.Построение циклических кодов. Чем определяется их корректирующая способность?

19.Объясните алгоритмы кодирования и декодирования с применением циклических кодов.

20.Объясните принципы построения сверточных кодов. Какие их возможности относительно обнаружения и исправления искажений?

21.Объясните алгоритмы кодирования и декодирования с применением сверточных кодов.

22.Коды Рида - Соломона. Принципы построения и возможности.

575

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЗАЩИТЫ ИНФОРМАЦИИ

The main conclusions

Formatting of a source of messages is a process of analog-to-digital conversion of an information signal of a source of messages in a digital signal by means of digitization and quantization of a signal and its representation in binary system of calculation.

The coding of a source of messages is conducted with the purpose of support of compact data representation, reduction of information volume that is made by a source and for rise of its transfer rate or reduction of a band.

There are two types of systems of data compression: systems of compression without losses of the information (nondestructive compression); systems of compression with losses of the information (destructive compression).

The choice of system of nondestructive or destructive compression depends on a type of data which are subjected to compression.

The transmission of data on communication channels and their storage are always conducted at presence of interferences of different type. Therefore the accepted (reproduced) message always differs from transferred to certain extent, that is in practice absolutely exact transmission at presence of interferences in a communication channel(in system of storage) is impossible.

The optimal decoder is a decoder that works on a principle of maximal plausibility and it minimizes probability of an error in an information message on condition that all transmitted sequences are equally possible.

Folding (recurrent, chain) codes are used for the coding of continuous sequence of binary symbols by bringing of special checking (redundant) symbols in this sequence with the purpose of revealing and correction of distortions in information messages.

Ключевые слова

576

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЗАЩИТЫ ИНФОРМАЦИИ

8.1. Модели и системы шифрования

Желание общаться конфиденциально было присущим человеку издавна. История секретного общения богата уникальными изобретениями, часть из которых мы рассмотрим дальше. Термины шифрование и кодирование означают преобразование сообщений, которые выполняются передатчиком, а термины дешифрации и декодирования — соответствующие обратные преобразования, которые осуществляются получателем информации.

Греческое слово «криптография» происходит от слов «kryptos» (тайный,

спрятанный) и «graphy» (запись) и охватывает разработку методов и средств обеспечения безопасности передачи информационных сообщений.

Зарождение криптографии началось в глубокой давности, из которой до нас дошло немало систем шифрования, скорее всего появившихся одновременно с письменностью в IV тысячелетии до н.э. Методы секретного переписывания были независимо найдены во многих древних обществах (Египет, Шумер, Китай). По свидетельству Геродота, в Древнем Египте роль шифра как правило выполнял специально созданный жрецами язык, в котором параллельно существовали три алфавита: письменный, священный и таинственный (последний применялся пророками для скрытия содержания сообщений).

С распространением письменности криптография стала формироваться как самостоятельная наука. Первые криптосистемы появляются уже в начале нашей эры. Так, Цезарь в своей переписке использовал систематический шифр, которому было присвоено его имя.

Разработка и внедрение методов и средств безопасности передачи информационных сообщений на основе криптографических преобразований является задачей криптографов. Криптоаналитики нарушают эту безопасность, используя криптоанализ, соориентированный на взлом шифротекстов (шифров), которые представляют собой данные, поданные в зашифрованной форме (со скрытым семантическим содержанием), то есть образованные после шифрования (криптографического преобразования) открытого текста (с нескрываемым семантическим содержанием).

До появления информационных технологий криптография состояла из алгоритмов на символьной основе. Разные криптографические алгоритмы либо заменяли одни символы другими, либо переставляли символы.

Стремительное развитие криптографические системы приобрели в годы первой и второй мировых войн. Появление вычислительных средств в 1950-х годах ускорило разработку и усовершенствование методов шифрования.

Современная криптография базируется на последних достижениях математики, ряда фундаментальных физических и инженерных дисциплин в сочетании с новейшими информационными технологиями.

578

Глава 8. Шифрование и дешифрование информации

Основными направлениями использования криптографических методов стали передача конфиденциальной информации в каналах связи, установление подлинности переданных сообщений, хранение информации (документов, баз данных) на носителях в зашифрованном (закрытом) виде.

Появление новых мощных вычислительных систем, новейших сетевых технологий и нейронных моделей постоянно побуждает к созданию новых криптосистем и внедрению тщательного анализа и совершенствованию уже известных методов.

В основу каждой закрытой информационной системы положено использование алгоритмов шифрования как основного средства сохранения конфи-

математической функции с целью обеспечения конфиденциальности, то есть предотвращение исключения полезной информации из канала передачи данных несанкционированным пользователем (рис. 8.1).

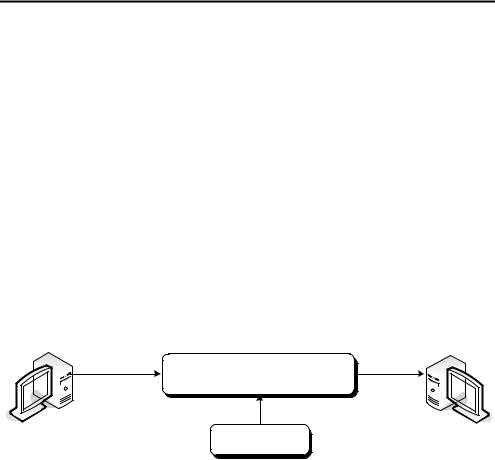
Криптографическая система

Рис. 8.1. Структурная схема процесса шифрования

Криптографическим алгоритмом называют алгоритм или математическую функцию, которая используется для шифрования и расшифровывания открытого текста из алфавита сообщения A{ i

Алфавит сообщения A{ i (i 1, 2, , K) - конечное множественное

число знаков, используемых для шифрования информации.

Текст (открыт текст) - упорядоченный набор знаков M из элементов алфавита A{ i , который содержит полезную информацию.

Под шифровкой в широком смысле понимают процесс преобразования исходного текста, который называют также открытым текстом, в шифрованный текст.

Расшифровывание - процесс, обратный шифрованию, то есть восстановление открытого текста из алфавита сообщения A{ i (i 1, 2, , K ) на основе определенного ключа (алгоритма или обратной математиче

579