
125 Кібербезпека / 5 Курс / 5.1_Оптимізаційні методи та моделі / Література / Математичне програмування Навч.-мет
...pdfC = (c1, c2, …, cn) – вектор коефіцієнтів при змінних у цільовій функції. Загальна задача лінійного програмування (1) – (3) геометрично
інтерпретується так: кожне і-те обмеження, що має вигляд рівняння
ai1x1 + ai2x2 + … + ainxn = bi,
в n-вимірному просторі основних змінних x1, x2, …, xn задає гіперплощину. Кожному обмеженню вигляду (2) і (3) відповідають гіперплощина та півпростір, який лежить по один бік від цієї гіперплощини. У перетині всіх півпросторів, що визначаються обмеженнями задачі (2) і (3), утворюється опуклий багатогранник її допустимих розв’язків.
Цільову функцію
Z= c1x1 + c2x2 + … + cnxn
вn-вимірному просторі основних змінних можна геометрично
інтерпретувати як сім’ю паралельних гіперплощин, положення кожної з яких визначається значеннями параметра Z.
Завдання для самостійної роботи Задача 1. Підприємство виготовляє продукцію чотирьох видів і для
цього використовує ресурси 1, 2, 3. Норми витрат цих ресурсів на одиницю продукції, запаси ресурсів та ціну кожного виду продукції наведено в таблиці.
|
Норма витрат на одиницю |
Запас |
|||||
Ресурс |
|
продукції за видами |
|
||||
|
|
ресурсу |
|||||
|
A |
|
B |
C |
|
D |
|
|
|
|
|
||||
1 |
2 |
|
1 |
1 |
|
3 |
300 |
2 |
1 |
|
– |
2 |
|
1 |
70 |
3 |
1 |
|
2 |
1 |
|
– |
340 |
Ціна продукції |
8 |
|
3 |
2 |
|
1 |
|
Сформулювати економіко-математичну модель задачі.
Задача 2. Фірма виготовляє деякий препарат побутової хімії. Продукція фірми, що надходить на споживчий ринок, має відповідати певним вимогам, які характеризуються трьома показниками: очищувальні й дезинфікувальні властивості, а також подразнювальний вплив на шкіру людини. Кожний із цих показників вимірюється за лінійною шкалою від 0 до 100 од. Кінцевий продукт виробництва утворюється як суміш основних компонентів A, B, C, характеристики яких наведено в таблиці, і повинні мати не менше ніж 60 од. очищувальних властивостей і принаймні 60 од. дезинфікувальних.
11
Компонент |
Очищувальні |
Дезинфікувальні |
Подразнювальний |
|
властивості |
властивості |
вплив на шкіру |
A |
90 |
30 |
70 |
B |
65 |
85 |
50 |
C |
45 |
70 |
10 |
Сформулювати економіко-математичну модель задачі.
Задача 3. Підприємство випускає r видів хімічної продукції в обсягах D1, D2, … Dr одиниць, кожна з яких є сумішшю кількох компонентів. Припустимо, що таких компонентів є n і запаси вихідної сировини відповідно дорівнюють A1, A2, …, An одиниць. Необхідно так виготовити суміші, щоб прибуток від реалізації продукції був найбільшим. Скласти математичну модель задачі.
Задача 4. Грошові кошти фірми можуть використовуватися для фінансування двох проектів. Проект А гарантує отримання через рік прибутку в розмірі 60 центів на кожний вкладений долар. Проект В гарантує отримання прибутку в розмірі 2 дол. на кожний інвестований долар, але через два роки. При фінансуванні проекту В період інвестиції має бути кратним двом рокам. Визначити, як потрібно розпорядитися капіталом у сумі 100000 дол., щоб максимізувати загальний прибуток, який можна отримати через три роки після початку інвестицій. Скласти математичну модель задачі.
Задача 5. На трьох складах (І, ІІ, ІІІ) знаходиться відповідно 90, 70, 50 тонн борошна, яке необхідно перевезти в магазини (1, 2, 3, 4) відповідно в кількості 80, 60, 40, 30 тонн. Вартість перевезення 1 тонни борошна в магазини 1, 2, 3, 4 зі складу І дорівнює відповідно 2, 1, 3, 2 гривні, зі складу ІІ – 2, 3, 3, 1 гривня, зі складу
ІІІ – 3, 3, 2, 5 гривень. Скласти економіко-математичну модель задачі.
12

Тема 2. Графічний метод розв’язання задач лінійного програмування
Для розв’язання двовимірних задач лінійного програмування, тобто задач із двома змінними, а також деяких тривимірних задач застосовують графічний метод, що грунтується на геометричній інтерпретації та аналітичних властивостях задач лінійного
програмування. |
|
|
Розглянемо таку задачу. |
|
|
Знайти екстремум (мінімум, максимум) функції |
|
|
Z = c1x1 + c2x2 max(min). |
(1) |
|
за умов |
|
|
a11x1 + a12x2 { , =, } b1, |
|
|
a21x1 + a22x2 { , =, } b2, |
|
|
……………………………………., |
(2) |
|
am1x1 + am2x2 { , =, } bm, |
|
|
x1 0, x2 |
0. |
(3) |
Припустимо, що система (2) за умов (3) сумісна та область її |
||
допустимих розв’язків непорожня. |
|
|
Згідно з |
геометричною інтерпретацією задачі |
лінійного |
програмування, кожне i-те обмеження-нерівність (2) визначає півплощину з граничною прямою ai1x1 + ai2x2 = bi (i = 1, 2, …, m). Системою обмежень (2) описується спільна частина або переріз усіх зазначених півплощин, тобто множина точок, координати яких задовольняють усі обмеження задачі. Таку множину точок називають багатокутником розв’язків, або областю допустимих планів (розв’язків) задачі лінійного програмування.
Умова (3) невід’ємності змінних означає, що область допустимих розв’язків задачі належить першому квадранту системи координат двовимірного простору. Цільова функція задачі лінійного програмування геометрично інтерпретується як сім’я паралельних
прямих c1x1 + c2x2 = const.
Якщо задача лінійного програмування має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин багатокутника розв’язків. А якщо цільова функція досягає екстремального значення більш як в одній вершині багатокутника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією цих вершин.
Отже, розв’язати задачу лінійного програмування графічно означає знайти таку вершину багатокутника розв’язків, у результаті
13

підстановки координат якої в (1) лінійна цільова функція набуває найбільшого (найменшого) значення.
Алгоритм графічного методу розв’язування задачі лінійного програмування складається з розглянутих нижче кроків.
1.Будуємо прямі лінії, рівняння яких дістаємо заміною в обмеженнях задачі (2) знаків нерівностей на знаки рівностей.
2.Визначаємо півплощини, що відповідають кожному обмеженню задачі.
3.Знаходимо багатокутник розв’язків задачі лінійного програмування.
4.Будуємо вектор N = {c1, c2}, що задає напрям зростання значень цільової функції задачі.
5.Будуємо пряму c1x1 + c2x2 = const, перпендикулярну до вектора N .
6.Переміщаючи пряму c1x1 + c2x2 = const в напрямі вектора N (для задачі максимізації) або в протилежному напрямі (для задачі мінімізації), знаходимо вершину багатокутника розв’язків, де цільова функція досягає екстремального значення.
7.Визначаємо координати точки, в якій цільова функція набуває максимального (мінімального) значення, і обчислюємо екстремальне значення цільової функції в цій точці.
Уразі застосування графічного методу для розв’язування задач лінійного програмування можливі такі випадки:
1) цільова функція набуває максимального значення в єдиній вершині багатокутника розв’язків;
2) екстремального значення цільова функція досягає в будь-якій точці відрізка. Тоді задача лінійного програмування має альтернативні оптимальні плани;
3) задача лінійного програмування не має оптимальних планів, коли цільова функція не обмежена зверху (знизу) або система обмежень несумісна.
Задача. Фірма спеціалізується на виробництві офісних меблів, зокрема вона випускає дві моделі збірних книжкових полиць А та В. Полиці обох моделей обробляються на верстатах 1 і 2. Тривалість обробки (у хвилинах) однієї полиці моделі А на верстатах 1 і 2 – 30 і 12 хв., а моделі В відповідно 15 і 26 хв. Час роботи верстатів 1 і 2 становить відповідно 40 і 36 год. на тиждень. Прибуток фірми від реалізації однієї полиці моделі А дорівнює 50 у.о., а моделі В – 30 у.о. Вивчення ринку збуту показало, що тижневий попит на полиці моделі А ніколи не перевищує попиту на моделі В більше як на 30 одиниць, а попит на полиці моделі В не перевищує 80 одиниць на тиждень.
14

Визначити обсяги виробництва книжкових полиць різних моделей, що максимізують прибуток фірми. Побудувати економікоматематичну модель задачі та розв’язати її графічно.
Побудова математичної моделі. Нехай x1 – кількість полиць моделі А, що виготовляється фірмою за тиждень, а x2 – відповідна кількість полиць моделі В. Цільова функція моделі – максимізація прибутку фірми від реалізації продукції. Математично вона записується так:
Z = 50x1 + 30x2 max.
Обмеження математичної моделі враховують час роботи верстатів 1 і 2 для обробки продукції та попит на полиці різних моделей.
Обмеження на час роботи верстатів 1 і 2 набирають такого вигляду: для верстата 1
30x1 + 15x2 |
2400 (хв.); |
|||
для верстата 2 |
|
|
||
12x1 |
+ 26x2 |
2160 (хв.). |
||
Обмеження на попит набирають вигляду: |
||||
x1 – x2 |
30 і |
x2 |
80. |
|
Отже, економіко-математична модель поставленої задачі має |
||||
вигляд |
|
|
|
|
Z = 50x1 + 30x2 |
max, |
|||
30x1 |
+ 15x2 |
2400, |
||
12x1 |
+ 26x2 |
2160, |
||
x1 – x2 |
30, |
|
|
|
x2 80.
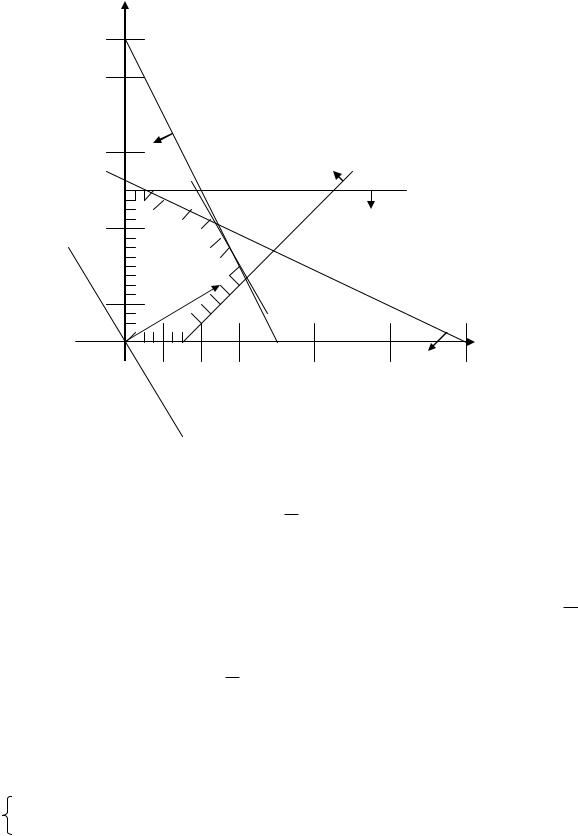
Розв’язання. Замінимо знаки нерівностей на знаки рівностей і побудуємо графіки відповідних прямих (рис.1). Кожна з побудованих прямих поділяє площину системи координат на дві півплощини. Координати точок однієї задовольняють розглянуту нерівність, а іншої
– не задовольняють. Щоб визначити необхідну півплощину (на рис. 1 її напрям позначено стрілкою), потрібно взяти будь-яку точку та перевірити, чи задовольняють її координати зазначене обмеження. Якщо задовольняють, то півплощина, в якій міститься вибрана точка, є геометричним зображенням нерівності. У протилежному випадку таким зображенням є інша півплощина. Умова невід’ємності змінних x1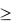 0, x2
0, x2  0 обмежує область допустимих планів задачі першим квадрантом системи координат. Переріз усіх півплощин визначає область допустимих планів задачі – шестикутник OABCDE.
0 обмежує область допустимих планів задачі першим квадрантом системи координат. Переріз усіх півплощин визначає область допустимих планів задачі – шестикутник OABCDE.
15
x2
160
100 |
|
|
|
|
B |
|
|
A |
|
|
|
60 |
|
C |
|
|
|
|
|
|
|
D |
Zmax |
O |
|
|
|
0 |
E |
|
x1 |
|
60 |
100 |
|
|
|
Z=0 |
Рис. 1 |
|
Поставлену задачу буде розв’язано, якщо ми відшукаємо таку вершину багатокутника OABCDE, в якій цільова функція Z набуває найбільшого значення.
Для цього будуємо вектор N = {50; 30}. Він задає напрям збільшення значень цільової функції Z, а вектор, протилежний йому, – напрям їх зменшення.
Побудуємо лінію, що відповідає, наприклад, значенню Z = 0. Це буде пряма 50x1 + 30x2 = 0, яка перпендикулярна до вектора N і проходить через початок координат. Оскільки маємо визначити найбільше значення цільової функції, то пересуваємо пряму 50x1 + 30x2 = 0 в напрямі вектора N доти, доки не визначимо вершину багатокутника, яка відповідає оптимальному плану задачі. Останньою спільною точкою цієї прямої та багатокутника OABCDE є точка C. Координати цієї точки визначають оптимальний план задачі.
Координати точки С визначаються перетином прямих
30x1 + 15x2 = 2400,
12x1 + 26x2 = 2160.
Розв’язавши цю систему, дістанемо x1 = 50, x2 = 60. Отже, X = (50; 60); max Z = 50  50 + 30
50 + 30  60 = 4300.
60 = 4300.
16
Це означає, що коли фірма щотижня виготовлятиме 50 збірних книжкових полиць моделі А та 60 – моделі В, то вона отримає максимальний прибуток в 4300 у.о. При цьому тижневий фонд роботи верстатів 1 і 2 буде використано повністю.
Приклади та завдання для самостійної роботи Задача 1. Комерційна фірма рекламує свою продукцію,
використовуючи місцеві радіота телевізійну мережі. Витрати на рекламу в бюджеті фірми становлять 10000 дол. на місяць. Хвилина радіореклами коштує фірмі 5 дол., а телереклами – 90 дол. Фірма має намір використовувати радіорекламу принаймні вдвічі частіше, ніж рекламу на телебаченні. Досвід показав: обсяг збуту, що його забезпечує 1 хв. телереклами, у 30 разів перевищує обсяг збуту, що його забезпечує 1 хв. радіореклами. Визначити оптимальний розподіл коштів, які щомісяця мають витрачатися на рекламу, за якого обсяг збуту продукції фірми буде найбільшим.
Задача 2. Підприємство виготовляє письмові столи типів А і В. Для одного столу типу А необхідно 2 м2 деревини, а для столу типу В – 3 м2. Підприємство може отримати до 1200 м2 деревини за тиждень. Для виготовлення одного столу типу А потрібно 12 хв. роботи обладнання, а для моделі В – 30 хв. Обладнання може використовуватися 80 год. на тиждень. Відомо, що за тиждень може бути реалізовано до 550 столів. Відомо також, що прибуток від реалізації одного письмового столу типу А становить 30 дол., а типу В – 40 дол. Скільки столів кожного типу необхідно виготовляти за тиждень?
Задача 3. Підприємство електронної промисловості виготовляє дві моделі радіоприймачів, причому кожна модель складається на окремій технологічній лінії. Добовий обсяг виробництва першої лінії становить 60, а другої – 70 од. На один радіоприймач першої моделі витрачається 10 однотипних елементів електронних схем, а на радіоприймач другої моделі – 8. Максимальний добовий запас елементів, що використовуються у виробництві, становить 1000 од. Прибуток від реалізації одного радіоприймача першої та другої моделі дорівнює відповідно 35 та 25 дол. Визначити оптимальні обсяги виробництва радіоприймачів обох моделей. Записати економіко-математичну модель задачі та розв’язати її графічно.
Графічним методом визначити оптимальні плани задач лінійного програмування
17
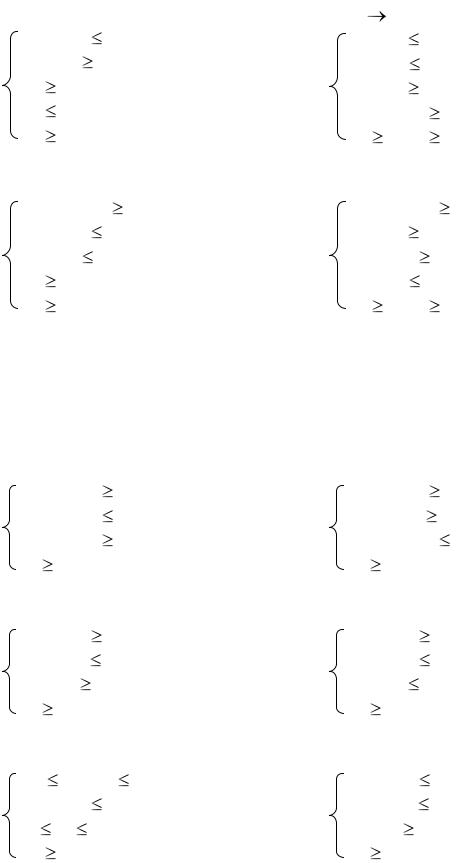
Задача 4. |
Задача 5. |
||||
min(max)(x1 + 2x2); |
x1 – 2x2 |
min; |
|||
x1 + 2x2 |
10, |
x1 |
– x2 |
1, |
|
x1 + x2 |
1, |
x1 + x2 |
2, |
||
x2 |
1, |
|
x1 |
– x2 |
0, |
x2 |
4, |
|
2x1 + 2x2 1, |
||
x1 |
0. |
|
x1 |
0, x2 |
0. |
Задача 6. |
|
Задача 7. |
|||
min(max)(x1 + 3x2); |
min(max)(x1 – 3x2); |
||||
10x1 + 3x2 |
30, |
10x1 + 3x2 30 |
|||
–x1 + x2 |
5, |
x1 – x2 |
4, |
||
x1 |
+ x2 10, |
–x1 + x2 |
3, |
||
x1 |
0, |
|
x1 |
+ x2 |
10, |
x2 |
0. |
|
x1 |
0, x2 |
0. |
Завдання для контрольних робіт
Розв’язати |
|
графічним |
методом |
такі |
задачі |
лінійного |
|||
програмування. |
|
|
|
|
|
|
|
|
|
Задача 1. |
|
Задача 2. |
|
|
|||||
min(-2x1 + 5x2); |
|
max(3x1 – 2x2); |
|
|
|||||
7x1 + 2x2 |
14, |
|
7x1 + 2x2 |
14, |
|
||||
5x1 + 6x2 |
30, |
|
-x1 + 2x2 |
2, |
|
||||
3x1 + 8x2 |
24, |
|
7x1 + 10x2 |
28, |
|||||
xj |
0, j = 1, 2. |
|
xj |
0, j = 1, 2. |
|
||||
Задача 3. |
|
Задача 4. |
|
|
|||||
min(x1 + 2x2); |
|
|
|
min(x1 – x2); |
|
|
|
||
3x1 + x2 |
|
3, |
|
3x1 + x2 |
|
3, |
|
||
3x1 – x2 |
|
0, |
|
3x1 + x2 |
|
6, |
|
||
x1 – x2 |
3, |
|
x1 – x2 |
3, |
|
||||
xj |
0, j = 1, 2. |
|
xj |
0, j = 1, 2. |
|
||||
Задача 5. |
|
Задача 6. |
|
|
|||||
max(x1 + x2); |
|
|
|
max(x1 + x2); |
|
|
|
||
-2 x1 – x2 2, |
|
x1 + 2x2 |
|
1, |
|
||||
x1 + 3x2 |
|
1, |
|
x1 – 3x2 |
1, |
|
|||
0 |
x1 |
5, |
|
x1 –x2 |
2, |
|
|
||
x2 |
0. |
|
|
|
xj |
0, j = 1, 2. |
|
||
18
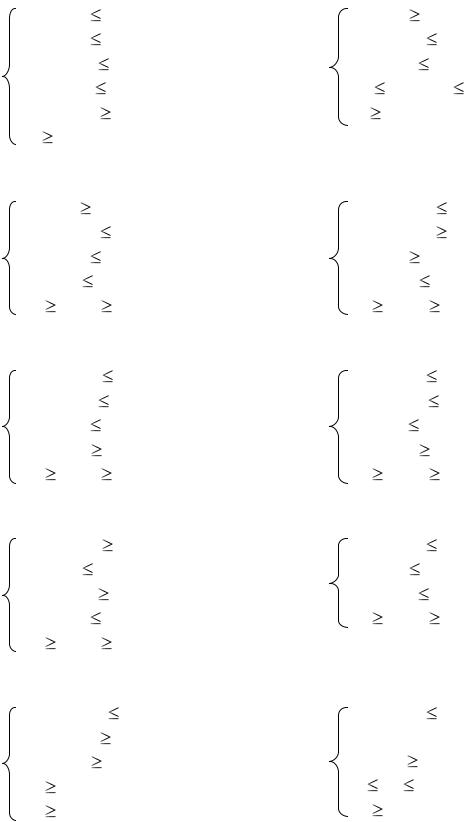
Задача 7.
max(2x1 + x2); |
|
||
x1 – 2x2 |
1, |
||
2x1 |
– x2 |
1, |
|
-3x1 + x2 |
0, |
||
2x1 |
– x2 |
0, |
|
2x1 |
– 3x2 |
3, |
|
xj |
|
0, j = 1, 2. |
|
Задача 9. |
|||
max(-3x1 + 2x2); |
|||
x1 – x2 |
0, |
||
3x1 |
– 2x2 |
6, |
|
x1 |
– 4x2 |
0, |
|
x1 |
+ x2 |
6, |
|
x1 |
|
0, x2 |
0. |
Задача 11. min(max)(2x1 – x2);
3x1 + 2x2 |
12, |
|
-2x1 + x2 |
4, |
|
x1 |
– 3x2 |
0, |
x1 |
+ 2x2 |
2, |
x1 |
0, x2 |
0. |
Задача 13. |
||
min(max)(-x1 + x2);
5x1 + 2x2 |
10, |
|
x1 + x2 4, |
||
-4x1 + x2 |
-8, |
|
x1 – 2x2 |
0, |
|
x1 |
0, x2 |
0. |
Задача 15. |
||
max(x1 + x2); |
|
|
-2x1 + 4x2 |
8, |
|
3x1 – 2x2 |
0, |
|
x1 |
+ 3x2 |
3, |
x1 |
1, |
|
x2 |
0. |
|
Задача 8. |
|
|||
max(3x1 + 4x2); |
|
|||
x1 + x2 |
|
-1, |
|
|
-x1 + 2x2 |
2, |
|||
2x1 – x2 |
|
2, |
|
|
-1 |
-x1 + x2 |
1, |
||
xj |
0, j = 1, 2. |
|||
Задача 10. |
|
|||
min(max)(2x1 – 3x2); |
||||
-5x1 + 3x2 |
15, |
|||
-2x1 + 3x2 |
0, |
|||
x1 + x2 |
|
2, |
|
|
2x1 + x2 |
|
10, |
||
x1 |
0, x2 |
0. |
||
Задача 12. |
|
|||
min(max)(5x1 – 2x2); |
||||
-x1 + 2x2 |
5, |
|||
5x1 – 2x2 |
10, |
|||
x1 – x2 |
|
1, |
|
|
2x1 + x2 |
|
2, |
|
|
x1 |
0, x2 |
0. |
||
Задача 14. |
|
|||
min(max)(-2x1 + x2); |
||||
-3x1 + x2 |
1, |
|||
x1 + x2 |
|
2, |
|
|
x1 – 2x2 |
|
0, |
|
|
x1 |
0, x2 |
0. |
||
Задача 16. |
|
|||
min(2x1 – 10x2); |
|
|||
-x1 + 5x2 |
5, |
|||
x1 + x2 = 6, |
|
|||
x1 – x2 |
0, |
|
||
0 |
x1 |
5, |
|
|
x2 |
0. |
|
|
|
19
Задача 17. |
|
||
min(2x1 – 4x2); |
|
||
3x1 – 4x2 |
|
24, |
|
-3x1 – 8x2 |
-48, |
||
x1 – x2 |
5, |
|
|
x1 |
4, |
|
|
x2 |
0. |
|
|
Задача 19. |
|
||
min(2x1 – x2); |
|
|
|
4x1 + 3x2 |
9, |
||
x1 – x2 |
3, |
|
|
-4x1 + 6x2 |
12, |
||
-3x1 |
– 2x2 |
-4. |
|
Задача 21. |
|
||
min(x1 – x2); |
|
|
|
x1 + x2 |
1, |
|
|
x1 – 2x2 |
1, |
||
2x1 + 3x2 |
2, |
||
3x1 |
+ 2x2 |
3, |
|
x1 + x2 |
1/2, |
||
xj |
0, j = 1, 2. |
||
Задача 23. |
|
||
max(x1 + 3x2); |
|
|
|
-2x1 + x2 |
0, |
||
x1 + 2x2 |
10, |
||
x1 + x2 |
3, |
|
|
x1 – 2x2 |
5, |
||
0 |
x1 |
6, |
|
x2 |
0. |
|
|
Задача 25. |
|
||
min(max)(-3x1 + x2); |
|||
x1 + x2 |
1, |
|
|
x1 – x2 |
1, |
|
|
2x1 + x2 |
4, |
||
2x1 |
+ 2x2 |
6, |
|
x1 |
0, x2 |
|
0. |
Задача 18. |
|
||
max(-4x1 + 2x2); |
|
||
x1 – x2 |
5, |
|
|
4x1 + x2 |
3, |
||
-2x1 + x2 |
6, |
||
3x1 + 2x2 |
12. |
||
Задача 20. |
|
||
max(2x1 + 4x2); |
|
||
3x1 – 4x2 |
|
-12, |
|
x1 + x2 |
5, |
|
|
x1 |
4, x2 |
|
2, |
xj |
0, j = 1, 2. |
||
Задача 22. |
|
||
max(x1 + x2); |
|
|
|
x1 + 2x2 |
1, |
||
2x1 + x2 |
1, |
||
x1 – x2 |
1, |
|
|
x1 – 2x2 |
1, |
||
2x1 – x2 |
1, |
||
x1 |
0, x2 |
|
0. |
Задача 24. |
|
||
max(x1 + 2x2); |
|
|
|
x1 + 4x2 |
8, |
||
x1 – 2x2 |
6, |
||
3x1 – 2x2 |
|
-6, |
|
x1 + 2x2 |
12, |
||
x1 + x2 |
8, |
|
|
x1 |
0, x2 |
|
0. |
Задача 26. |
|
||
max(3x1 + 2x2); |
|
||
-x1 + 2x2 |
4, |
||
3x1 + 2x2 |
14, |
||
x1 – x2 |
3, |
|
|
x1 |
0, x2 |
|
0. |
20
