
- •Принцип однозначности:
- •Принцип предметности:
- •Принцип взаимозаменяемости:
- •Формула.
- •Правила приписывания значений термам
- •Терместь предметная константа k. - значение предметной константы k в модели m совпадает с результатом приписывания этой константе интерпретации.
- •Сложный терм вида - значение сложного терма равно результату применения функции к объектам из универсума.
- •Правила приписывания значений формулам
- •Для пропозициональных связок приписывание, так же как и в логике высказываний
Терместь предметная константа k. - значение предметной константы k в модели m совпадает с результатом приписывания этой константе интерпретации.
терм есть предметная переменная α.
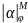 =φ(α)
– значение предметной переменной
совпадает с результатом приписывания
ϕ.
=φ(α)
– значение предметной переменной
совпадает с результатом приписывания
ϕ.Сложный терм вида - значение сложного терма равно результату применения функции к объектам из универсума.
7.Классическая логика предикатов: правила приписываний значений формулам, понятия общезначимой и выполнимой формул, определение основных логических отношений между формулами.
Правила приписывания значений формулам



Для пропозициональных связок приписывание, так же как и в логике высказываний
Для кванторов возможны 2 случая:
Первый – когда рассматриваемый нами универсум конечен. Тогда

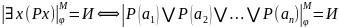
Если
универсум бесконечен - мы будем приписывать
условие истины для формул с кванторами,
задаем приписывание. Дано
 αA,
αA,
 Зафиксируем
некоторое исходное приписывание ϕ -
ǀ
Зафиксируем
некоторое исходное приписывание ϕ -
ǀ ǀϕ,
ǀ
ǀϕ,
ǀ ǀϕ.
Рассмотрим приписывания ψ1
и ψn(«пси
один и пси энное»), которые отличаются
от базового приписывания не более чем
значением переменной α. И пусть ϕ(α)=U0,
ϕ(
ǀϕ.
Рассмотрим приписывания ψ1
и ψn(«пси
один и пси энное»), которые отличаются
от базового приписывания не более чем
значением переменной α. И пусть ϕ(α)=U0,
ϕ( 1)=U1,….ϕ(
n)=Un
1)=U1,….ϕ(
n)=Un
ψ1(α)=V, ψ1( 1)=U1,….ψ1( n)=Un, где V – есть объект U0, либо другой объект из Универсума.
Значение
формулы
![]() α
А равно И, если значение ЛЮБОЙ
функции ψ, отличающейся от ϕ не
более, чем приписыванием значения
переменной α, равно И
α
А равно И, если значение ЛЮБОЙ
функции ψ, отличающейся от ϕ не
более, чем приписыванием значения
переменной α, равно И
| α А|ϕm = И ↔ ˚ψ (|A|ψ = И)
ψ α
ϕ
α
ϕ
|
α А|ϕm
= Л ↔
![]() ˚ψ
(|A|ψ = Л)
˚ψ
(|A|ψ = Л)
ψ α ϕ
| α А|ϕm = И ↔ ˚ψ (|A|ψ = И)
ψ α ϕ
| α А|ϕm = Л ↔ ˚ψ (|A|ψ = Л)
ψ α ϕ
(α пишется под знаком равенства)
Правила для формул с пропозициональными связками:
|![]() А|ϕ
m = И ↔
|А|ϕ m
= Л
А|ϕ
m = И ↔
|А|ϕ m
= Л
| А|ϕ m = Л ↔ |А|ϕ m = И
|А & В|ϕ m = И ↔ |А|ϕ m = И &˚ |В|ϕ m =И
|А & В|ϕ
m = Л ↔
|А|ϕm
= Л
![]() ˚
|В|ϕ m
=Л
˚
|В|ϕ m
=Л
|А В|ϕm = И ↔ |А|ϕm = И ˚ |В|ϕm=И
|А В|ϕm = Л ↔ |А|ϕm = Л &˚ |В|ϕm=Л
|А
![]() В|ϕm
= И ↔ |А|ϕm
= Л
˚
|В|ϕm=И
В|ϕm
= И ↔ |А|ϕm
= Л
˚
|В|ϕm=И
|А В|mϕ = Л ↔ |А|ϕm = И &˚ |В|ϕm=Л
Виды формул:
Формула А
является законом логики предикатов(общезначимой
формулой)если и только если А принимает
значение истина в каждой возможной
модели(реализации) М и при каждом
приписывании значений предметным
переменным ϕ(фи), т.е
 М
ϕǀАǀϕм=и
М
ϕǀАǀϕм=и
Формула
выполнима, если существует такая модель
и существует такое приписывание, в
котором формула принимает значение
истина, т.е
 М
ϕǀАǀϕм=и
М
ϕǀАǀϕм=и
Невыполнимая формула – это формула, принимающая значение Л во всех моделях и при любых приписываемых значениях предметным переменным, т.е М ϕǀАǀϕМ=л
Формула опровержима если и только если существует модель и существует приписывание, при которых формула принимает значение ложь, т.е М ϕǀАǀϕМ=Л
Отношения между формулами
Совместимость по истинности-существует такая модель и существует такое приписывание при которых каждая формула из Г(гамма) принимает значение истина.
совместимость
по истинности формул А и В -
 ϕ(ǀАǀϕМ=и
ϕ(ǀАǀϕМ=и
 ǀВǀϕМ=и)
ǀВǀϕМ=и)
Совместимость по ложности
Формулы из Г совместимы по ложности в том случае, если существует такая модель и такое приписывание значений переменным, при котором каждая формула из Г примет значение Л.
Логическое следование.
Из множества посылок Г (гамма) логически следует формула В, если и только если в любой модели и при любом приписывании, при котором все посылки из Г истинны, формула В тоже будет истинна(не существует такой модели и такого приписывания, при котором каждая формула из Г принимает значение истина, а формула В – значение ложь).
Формулы взаимовыражения:
 A
A ¬
¬ ¬A
¬A
 ¬
¬A
¬
¬A
8. Классическая логика предикатов: понятия свободного и связанного вхождения переменной в терм и в формулу, замкнутые термы и формулы. Понятие правильной подстановки.
Область
действия квантора в формулах
 .
Формула А – область действия квантора
по α переменной.
.
Формула А – область действия квантора
по α переменной.
Вхождение переменной в формулу называется связанным, если оно непосредственно следует за квантором или находится в области действия квантора, в противном случае вхождение переменной называется свободным.
Предметная переменная называется свободной в некоторой формуле, если существует хотя бы одно свободное вхождение вхождение переменной в формуле.
Переменная называется связанной в некоторой формуле, если существует хотя бы одно связанное вхождение переменной в формулу.
Пример: x( yP(x,y,z) R(x,y,z) )
х- связанная, y- связанная и свободная, z- свободная
Замкнутый терм – не содержит переменных
Замкнутая формула – не содержит свободных переменных
В натуральном исчислении предикатов, если в формуле есть свободные переменные, то она недоказуема.
Определение правильной подстановки по Ильину:
1)подстановка идет вместо предметных переменных
2)подстановка идет вместо свободных предметных переменных
3)Подстановка идет вместо всех вхождений предметной переменной
4)Количество связанных вхождений после подстановки не изменится.
Определение правильной подстановки по Зайцеву: Подстановка терма вместо предметной переменной в формулу является правильной, если и только если переменная, входящая в терм, не окажется связанной на местах, где появится терм в результате подстановки.
9. Натуральное исчисление предикатов: правила вывода, понятия вывода, завершенного вывода и доказательства.
Схема, по которой строятся исчисления:
1 искусственный язык
2 множество дедуктивных принципов(либо аксиомы либо правила перехода от одних выражений к другим
аксиомы+правила. Аксиоматическое исчисление. Теорема – такое утверждение, которое получено из аксиом. Процедура определения является ли формула теоремой – аналог естественного рассуждения. Недостаток: нужно иметь много аксиом на все случаи жизни. |
Правила. Натуральное исчисление. Аксиом нет, роль аксиом выполняет множество правил вывода. Удобны для моделирования естественных человеческих рассуждений. |
А (α/β)-результат
правильной подстановки в формулу А
-введение

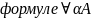
исключение - α A (α)
А(α/t) , где t – терм,
введение
 А(α/t)
исключение
-
αA
А(α/t)
исключение
-
αA
αA А (α/β) , β – абсолютно ограничена (а.о.)
β – ограничивает все свободные переменные в α A.
А(α/t) – рез-т правильной подстановки терма t вместо всех свободных вхождений переменной α.
введение

А(α/α)-тривиальная подстановка, она всегда правильна. Подстановка константы или замкнутого терма тоже всегда правильна.
Вывод – непустая конечная последовательность формул С1,С2,…,Сn, удовлетворяющая следующим условиям:
1. Каждая Сi есть либо посылка, либо получена из предыдущих формул по одному из правил вывода
2. Если в выводе применялись правила в или в, то все формулы, начиная с последней посылки и вплоть до результата применения данного правила исключаются из дальнейших шагов построения вывода
3. Никакая переменная не может быть абсолютно ограничена в выводе более одного раза
4. Никакая переменная не ограничивает в выводе саму себя
Доказательство – это вывод из пустого множества посылок.
Вывод называется завершенным, если в нем свободно не содержится никакая абсолютно ограниченная переменная.
Завершенное доказательство – это завершенный вывод из пустого множества посылок.
4 эвристика – если после применения первой эвристики целью является формула с квантором, то следует применять другие эвристики, не обращая внимания на квантор.
Условная интерпретация переменных и интерпретация всеобщности(безусловная).
x=x – интерпретация всеобщности, потому что на место х можем поставить все что угодно.
U=N(множество натуральных чисел) х-3=6 – условная интерпретация, наш выбор ограничен, только 9.
х-3 если
х/8 – выбор ограничен подстановкой
вместо х,
если
х/8 – выбор ограничен подстановкой
вместо х,
8-3 выбор
одной переменной ограничивает другие
переменные в формуле.
выбор
одной переменной ограничивает другие
переменные в формуле.
В том случае, когда переменная в составе формулы понимается как знак, обозначающий любой объект из универсума, про нее говорят, что она употреблена в этой формуле в интерпретации всеобщности. Выбор значения для переменной – это абсолютное ограничение переменной. 10. Аксиоматическое исчисление предикатов: схемы аксиом и правила вывода, понятия доказательства, и теоремы. Метатеоретические свойства классической логики.
Правила вывода:
A B, A - modus ponens
B
A -правило генерализации
αA
Доказательство – это вывод из пустого множества посылок.
Теорема – формула, доказуемая в аксиоматическом исчислении предикатов.
Выводом формулы В из посылок А1....Аn в аксиоматическом исчислении предикатов называется конечная непустая последовательность формул С1….Ск , в которой Ск есть формула В и эта последовательность удовлетворяет условиям:
1)Каждая Сi является или одной из посылок А1…Аn или аксиомой или получена из предыдущих про правилу МР или по правилу генерализации, которое применялось к переменным, не входящим свободно в посылки.
Метатеоретические свойства(по Ильину) – это свойства исчислений(делятся на МТ отношения и МТ свойства). Мт отношения – это связь между исчислением и семантической теорией. В исчисления теоремы, в теориях законы(общезначимые формулы).
Исчисление
называется семантически непротиворечивым
относительно теории Т, если все теоремы
данного исчисления являются законами
теории.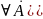 ├ A
├ A Тǀ=
А)
Тǀ=
А)
Исчисление S семантически полно относительно теории Т, когда любая общезначимая формула теории Т является теоремой исчисления S. A(Тǀ=А S˫A)
Если 2 условия выполняются, то исчисление является адекватной формализацией теории Т(семантическая адекватность).
МТ свойства, которые отношениями не являются:
Исчисление синтаксически непротиворечиво, когда в нем не найдется такая формула, что в исчислении доказуема она и ее отрицание.
Синтаксическая полнота: Исчисление является синтаксически полным, когда при добавлении к этому исчислению в качестве новой аксиомы любой недоказуемой в нем формулы, исчисление становится синтаксически противоречивым.
Логическое исчисление разрешимо, если существует эффективная процедура, позволяющая для любой формулы языка этого исчисления в конечное число шагов установить, является ли формула теоремой. МТ дедукции не является Мт свойством. Свойство семантической теории – функциональная полнота системы связок классической логики высказываний. (Это все по Ильину)
Таблица МТ свойств по Зайцеву:
|
К2 – аксиоматич. исчисление высказыв. со схемами аксиом |
К3 – аксиомат.исчисл.выск. с конечным числом аксиом и правилом подстановки |
П2-аксиомат.исчислен. предикатов со схемами аксиом |
П2=- исчисление предикатов с равенствами |
П22 – исчисление предикатов второго порядка |
Семантическая непротиворечивость |
+ |
+ |
+ |
+ |
+ |
Семантическая полнота |
+ |
+ |
+ |
+ |
- |
Синтаксическая непротиворечивость |
+ |
+ |
+ |
+ |
+ |
Синтаксическая полнота |
- |
+ |
- |
- |
- |
разрешимость |
+ |
+ |
- |
- |
- |
Дедуктивное свойство |
+ |
+ |
+ |
+ |
+ |
Еще одно МТ свойство – функциональная полнота системы связок классической логики высказываний.
11. Расширения исчисления предикатов первого порядка: логика предикатов с равенством, логика предикатов второго порядка.
Классическая логика предикатов первого порядка с равенством
а=а(аналитическое высказывание, всегда истинно, не несет информации в себе.
а=b – синтетическое высказывание, истинно только в каких-то моделях.
В алфавит языка логики предикатов добавляется новый символ = - 2-ух местный предикатор равенства.
В определении формулы появляется новый пункт
если t1 и t2 – это термы, то t1=t2 это формула.
 ǀt1=t2ǀϕ=И
ǀt1=t2ǀϕ=И ǀt1ǀϕ
и ǀt2ǀϕ
- совпадают.
ǀt1ǀϕ
и ǀt2ǀϕ
- совпадают.
Свойства равенства:
(α=α) – рефлексивность
а=b b=a - симметричность
a=b и b=c a=c – транзитивность.
Добавляются 2 новые схемы аксиом, они обеспечивают эти 3 свойства.
Можно ввести особый квантор существования – оператор существования единственного объекта(существует единственный объект, такой что..) Обозначим этот квантор 1. Тогда:
Е1
α А(α) ≡
α
(А (α) &
 (А(α)&
A(β)
α
= β ))
(А(α)&
A(β)
α
= β ))
Логика предикатов первого порядка по своим выразительным возможностям является все еще бедной системой. В ней можно выражать лишь утверждения о предметах и нельзя выражать каких-либо утверждений о свойствах предметов и отношениях между ними. Эта особенность логики предикатов первого порядка связана с тем, что в ней используются только предметные переменные и не используются переменные по свойствам, отношениям и функциям. В логике предикатов 2-ого порядка можно делать осмысленные утверждения о свойствах, отношениях и функциях.
в язык вводятся предикаторные переменные и предметно-функциональные переменные.
Pn Qn Rn fn gn kn – Записываются курсивом.
К понятию терма добавляется:
Фn (t1, t2,...tn)-терм если, t1, t2,...tn – термы, Фn - n-местная предметно-функциональная переменная.
Добавление к понятию формулы:
1. Пn (t1, t2,...tn). Пn - не только предикаторная константа, но может быть предикаторной переменной.
2. Если А – формула, а α – предметная переменная, то αA и αA – формулы. Теперь α может быть не только предметной, но и предикаторной и предметно-функциональной переменной.
α= ≡ P (P (α) ≡ P ( )) – 2 предмета тождественны, если у них совпадают все свойства. (Лейбниц)
0 (P) ≡┐Ех P (х) – некоторое свойство является нулем, если и только если не существует предметов, обладающих этим свойством.
1 (P
) =
х
(P(х)&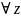 (P(z)
z=x))
– некоторое свойство является единицей,
если и только если существует ровно
один предмет, обладающий этим свойством.
(P(z)
z=x))
– некоторое свойство является единицей,
если и только если существует ровно
один предмет, обладающий этим свойством.
Константа истины Т и ее определение:
Т=
П Пх
– есть такое свойство и есть такой
предмет, обладающий этим свойством.(все
буквы пишутся в формуле курсивом).
Пх
– есть такое свойство и есть такой
предмет, обладающий этим свойством.(все
буквы пишутся в формуле курсивом).
Константа лжи ǀ и ее определение: ǀ = П х¬Пх – ни один предмет никаким свойством не обладает.(все буквы пишутся в формуле курсивом).
Но в логике предикатов 2-ого порядка мы мало можем доказать.
12.Метатеоретические свойства классической логики высказываний. Метод математической индукции, его разновидности.
Часть таблицы из 10 вопроса – это МТ свойства классической логики высказываний.
По Ильину: Исчисление высказываний с конечным числом аксиом и правилом подстановки. Это исчисление является адекватной формализацией логики высказываний(класс законов логики высказываний и теорем исчисления совпадают). Можно посмотреть есть ли эффективная процедура в логике высказываний для определения, является ли формула законом. Такая процедура есть – таблицы истинности. Докажем, что таблицы истинности – эффективная процедура:
1)По определению формулы(у нас нет формул бесконечной длины – доказывается отдельно).
2)Т.к нет формул бесконечной длины, то конечное число пропозициональных переменных(p,q,r,s)
3)Если конечное число пропозициональных переменных, то конечное число строк в таблице
4)Значит и в результирующей колонке конечное число строк.
5)Формула является законом, если в результирующей колонке нет значения ложь.
Т.к для любой формулы есть эффективная процедура определения ее общезначимости в логике высказываний, а класс законов в логике высказываний и теорем в исчислении совпадают, то исчисление является разрешимым.
Исчисление высказываний со схемами аксиом. Некорректно говорить о синтаксической полноте(относительно ее сформулированного определения) по отношению к указанному исчислению(в определении говорится о формулах, а у нас схемы формул). Т.е определение о синтаксической полноте к данному исчислению не применимо.
Натуральное исчисление высказываний. Некорректно ставить вопрос о синтаксической полноте, потому что у нас нет аксиом.
Математическая
индукция:
Индукция – разновидность правдоподобных
рассуждений. Полная математическая
индукция: Дано
͚(бесконечное)
счетное(можем пронумеровать элементы
множества) множество S.
Нужно показать, что все элементы S
обладают некоторым свойством Р.
 P(х)).
Метод доказательства: Базис: ˫Р(х1)
– первый элемент обладает свойством.
P(х)).
Метод доказательства: Базис: ˫Р(х1)
– первый элемент обладает свойством.
Индуктивное допущение:
n(n 1
P(Xn-1)).
1
P(Xn-1)).
Индуктивный шаг: ˫Р(Хn) – доказывается, что свойством Р обладает n-энный объект.
S P
1 P
2
.
.
+ n-1
P
n-1
P
n P
В общем виде: Р(х1), n((n 1 P(Xn-1)) P(Xn))
x(x S
P(x))
S
P(x))
Недостатки - И – шаги не по порядку при применении этого правила и поэтому существует разновидность математической индукции: Возвратная индукция(сильная математическая индукция) :
n( m(m n P(Xm)) P(Xn))
x(x S P(x))
13. Семантическая непротиворечивость и полнота классической логики высказываний.
Если 2 этих свойства присутствуют, то говорим о семантической адекватности – А(S˫A Tǀ=A)
Семантическая непротиворечивость аксиоматического исчисления высказываний со схемами аксиом.
А(К2˫А Тǀ=А)
Док-во:
+1. пусть К2|-- A
2. Существует доказательство формулы А в К2(из 1)
3. существует непустая конечная последовательность схем формул С1, С2…..Ск, где Ск – есть А, каждая схема формул Сi есть либо 1)схема аксиом 3)получена по правилу МР из предыдущих
4. Зафиксируем Ск и докажем метатеорему методом возвратной математической индукции.
Индуктивное допущение: m(m k Утверждение МТ верно для Сm), т.е
С1ǀ=С1
С2ǀ=С2
:
Сmǀ=Cm
Сk
Индуктивный шаг: покажем, что для Ск утверждение МТ верно. Док-во:
1)m=1(C1), C1 – схема аксиом. Покажем, что все схемы аксиом тождественно-истинны.
ǀ=А (В А)
и |
И |
И |
И |
И |
И |
И |
Л |
И |
И |
Л |
И |
И |
Л |
Л |
л |
и |
л |
и |
л |
2 )Пусть
к
1
и к
m
и утверждение МТ верно для
Сm.
Ck
схема
аксиом(2.1)
)Пусть
к
1
и к
m
и утверждение МТ верно для
Сm.
Ck
схема
аксиом(2.1)
получена из предыдущ. по МР(модус поненс) 2.2
2.1 равносильна 1
2.2. Cj(житое) - Сi Ck
Ci(итое)
Ск – по МР из I и j шагов
По индуктивному допущению, т.к i и j k, то ǀ=Сi Ckǀ=Ci
?ǀ=Ск
ǀ=Сi Ckǀ=Ci
и и и и
Правило МР сохраняет тождественную истину ǀ=Ск
5. Т.о А(К2˫А Тǀ=А)
Семантическая полнота.
A (Tǀ=A ˚S├ A)
14. Синтаксическая полнота и непротиворечивость классической логики высказываний.
˚ А(S ├ A &˚ S ├ A)-непротиворечивость
A
(S ˫A
 B
( S+A├
B &˚ S+A├
┐B)) – полнота
B
( S+A├
B &˚ S+A├
┐B)) – полнота
с интаксическая непротиворечивость: ˚ А(К2 ├ A &˚ К2 ├ A)-в аксиоматическои исчислении высказываний со схемами аксиом. Док-во:
+1. А( К2|--A & К2|-- ┐A) –допущение от противного
2.
К2|-- B &К2|--
┐B (из 1 по правилу
исключения квантора существования- )исключаем
по В
)исключаем
по В
3. К2|-- B (из 2 по правилу исключения &- &и)
4. К2|-- ┐B - &и:2
5. A (К2|--A Т|= A) ( метатеорема о семантической непротиворечивости)
6.
К2|-- B
Т|= B (из 5 по правилу
исключения квантора общности-
 )
)
7. Тǀ= B - МР 6 и 3
8
К2|-- ┐B
 |=
┐B -
|=
┐B -
9. Т|= ┐B - по МР из 8 и 4
10.Тǀ= В – из 9 по условиям истины для отрицания
11. ┐˚ А ( К2|--A &˚ К2 |-- ┐A) - ¬в: 7, 10
A (К2 ˫A B ( К2+A├ B &˚ К2+A├ ┐B))
+ 1. К2˫A
2.
 (Т|=
A
К2|--A) (метатеорема
о семантической полноте)
(Т|=
A
К2|--A) (метатеорема
о семантической полноте)
3.
Т|= А
К2+А - из 2

4. Тǀ=А - (из 1 и 3, по правилу modus tollens) - A B, ¬B
¬A
5. Существует набор значений α1, α2, …αn пропозициональных переменных Р1…Рn формулы А, на котором она принимает значение ложь – из 4 по определению тождественно-истинной формулы(пусть А=р q)
6. Осуществляем подстановку в формулу А вместо каждой переменной Рi (итой переменной), формулы Рi v¬ Рi, если αi=и и Рi&¬ Рi, если αi=л, получившуюся формулу обозначим А*
Лемма: Если формула А ложна на наборе α1, α2, …αn, то А* - тождественно-ложная формула
р q р/р v¬р q/q v¬q
и л л
А*( р v¬р) ( q v¬q)
И Л Л
7. А*- тождественно-ложная (из 6 по лемме)
8. Т|= ┐А* (из 7 по определению отрицания)
9. К2 |-- ┐А* (из 8, по метатеореме о семантической полноте)
10. К2+A |-- ┐А* (из 9, т.к К2+A – расширение К2 по свойствам выводимости. Монотонность Г˫С)
Г,А˫С
11. К2+A |-- A- по свойствам выводимости, рефлексивность А˫А
К2, А˫А
12. К2+A |-- А* - из 11, т.к А*- результат подстановки
13. К2+A |-- А* & К2+A |-- ┐А* - &в: 10, 12
14.
В
(К2+A |-- В & К2+A
|-- ┐В)-

15. К2 ˫A B ( К2+A |-- B & К2+A |-- ┐B) - в:14
16.
A
(К2 ˫A
B
( К2+A├
B &˚ К2+A├
┐B)) -
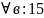
15. Метатеоретические свойства классической логики высказываний. Метатеорема дедукции.
МТ свойства те же самые что и в 12 вопросе.
Мт дедукции: Г,А˫В
Г˫А В
Докажем для исчисления К2. Доказательство методом возвратной индукции по длине вывода.
Док-во: Индуктивное допущение – для всех формул с номером m n утверждение МТ верно.
Индуктивный шаг: покажем, что утверждение МТ верно и для Сn. Используем определение вывода:
1) Сn-аксиома
2) Сn-посылка из Г
3) Сn – дополнительная посылка
4) Сn – получена по МР
1) Сn-аксиома
1.К2˫Сn (т.к Сn – аксиома)
2. Г,А˫Сn из 1 по свойствам выводимости(из любого множества Г формула выводима
3. построим вывод
Г˫А Сn(цель)
Г
1. Сn-аксиома
2. Сn (А Сn) – подстановка в А1: А (В А) - А/ Сn, В/А
3. А Сn -по МР из предыдущего
2) Сn – посылка из Г. Построим вывод: Г˫ А Сn(цель)
Г Сn Г,А˫ Сn
Сn (А Сn) – подстановка в А1
А Сn -по МР из предыдущего
3) Сn – доп.посылка, т.е Сn есть А(т.к А – доп.посылка)
строим вывод. Цель Г˫А А
Г
А А А – теорема в К2
˫ А А
1.А ((А А) А) (А (А А)) (А А) – подстановка в А2. В/ А А, С/А
2. А ((А А) А) – подстановка в А1. В/А А
3. (А (А А)) (А А) – МР 1, 2
4. А (А А) – подстановка в А1 В/А
5. А А – МР 3, 4
4) Сn – получена по МР. Рассмотрим вывод Сn из Г, А
Г
А
j Ci
I Ci Cn
Cn
поскольку итый и житый шаги n, то для соответствующих формул Мт Дедукции верна(по индуктивному допущению.
Г
Г˫А (Сi Cn)
1. А Сi
2. А (Сi Cn)
3. осуществим подстановку в А2- В/ Сi, С/ Cn – (А (Сi Cn)) ( (А Сi) (А Сn))
4. (А Сi) (А Сn) – МР из предыдущего т.е из 3, 2
5. А Сn – МР из 1, 4
4 случая рассмотрены, индуктивный шаг доказан, следовательно МТ дедукции доказана. Следствие Мт дедукции:
А˫В
˫А В – является теоремой
16. Метатеоретические свойства классической логики предикатов. Метод математической индукции, его разновидности.
Мт свойства – часть таблицы свойств.
МТ свойства классической логики предикатов по Ильину:
Исчисление
предикатов с конечным числом аксиом –
не является синтаксически полным(т.е
можно добавить формулы, которые не
являются теоремами и исчисление не
станет противоречивым. Например:
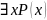
 ).
Не является разрешимым(доказана теорема
о неразрешимости исчисления предикатов).
На конечных областях исчисление
предикатов разрешимо.
).
Не является разрешимым(доказана теорема
о неразрешимости исчисления предикатов).
На конечных областях исчисление
предикатов разрешимо.
Исчисление предикатов со схемами аксиом: Не корректно ставить вопрос о синтаксической полноте в той формулировке, в которой она дана. Не разрешимо.
Натуральное исчисление предикатов – тоже самое что и в предыдущем. Не корректно говорить о синтакс. полноте, потому что нет аксиом в исчислении.
В данных исчислениях доказывается МТ дедукции. Мт дедукция – это не метатеоретическое свойство. Мат. индукция по Ильину: Прямая мат. индукция- если первый элемент множества обладает свойством, и в случае, что этим свойством обладает какой-то элемент множества, свойством обладает и последний элемент множества. Возвратная мат. индукция: допускаем, что свойством обладает меньший порядковый номер и доказываем, что оно верно для большего порядкового номера.
(Еще Мат.индукция в 12 вопросе).
