1.2.3 Операции во временной области

 

Рассмотрим последовательность коэффициентов отражения, представленную временным рядом (1, 0, ). Рассмотрим также импульсный источник, который дает взрыв на время t=0 с амплитудой 1. Отклик последовательности коэффициентов отражения на импульс называется импульсным откликом (impulse response). Этот физический процесс может быть описан следующим образом:

Через одну единицу времени предположим, что источник формирует импульс (impulsion) с амплитудой - . Этот процесс описывается следующим образом:

Обратите внимание, что отклик представляет собой последовательность коэффициентов отражения, масштабированную интенсивностью импульса. Поскольку функция источника рассматривается как последовательность взрывных импульсов и импульсов, вызванных резким уменьшением давления в ограниченном объеме (implosive impulses), отдельные импульсные отклики складываются с целью получения комбинированного отклика. Этот процесс называется линейной суперпозицией и описан в таблице 1-1.

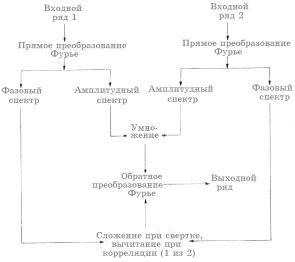
Рис.1-17 Форма нуль-фазового импульса (а) может быть модифицирована путем введения не нуль-фазового спектра любой формы (изображения b, c, d).

 

В таблице 1-1 звездочка обозначает свертку. Отклик последовательности коэффициентов отражения (1, 0, ) на импульс источника (1, ) ,был получен путем свертки двух последовательностей. Это выполняется путем расчетов, как показано в таблице 1-2.

Фиксированный ряд задан по последовательности коэффициентов отражения. Импульс источника обращается (складывается) и перемещается (задерживается) на одну выборку за один раз. При каждой задержке выровненные элементы перемножаются и полученные произведения складываются. Механизм сверки показан в таблице 1-3. Количество элементов выходного ряда c(k) задается как m + n – 1, где m и n – длины соответственно ряда операндов a(i) и ряда операторов a(j).

Когда функции рядов в таблице 1-2 меняются местами, получается ряд, показанный в таблице 1-4. Выходная характеристика получается такая же, как в таблице 1-2. Следовательно, не имеет значения, какой ряд при свертке является фиксированным, а какой – скользящим.

Сейсмическая обработка часто требует измерения сходства или выравнивания времен двух трасс. Корреляция представляет собой другую операцию во временной области, которая используется для импульса:

Импульс 1: (2, 1, -1, 0, 0)

Импульс 2: (0, 0, 2, 1, -1)

Хотя эти импульсы идентичны по форме. Импульс 2 смещен на 2 выборки относительно импульса 1. Можно определить временную задержку, при которой импульсы будут иметь наибольшее сходство. Для этого выполним операцию на импульсе 1, как описано в таблице 1-3, не обращая импульс 2 (т.е. шаг 0 пропускается). Это называется взаимной корреляцией, результат которой показан в таблице 1-5. Взаимная корреляция измеряет степень сходства двух последовательностей. Взаимная корреляция временной последовательности с ней самой называется автокорреляцией.

Из таблицы 1-5 видно, что максимальная корреляция наблюдается при задержке, равной –2. Это предполагает, что импульс 2 был смещен на две выборки назад во времени, эти два импульса (импульс 1 и импульс 2) будут иметь максимальное сходство.

Таблица 1-6 показывает значения взаимной корреляции. Являющиеся результатом перестановки рядов местами. Теперь максимальная корреляция наблюдается при задержке равной 2. Следовательно, если импульс 1 смещается во времени на две выборки вперед, эти два импульса будут характеризоваться максимальным сходством. Отметим также, что, в отличии от свертки, взаимная корреляция не обладает свойством коммутативности, т.е. результат зависит от того, какой ряд является фиксированным, а какой – скользящим (сравните результаты в таблицах 1-5 и 1-6).

В таблице 1-7 показаны задержки автокорреляции импульса 1. Отметим, что максимальная корреляция имеет место при нулевой задержке – это важное свойство автокорреляции. Более того функция автокорреляции является симметричной: это свойство действительной временной последовательности. Следовательно, необходимо рассчитывать только одну сторону ФАК.

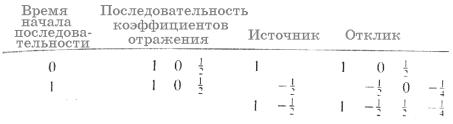
В разделе 1.2.4 показано с эвристической точки зрения, что свертка во временной области эквивалентна умножению в частотной области (Bracewell, 1965). Поскольку корреляция представляет собой свертку без обращения скользящего ряда (см. таблицу 1-3), к корреляции также применяется сходная операция в частотной области. На рис.1-18 в обобщенном виде дается описание свертки и корреляция в частотной области.

 

Таблица 1-1 Линейная суперпозиция.

Суперпозиция:

В другом виде: (1, 0, )*(1, - ) = (1, - , , - )

 Таблица 1-2 Сверка импульса источника (1, - ) с последовательностью коэффициентов (1, 0, ).

 

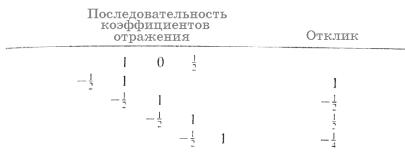
Таблица 1-3 Механика процесса сверки.

Фиксированный ряд:

а(1) а(2) а(3) а(4) а(5) а(6) а(7) а(8)

Скользящий ряд:

b(1) b(2) b(3)

При двух данных рядах а(i) и b(j):

Шаг 0 = обратить скользящий ряд b(j).

Шаг 1 = выполнить умножение по вертикали.

Шаг 2 = сложить произведения и записать в виде результирующей точки c(k).

Шаг 3 = сместить ряд b(j) на одну выборку вправо и повторить шаги 1 и 2

Таблица 1-4 Свертка последовательности коэффициентов отражения (1, 0, ) с импульсом источника (1, - ).

 

Таблица 1-5 Взаимная корреляция импульса 1 с импульсом 2.

 

Таблица 1-6 Взаимная корреляция импульса 2 с импульсом 1.

 

Таблица 1-7 Автокорреляция импульса 1.

 

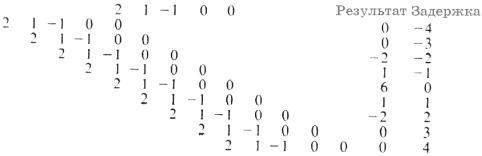
Рис.1-18 Описание свертки и корреляции в частотной области.

Из рис.1-18 видно, что свертка и корреляция дают результат, спектральная полоса пропускания которого является общей для обеих входных последовательностей. Примером может служить процесс полосовой фильтрации. Отметим также, что фазы являются аддитивными при свертке и субтрактивными при корреляции (Bracewell, 1965). Для автокорреляции это означает, что выходная последовательность является нуль-фазовой. Этот факт уже был проверен примером в таблице 1-7, где показано, что ФАК является симметричной относительно нулевой задержки. Взаимная корреляция широко используется в качестве меры сходства на различных стадиях обработки данных.

Например, рассчитывается ФВК трасс в выборке ОСТ (общих средних точек) с опорной трассой с целью расчета смещений, вызванных остаточной статикой (см. Раздел 3.4). Основой для расчета скоростного спектра также является взаимная корреляция. “Компновочные блоки” фильтра Винера (раздел 2.6) представляют собой взаимную корреляцию желательного импульса на выходе со входным импульсом и корреляцию входного импульса.

Другим важным процессом является корреляция вибросейса. Сюда входит взаимная корреляция частотно-модулированного сигнала источника (свип-сигнал) с зарегистрированной трассой вибросейса. Свип-сигнал представляет собой частотно-модулированный сигнал вибросейса, подаваемый в разрез. Модуль фильтрации для вибросейсмических данных рассмотрен в разделе 2.7.7. На рис.1-19 показан свип-сигнал, зарегистрированная выборка ОПВ и коррелированная выборка. Длина свип-сигнала равна 10с, полоса частот – от 6 до 60Гц. 15-секундная некорректированная запись вибросейса дает 5-секундную коррелированную запись. Отметим, что верхняя часть некоррелированной записи содержит низкочастотную энергию; в нижней части записи повышается содержание высоких частот. Это связано с тем, что в этом примере данных было использовано свипирование в направлении роста частот.