1. Теоретическая часть.

1. Закон распределения Симпсона.

Закон распределения Симпсона (рисунок 1) является композицией двух одинаковых законов с равномерной плотностью распределения. Вид плотности распределения вероятностей по закону Симпсона приведен на рисунке 1, ей соответствует аналитическое описание.

Рисунок 1

при

при

при

2. Метод Бусленко.

Для получения случайных чисел с любым заданным законом распределения наиболее универсальным является метод кусочной аппроксимации, предложенный Н.П. Бусленко.

Он может быть использован для генерации случайных величин в интервале ().

Для этого кривую плотности вероятности разбивают на n участков с интервалами (). Вероятность попадания в каждый интервал обозначим , причем

В пределах данного интервала можно считать плотность распределения случайной величины f(x) постоянной, случайную величину X распределенной равномерно. Плотность распределения f(x) разбивается на участки таким образом, чтобы вероятность попадания туда случайной величены была постоянной, и не зависела от номера интервала

.

Тогда

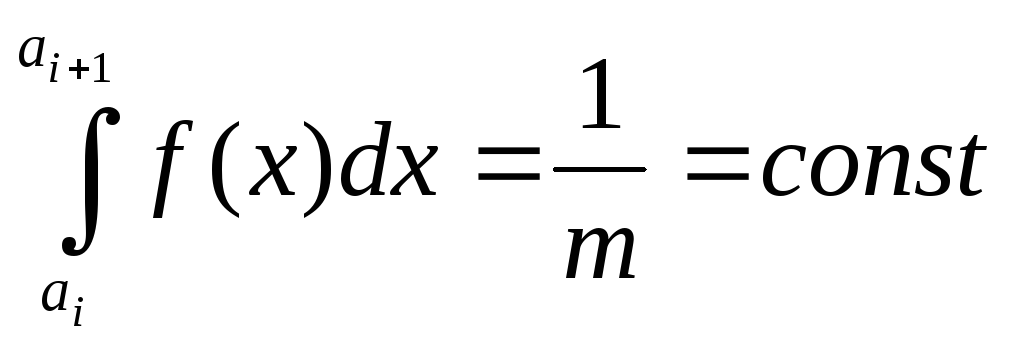
Что значит, что площади прямоугольников равны и разыгрывание номера интервала можно производить с помощью генератора случайных чисел с равномерным законом распределения.

Алгоритм вычисления границ интервалов:

1. вычисляется площадь под кривой плотности распределения на интервале

;

2. вычисляется текущая площадь для определения первой границы

.

Граница будет равна значению x, для которого выполняется условие

.

Аналогичным образом определяются все границы интервалов , которые образуют определенный массив данных.

Следовательно, заданный закон распределения в зависимости от вида плотности распределения влияет на расположение границ интервалов . Внутри интервалов случайная величина распределена по равномерному закону распределения.

После формирования массива производится генерация совокупности чисел, распределенных по заданному закону. Для этого выполняются следующие операции:

1. генерируется равномерно распределенное число из интервалов (0,1)

которое определяется случайным образом номер интервала ;

2. генерируется случайное число , по которому формируется случайная величина x, равномерно распределенная в интервале

,

где - масштабный коэффициент, определяется границами интервала.

Случайная величина имеет заданный закон распределения.

Реализация метода кусочной аппроксимации требует небольшого количества операции, которое не зависит от точности аппроксимации, т.е. от количества интервалов аппроксимации.

3. Оценка качества последовательности по гистограмме распределения.

Пусть получено N количество чисел. Весь интервал разбивается на m интервалов.

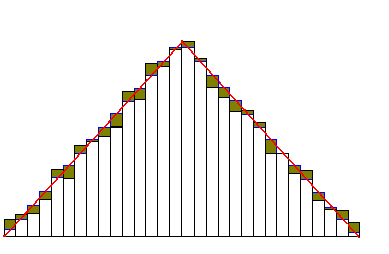
- вероятность попадания в j-ый интервал.

- относительная частота.

- высота прямоугольника на каждом интервале.

- длина каждого из интервалов.

- площадь j-ого треугольника.

- суммарная площадь под гистограммами.

- разница между теоретической и практической площадью.

Принятие решения о качестве ГСЧ и равномерности полученной последовательности осуществляется по соотношению:

не больше 5-10%.

Если условие выполняется, то распределение является равномерным.

На точность результата влияет:

• объем выборки 500 и больше;

• число интервалов;