11

Реферат

В данной курсовой работе был разработан генератор, генерирующий сигналы, распределенные по закону Вейбуло-Гнеденко со средним значением 30 минут и  = 8 минут.

Содержание

Введение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

1 Теория. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

2 Листинг программ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .10

3 Тесты . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15

Заключение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

Список литературы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .17

Введение

В практике моделирования систем наиболее часто приходится иметь дело с объектами, которые в процессе своего функционирования содержат элементы стохастичности внешней среды. Поэтому основным методом получения результатов с помощью имитационных моделей таких стохастических систем является метод статисчического моделирования на ЭВМ, используюший в качестве теоритической базы предельные теоремы теории вероятности.Возможность получения пользователем модели результатов статистического моделирования сложных систем в условиях ограниченности машинных ресурсов существенно зависит от эффиктивности процедур генерации псевдослучайных последовательностей на ЭВМ, положенных в основу имитации воздействий на элементы моделируемой системы.Для получения представляющих интерес оценок характеристик моделируемой системы S с учетом воздействий внешней среды Е статистические данные обрабатываются и классифицируются с использованием методом математической статистики.

Теоритической основой статистического моделирования систем на ЭВМ являются предельные теоремы теории вероятности. Множества случайных явлений подчиняются определенным закономерностям, позволяющим не только прогнозировать их поведение, но и количество оценить некоторые средние их характеристики. Принципиальное значение предельных теорем состоит а том, что они гарантируют высокое качество статистических оценок при весьма большом количествеиспытаний N.

Статистическое моделирование систем на ЭВМ требует формирования значений случайных величин, что реализуется с помощью генераторов случайных чисел. Результаты статистического моделирования существенно зависят от качества базовых последовательностей случайных чисел. Поэтому наличие простых и экономичных способов формирования, последовательностей случайных чисел требуемого качества во многом определяет возможность практического использования машинного моделированиясистем.

1 Распределение Вейбуло-Гнеденко.

Этот закон характерен для моделей с так называемым “слабым звеном”. Если система состоит из группы независимых элементов, отказ каждого из которых приводит к отказу всей системы, то в такой модели рассматривается распределение времени (или пробега) достижения предельного состояния системы как распределение соответствующих минимальных значений отдельных элементов: х_с = min(x₁; x₂; … x_n). Функция распределения этой величины может быть выражена следующей зависимостью:

где a и b – параметры распределения.

Примером использования распределения Вейбулла – Гнеденко является распределение ресурса или интенсивности изменения параметра технического состояния КЭ автомобиля, которые состоят из нескольких элементов, составляющих цепь.

По аналогичной схеме происходит регулирование тепловых зазоров клапанного механизма ГРМ. Некоторые изделия при анализе модели отказа могут быть рассмотрены как состоящие из нескольких элементов (участков): прокладки, уплотнения, шланги, трубопроводов, приводных ремней и т. д. Разрушение указанных изделий происходит в разных местах и при разной наработке, однако ресурс изделия в целом определяется наиболее слабым его участком, т. е. х_с = min(x₁; x₂; … x_n).

1.2 Метод обратной функции.

2 Листинг программы

Uses Crt, Graph, Sprites, Keyboard, Math, Strings, BmpRW, Shifrs;

label 1;

const Point_Count=1500;

Sigma=0.6;

Count_Dis=185;

var

j, t, Gd, Gm: integer;

Fj:array[0..Point_Count] of real;

Dlina_Dis, xx:real;

n:array[0..Point_Count] of longint;

Sum_Teor, Sum_Prac:real;

Bmp:BmpFile;

function RealToStr(A:real):string;

var S:string;

begin

S:='';

Str(A:9:9,S);

RealToStr:=S;

end;

function Teor(A,B:longint):Extended;

var Result,P: Extended;

ErrCode: Longint;

begin

P:=0;

for t:=A to B do

begin

Evaluate('('+IntToStr(t)+')^0.8', Result, ErrCode);

if ErrCode <> 0 then begin writeln('Invalid expression');bip;wait;end;

P:=P+1+2*Result*Exp(-2*Result-1);

end;

Teor:=P;

end;

function Time(j:longint):real;

var

Result: Extended;

ErrCode, Cod: Longint;

Value:Extended;

r_str:string;

begin

Value:=0;

Str(Ln(Fj[j]):9:9,r_str);

Evaluate(' (-'+r_str+'/2)^1.25 ', Result, ErrCode);

if ErrCode = 0 then

begin r_str:=Fls(Result); Val(r_str,Value,Cod); Time:=Value; end else

Writeln('Invalid expression');

end;

function x(j:longint):real;

begin

if (1-Fj[j]<>0) then x:=Sigma*SQRT(Ln(1/SQR(1-Fj[j])));

end;

function y(j:longint):real;

begin

y:=(x(j)/SQR(Sigma))*EXP(-SQR(x(j))/(2*SQR(Sigma)));

end;

function ProcPogr:real;

begin

Sum_Teor:=Teor(0,640);

Sum_Prac:=0;

for j:=0 to Count_Dis do

Sum_Prac:=Sum_Prac+Dlina_dis*n[j];

ProcPogr:=(Sum_Teor*100)/Sum_Prac;

end;

begin

SetSVGAMode(640,480,16,0);

MultiKeysInit;

// InstalBmp(0,0,Bmp);

{ OBmp('bmp.bmp',Bmp);

PutBmp(0,0,Bmp);}

1:

ChangePage;

randomize;

FillChar(n, SizeOf(n), 0);

for j:=0 to Point_Count do

Fj[j]:=random;

Dlina_Dis:=Point_Count div Count_Dis;

for j:=0 to Point_Count do

begin

xx:=Time(j);

PutPixel(round(Fj[j]*600),round(GetMaxY-Time(j)*100),RGBColor(255,0,255));

for t:=0 to Count_Dis-1 do

if ((t*Dlina_Dis <= xx*300) and (xx*300 < (t*Dlina_Dis+Dlina_Dis) ))

then inc(n[t]);

end;

SetColor(RGBColor(0,255,0));

for t:=0 to Count_Dis do

Rectangle(round(t*Dlina_Dis),round(479-n[t]*3), round(t*Dlina_Dis+Dlina_Dis)-1,479);

Line(0,479,640,479,$FFF);

Line(0,479,0,0,$FFF);

SetColor(RGBColor(255,255,0));

gotoxy(1,1);OutTextXY(10,10,'Teor='+RealToStr(Sum_Teor)+' Pract='+ RealToStr(Sum_Prac)+' Pogr='+ RealToStr(ProcPogr)+'%');

if TestKey(Esc_Scan) then halt;

if page then

begin

if page then if TestKey(Space_Scan) then wait;

if TestKey(F1_Scan) then begin SaveFromScr('bmp4.bmp',Bmp,0,0,GetMaxX,GetMaxY);wait;bip;halt;end;

end;

goto 1;

end.

3 Тесты

Для 20 точек были получены следующие значения случайных чисел:

Точка	Значение	Точка	Значение	Точка	Значение	Точка	Значение
1	28.56	6	25.52	11	27.28	16	35.52
2	17.68	7	29.52	12	18.96	17	24.08
3	25.52	8	30.88	13	29.36	18	31.12
4	18.64	9	24.24	14	16.64	19	32.4
5	20.16	10	19.52	15	28.56	20	19.04

Для 1000 точек и 30 интервалов разбиения были получены следующие значения:

Интервал	1	2	3	4	5	6	7	8	9	10
Число попаданий	6	10	23	15	23	23	45	53	68	62
Интервал	11	12	13	14	15	16	17	18	19	20
Число попаданий	86	88	102	86	92	87	87	87	61	52
Интервал	21	22	23	24	25	26	27	28	29	30
Число попаданий	45	32	29	24	14	19	3	7	1	2

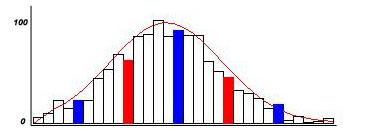
Рис. 2 Гистограмма закона распределения

Максимальное значение величины 41.68, минимальное - 13.36, среднее - 25.45, полученное значение Сигма - 5.224

Проверка осуществлялась по критерию Пирсона. Полученный результат Хи²: 16.0149 удовлетворяет табличному значению 40,113 при уровне значимости q=5%.

Заключение

В данной курсовой работе был разработан генератор, генерирующий сигналы, распределенные по закону Вейбуло-Гнеденко со средним значением 30 минут и Бэтта = 0,8.Отклонение распределения генератора не превышает 6% от теоретической.

Список литературы

1. Вентцель Е.С., Овчаров Л.А. Теория вероятностей и её инженерные приложения, М: Наука, 1988.

2. Вентцель Е.С. Исследование операций, М:Наука, 1980.

3. Лифшиц А.Л. Статистическое моделирование СМО, М., 1978.

4. Советов Б.А., Яковлев С.А. Моделирование систем, М: Высшая школа, 1985.

5. Гмурман В.Е. Теория вероятностей и математическая статистика, М: Высшая школа, 2001.