Шрёдингеровское описание
Математический аппарат нерелятивистской квантовой механики строится на следующих положениях:
Чистые состояния системы описываются ненулевыми векторами
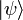комплексного сепарабельного гильбертова
пространства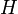 
,
причем векторы 
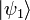и 
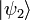описывают
одно и то же состояние тогда
и только тогда,
когда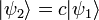 
,
где 
—
произвольное комплексное число.Каждой наблюдаемой можно однозначно сопоставить линейный самосопряжённый оператор. При измерении наблюдаемой
,
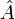при чистом состоянии системы
в
среднем получается значение, равное
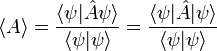
где
через 
обозначается
скалярное произведение векторов
и 
.
Эволюция чистого состояния гамильтоновой системы определяется уравнением Шрёдингера
где 
— гамильтониан.
Основные следствия этих положений:
При измерении любой квантовой наблюдаемой, возможно получение только ряда фиксированных её значений, равных собственным значениям её оператора — наблюдаемой.
Наблюдаемые одновременно измеримы (не влияют на результаты измерений друг друга) тогда и только тогда, когда соответствующие им самосопряжённые операторы перестановочны.
Эти положения позволяют создать математический аппарат, пригодный для описания широкого спектра задач в квантовой механике гамильтоновых систем, находящихся в чистых состояниях. Не все состояния квантовомеханических систем, однако, являются чистыми. В общем случае состояние системы является смешанным и описывается матрицей плотности, для которой справедливо обобщение уравнения Шрёдингера — уравнение фон Неймана (для гамильтоновых систем). Дальнейшее обобщение квантовой механики на динамику открытых, негамильтоновых и диссипативных квантовых систем приводит к уравнению Линдблада.
[Править]Стационарное уравнение Шрёдингера
Пусть 
амплитуда
вероятности нахождения
частицы в точке М.
Стационарное уравнение Шрёдингера
позволяет ее определить.
Функция
удовлетворяет
уравнению:
где 
—оператор
Лапласа,
а 
— потенциальная
энергия частицы
как функция 
.
Решение стационарного уравнения
Принцип неопределённости Гейзенберга
Соотношение неопределённости возникает между любыми квантовыми наблюдаемыми, определяемыми некоммутирующими операторами.
Неопределенность между координатой и импульсом
Пусть 
— среднеквадратическое
отклонение координаты
частицы 
,
движущейся вдоль оси 
,
и 
—
среднеквадратическое отклонение
ее импульса.
Величины
и
связаны
следующим неравенством:
где 
—
постоянная Планка, а 
Согласно
соотношению неопределённостей, невозможно
абсолютно точно определить одновременно
координаты и скорость частицы. Например,
чем больше точность определения
координаты частицы, тем меньше точность
определения ее скорости.
Неопределенность между энергией и временем
Пусть ΔЕ — среднеквадратическое отклонение энергии частицы, и Δt — время, требуемое для обнаружения частицы. Время Δt для обнаружения частицы с энергией E±ΔЕ определяется следующим неравенством:
Необычные явления, мысленные эксперименты и парадоксы квантовой механики
Соотношение неопределённостей Гейзенберга
Корпускулярно-волновой дуализм
Дифракция электронов
Сверхтекучесть (Бозе-конденсат)
Сверхпроводимость
Квантовая телепортация
Квантовая запутанность (Квантовая нелокальность, «Квантовое Вуду»)
Парадокс Эйнштейна — Подольского — Розена
Парадокс Клейна
Квантовый парадокс Зенона («Парадокс незакипающего чайника», связанный с аксиомой идеального измерения)
Кот Шрёдингера
Надбарьерное отражение
Теорема о запрете клонирования
Обменное взаимодействие