Содержание.

Задание…………………………………………………………………………………..2

1. Численное моделирование системы методом Эйлера…………………………………………………………………………………...3

Переход от динамических звеньев к дифференциальным уравнениям…………………………………………………………………………3

Численное моделирование системы в MatLab. Построение графика переходного процесса…………………………………………………………………………….4

Анализ переходного процесса……………………………………………………..5

Выводы……………………………………………………………………………...6

2. Исследование реальных механических процессов заданного объекта управления путём составления его математической модели…………………………………………………………………………………..7

Декомпозиция системы……………………………………………………...........8

Построение графа связей физических величин……………………………………………………………………..………11

Передаточные функции элементарных звеньев..................................................12

Структурная модель системы…………………………………………………..13

Построение структурной схемы в MATLAB.………………………………………………………...............................14

Графики переходных процессов…………………………………………………15

Вывод……………………………………………………………………………...17

Список литературы…………………………………………………………………..18

Задание:

Вариант 62.

Задание 1.

На рисунке приведена математическая модель системы управления положением.

Y - положение,

V - электрический сигнал,

V1 - скорость.

Провести численное моделирование системы методом Эйлера.

Задание 2.

P=10 H

m1=1 кг

m2=2 кг

m4=2 кг

m6=3 кг

l=0.4 м

r2=0.1 м

r4=0.2 м

C=4000 Н/м

1. Численное моделирование системы методом Эйлера.

Переход от динамических звеньев к дифференциальным уравнениям.

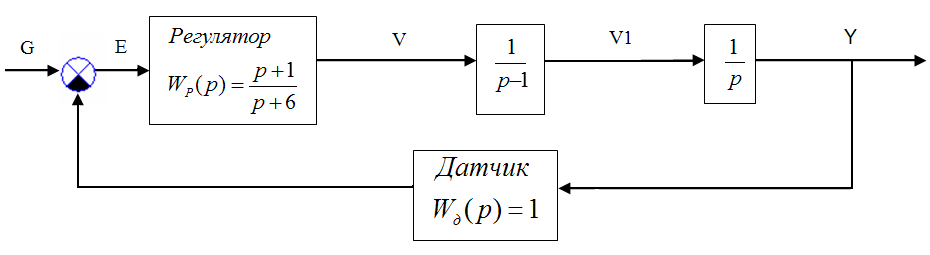
Рис.1. Математическая модель системы управления положением.

Y - положение,

V - электрический сигнал,

V1 - скорость.

Необходимо провести численное моделирование системы методом Эйлера.

По методу Эйлера следующая точка переходного процесса вычисляется по формуле:

.

Запишем уравнения связей необходимые для моделирования.

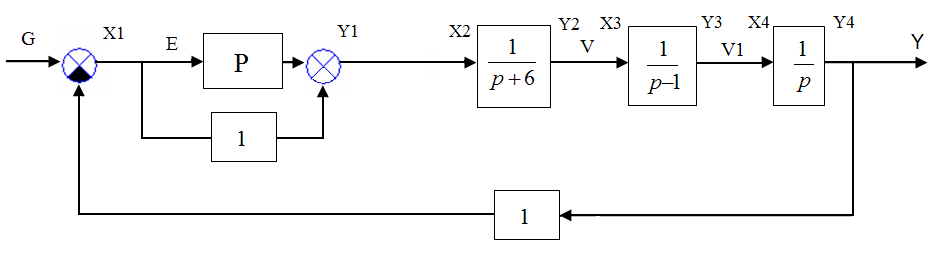
Рис.2. Структурная схема.

Обозначим:

X1=G-Y4=E;

X2=Y1;

X3=Y2=V;

X4=Y3=V1;

Y4=Y;

Из передаточных функций звеньев получаем следующие уравнения производных:

pY1 = (X1 - X0) + X1 = 2*X1-X0;

pY2 = X2 - 6*Y2;

pY3 = X3+Y3;

pY4 = X4;

X0 – приращение координаты за единицу времени.

Численное моделирование системы в MatLab. Построение графика переходного процесса.

На основе выше полученных данных составляем текст программы на MatLab.

По данному алгоритму получим график переходного процесса:

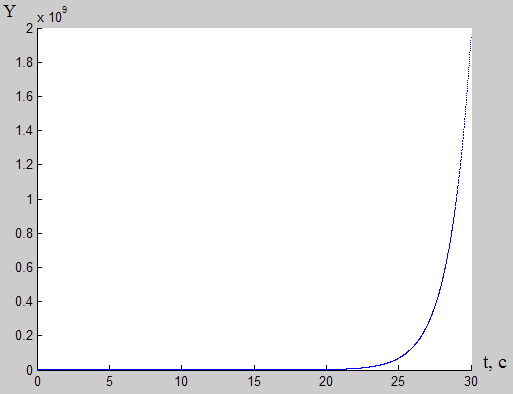
Рис.3. График переходного процесса.

Анализ переходного процесса:

В системе нет установившегося значения, отсутствует колебания, отсутствует перерегулирование.

Выводы:

Было проведено моделирование системы методом Эйлера. Для этого из типовых динамических звеньев заданных в математической модели объекта управления записали уравнения производных этих звеньев, а на их основе составили текст программы в MatLab, где построили график переходного процесса при управляющем воздействии равном единице.

2. Исследование реальных механических процессов заданного объекта управления путём составления его структурной схемы.

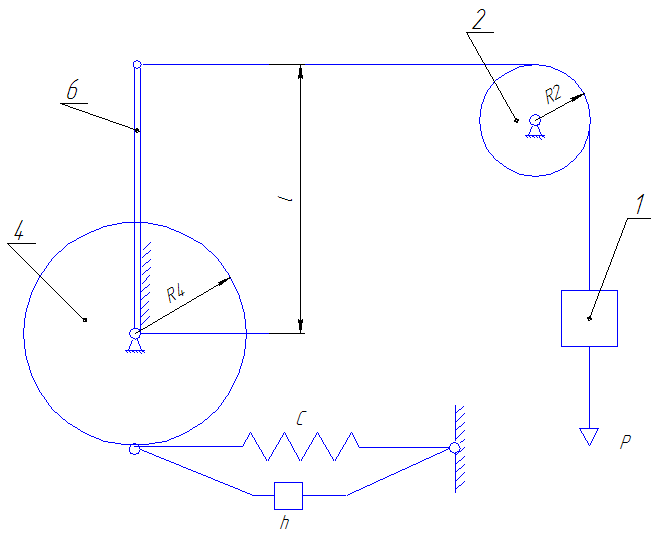
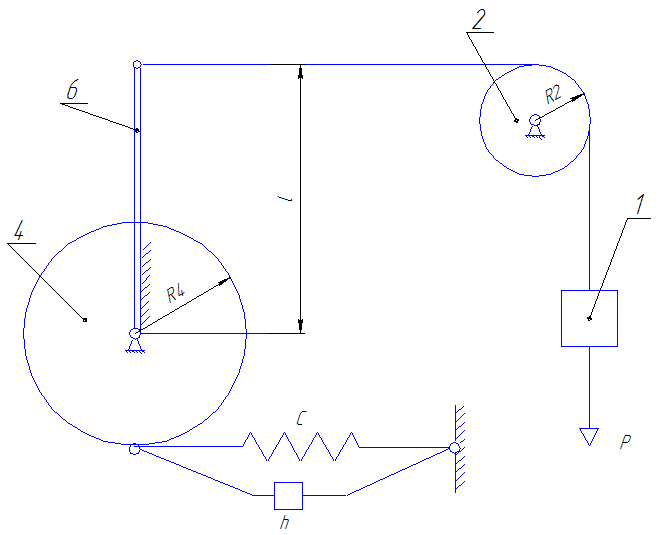
Рис.4. Исследуемое механическое устройство.

Дано:

P=10 H

m1=1 кг

m2=2 кг

m4=2 кг

m6=3 кг

l=0.4 м

r2=0.1 м

r4=0.2 м

C=4000 Н/м

Декомпозиция системы.

Выполним декомпозицию механического устройства на элементарные подсистемы, рассмотрим взаимосвязи между этими подсистемами и их взаимное влияние.

Подсистема1:

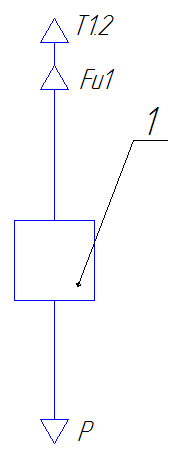
Рис.5. Первая подсистема.

Запишем уравнения равновесия сил:

P = T1.2 + Fu1,

где:

- сила инерции блока №1;

Р – внешняя сила (Н);

T1.2 – сила натяжения нити между блоками №1 и №2;

Подсистема 2:

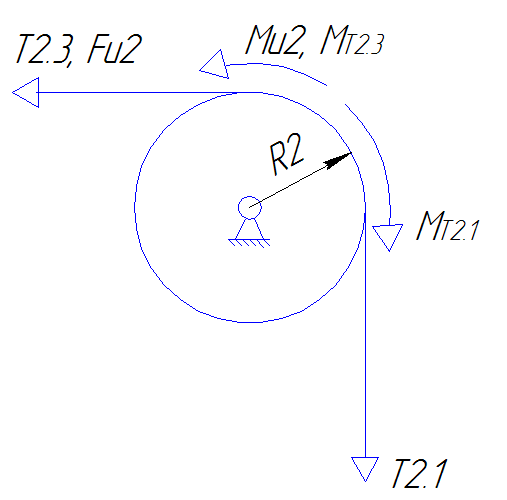
Рис.6. Вторая подсистема.

Запишем уравнения равновесия сил:

T2.3 + Fu2=T2.1,

Запишем уравнения равновесия моментов:

Mu2 + M_T2.3=M_T2.1,

где:

T2.3 - сила натяжения нити между блоками №2 и №3;

T2.1 - сила натяжения нити между блоками №2 и №1;

Fu2=m2*a2 - сила инерции блока №2;

- момент инерции блока №2, где ;

M_T2.3=T_2.3*R₂ - момент от силы натяжения нити между блоками №2 и №3;

M_T2.1=T_2.1*R₂ - момент от силы натяжения нити между блоками №2 и №1;

Подсистема 3:

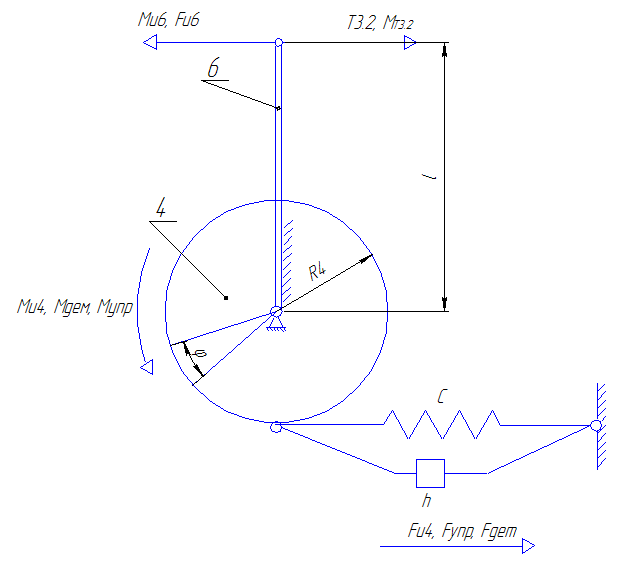
Рис.7. Третья подсистема.

Запишем уравнения равновесия сил:

T3.2 = Fu6 + Fu4 + Fупр + Fдем,

Запишем уравнения равновесия моментов:

M_T3.2 = Mu6 + Mдем + Mупр + Mu4,

где:

T3.2 - сила натяжения нити между блоками №3 и №2;

Fu6 = m6*a6 - сила инерции балки №6;

Fu4 = M₄/R4 - сила инерции блока №4;

Fупр = С*(R4*φ4) - сила демпфирования;

Fдем = h*(R4*ω4) = h*(R4* φ4) - сила упругости пружины;

M_T3.2 ==T_3.2*R4 - момент от силы натяжения нити между блоками №2 и №3;

- момент инерции балки №6, где ;

- момент инерции блока №4, где ;

Mдем = Fдем*R4 - момент от силы демпфирования;

Mупр = Fупр*R4 - момент от силы упругости пружины.

Построение графа связей физических величин.

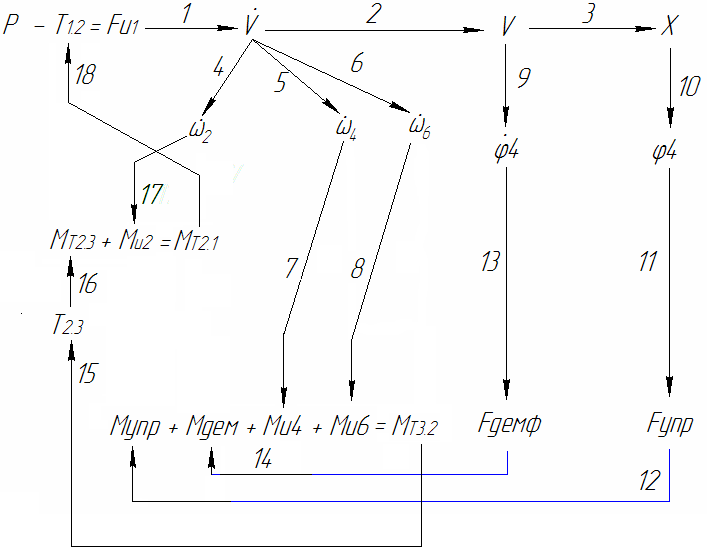
Рис. 8. Граф связей физических величин.

Передаточные функции элементарных звеньев:

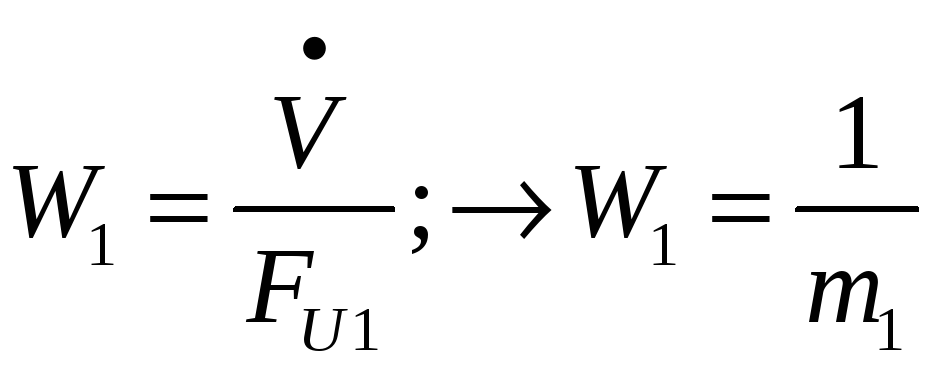
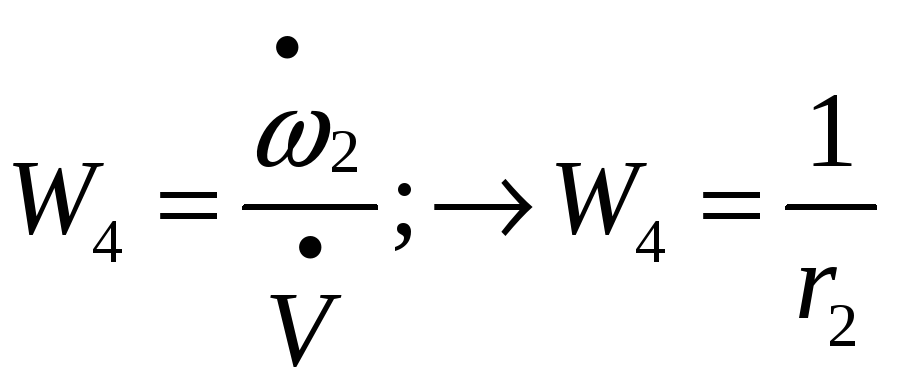
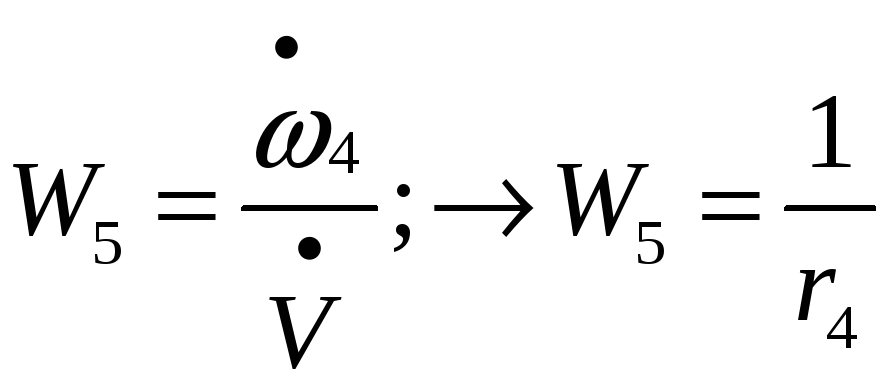
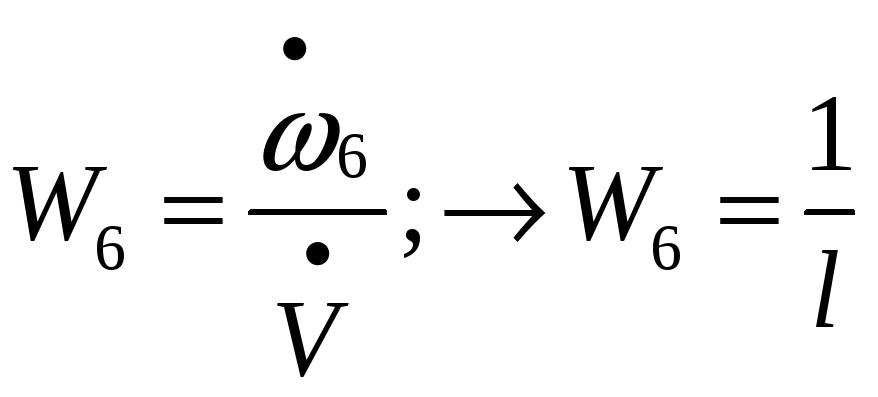
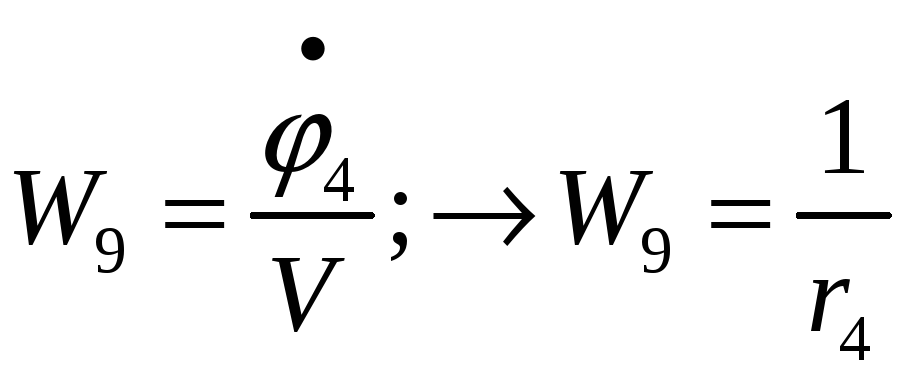
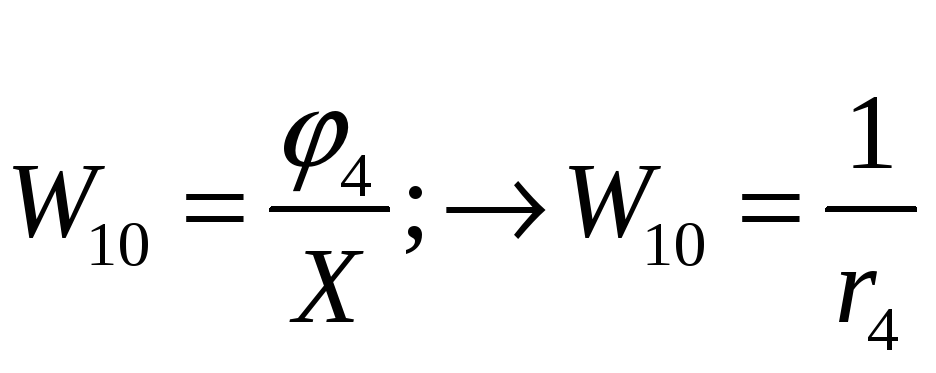
p-оператор Лапласа.

Структурная модель системы:

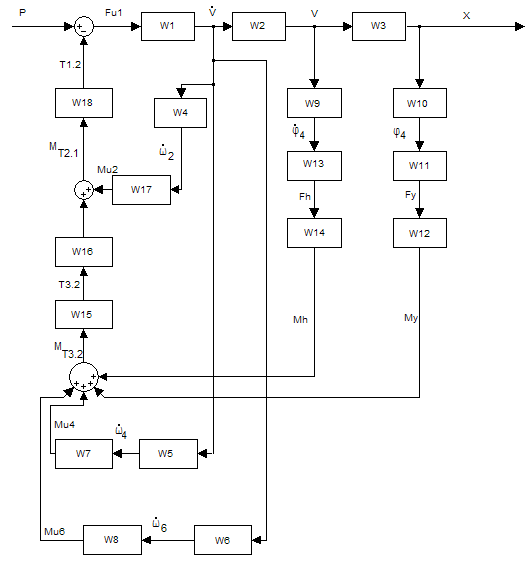
Рис.9. Структурная модель системы.

Построение структурной схемы в MATLAB:

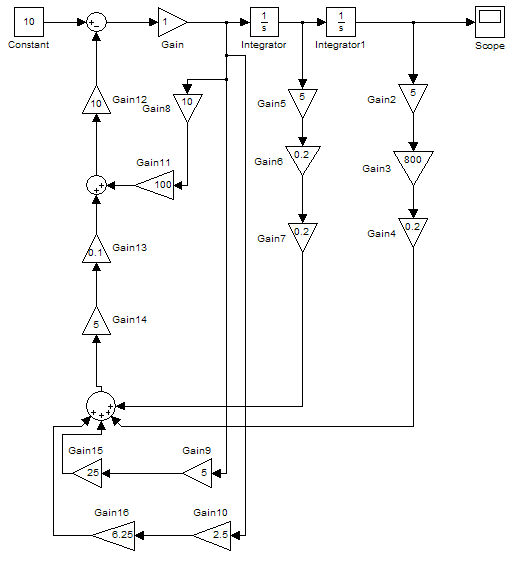
Рис.10. Структурная схема системы.

Графики переходных процессов:

Получаем следующие переходные характеристики движения груза:

Рис.11. Переходной процесс при h = 0 кг/с.

Получаем незатухающие колебания из-за отсутствия сопротивления (коэффициент демпфирования h=0 кг/с).

Исследуем влияние коэффициента демпфирования h. При значении коэффициента демпфирования h=500 кг/с:

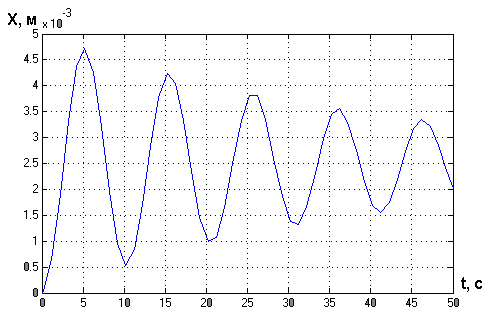
Рис.12. Переходной процесс при h = 500 кг/с.

При увеличении значения коэффициента демпфирования h=7500 кг/с.

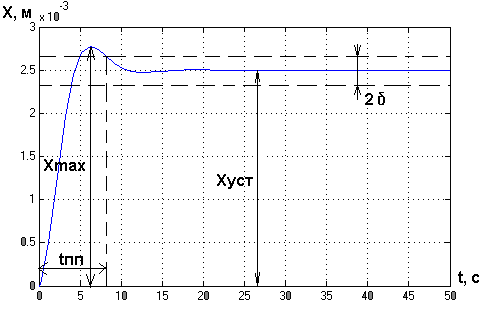
Рис.13. Переходной процесс при h = кг/с.

По полученному графику определим критерии качества.

Максимальное значение перемещения -, установившееся значение - .

Трубка точности (2δ) : , .

Время переходного процесса: t_пп=8 с.

Перерегулирование:

Выводы:

В данной работе мы составили математическую модель объекта на основе законов физики и данной физической модели реального процесса, составив для этого передаточные функции звеньев, которыми связываем значение одних физических величин со значениями других, получившуюся систему смоделировали в MatLab и получили графики колебательных переходных процессов при коэффициенте демпфирования равном 500 кг/с и 7500 кг/с, а затем подобрали его так, чтобы процесс имел лишь одно колебание.

Список литературы.

1) Бессекерский В.А., Попов Е.П. – теория систем автоматического управления / изд. 4-е перераб. И доп. 2004.

2) Чикуров Н. Г. Моделирование технических систем : Учебное пособие / Н. Г. Чикуров; Уфимск. гос. авиац. техн. ун-т; – Уфа: 2005. – 129 с.