45) Соотношение Эйнштейна.

В физике (главным образом в молекулярно кинетической теории) соотношением Эйнштейна (также называемое соотношением Эйнштейна — Смолуховского) называется выражение, связывающее подвижность молекулы (молекулярный параметр) с коэффициентом диффузии и температурой (макро параметры). Оно было независимо открыто Альбертом Эйнштейном в 1905 году и Марианом Смолуховским (1906) в ходе работ по изучению броуновского движения:

где  — коэффициент диффузии,  — подвижность частиц,  — постоянная Больцмана, а

 — абсолютная температура.

Величина подвижности определяется из соотношения

где  — стационарная скорость перемещения частицы в вязкой среде под действием силы .

46) Механизмы рассеяния носителей заряда в неидеальной решетке.

РАССЕЯНИЕ НОСИТЕЛЕЙ ЗАРЯДА в кристаллич. твёрдых телах - процесс взаимодействия электрона проводимости (дырки) с нарушениями идеальной периодичности кристалла, сопровождающийся переходом электрона из состояния с импульсом p в состояние с импульсом . Рассеяние наз. упругим, если энергии электрона в начальном и конечном состояниях равны, или неупругим, если . Источником упругого рассеяния являются статич. дефекты - примесные атомы, дислокации, границы кристаллич. зёрен и т. п. (см. Дефекты в кристаллах). Осн. источником неупругого рассеяния являются колебания кристаллической решётки. Рассеяние электрона на колебаниях решётки описывается в терминах испускания и поглощения фононов движущимся электроном. Особое положение занимает Р. н. з. друг на друге.

При большой плотности носителей рассеяние ослабляется экранированием возмущения из-за перераспределения носителей в пространстве.

Возможно несколько механизмов рассеяния:

на фононах;

на примесях.

47) Взаимодействие носителей заряда с акустическими и оптическими фононами.

Рассеяние на фононах. Вероятность рассеяния электрона при испускании или поглощении фонона о импульсом q и энергией (без учёта принципа Паули) определяется выражением

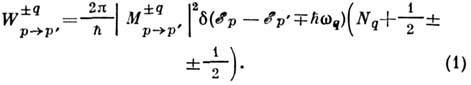
Здесь верх. и ниж. знаки соответствуют испусканию и поглощению фонона; числа фононов с импульсом q определяются распределением Планка (см. Планка закон излучения:)

Матричный элемент М перехода p → p' содержит закон сохранения квазиимпульса: (b - произвольный вектор обратной решётки). Переходы, для к-рых b = 0, наз. нормальными; если b.0, говорят о переходах с перебросом (см. Переброса процессы). Дельта-функция d отражает закон сохранения энергии. Вероятность рассеяния с испусканием фонона пропорц. N_q + 1. Два слагаемых, соответствующие N_q и 1, дают вероятности индуцированного и спонтанного рассеяний. Вероятность рассеяния с поглощением фонона пропорц. N_q, поэтому поглощение фонона всегда является индуцированным.

Рассеяние электрона на фононах в большой степени определяется законами сохранения энергии и импульса (кинематич. факторы), а также принципом Паули. Поэтому картина рассеяния различна для акустич. и оптич. фононов, имеющих разные законы дисперсии , и зависит от степени вырождения электронного газа. Кинематика позволяет установить, какие фононы дают осн. вклад в рассеяние, какова степень упругости рассеяния, а также является ли оно индуцированным или спонтанным.

Рассеяние на акустических фононах в полупроводниках. Т. к. скорость электрона v имеет порядок скорости звука s только при очень малой его энергии ( ! ms² ! 0,1 К), то в реальных условиях Это означает, что возмущение, создаваемое акустич. фононом, почти статично, а рассеяние электронов всегда квазиупруго. Из кинематики следует, что осн. вклад в рассеяние вносят фононы с импульсом ; поэтому

направленный импульс электрона теряется всего за неск. столкновений. Энергия фонона с таким импульсом ! , так что для релаксации энергии требуется много столкновений, т. е. действительно

Является ли рассеяние индуцированным или спонтанным, зависит от соотношения между энергией фонона hsp и тепловой энергией Т. Эти величины сравниваются, когда энергия электрона равна Если то характерны N_q 1; доминирует спонтанное испускание фононов (динамич. трение), и "движение" электрона по оси энергии есть систематич. дрейф вниз. При доминируют индуциров. переходы, т. к. При этом испускание происходит не намного чаще, чем поглощение, и "движение" электрона по оси энергий превращается в диффузию.

Рассеяние на акустических фононах в металлах и вырожденных полупроводниках. Вследствие закона сохранения импульса наиб. вероятно взаимодействие с фононами, импульс к-рых , где - импульс Ферми (см. Ферми-поверхность ).Но испусканию таких фононов (с энергией ) может препятствовать принцип Паули, если превышение энергии электрона над энергией Ферми много меньше , а поглощение может ослабляться из-за малого числа таких фононов, если . Поэтому характер рассеяния сильно зависит от Г и превышения энергии электрона над энергией Ферми. При почти для всех электронов (указанные ограничения несущественны) и рассеяние (с испусканием и поглощением) идёт на фононах с и энергией . Для релаксации импульса требуется неск. столкновений, а для релаксации энергии - много (квазиупругое рассеяние). При поглощение фононов с энергией маловероятно, но если , то принцип Паули не запрещает испускание таких фононов (в осн. спонтанное). Рассеяние, как и при высоких темп-pax, квазиупруго. Если же , то принцип Паули разрешает только испускание фононов с . Такое рассеяние является малоугловым, и выравнивание распределения электронов на поверхности Ферми происходит диффузионно. Для полной релаксации импульса требуется много столкновений, релаксация же энергии происходит за неск. столкновений (неупругое рассеяние).

Рассеяние на оптических фононах. При рассеянии в металлах существенны оптич. фононы во всей зоне Бриллюэна, в осн. коротковолновые с , где b₀ - размер Бриллюэна зоны. В полупроводниках в рассеянии участвуют только оптич. ДВ-фононы с . Частоту этих фононов w₀ можно считать не зависящей от q. Рассеяние на оптич. фононах квазиупруго только при ! 400 К, т. е. только при очень высоких энергиях электронов (см. Горячие электроны ).В области энергий проявляются неупругий и пороговый характеры рассеяния. Это существенно при низких темп-pax , когда ниже порога ( ) рассеяние слабое и возможно только за счёт маловероятного поглощения фонона, пропорционального , а выше порога ( ) рассеяние сильное - оно происходит при спонтанном испускании фонона.