
- •Содержание
- •Введение
- •Лабораторная работа 1 Дискретные распределения
- •Краткие теоретические сведения
- •Биноминальное распределение и игровые задачи
- •Задача шевалье де Мере
- •Распределение редких событий (Пуассона)
- •Задания для выполнения
- •Лабораторная работа 2 Основные модели теоретических распределений (Statistica 6)
- •Краткие теоретические сведения
- •Вероятностный калькулятор
- •Нормальное распределение
- •Правила 2 и 3 сигма
- •Логарифмически-нормальное распределение
- •Задания для выполнения
- •Лабораторная работа 3 Распределение параметров выборки
- •Краткие теоретические сведения
- •Распределение χ-квадрат (хи-квадрат)
- •Задания для выполнения
- •Лабораторная работа 4 Разнообразие значений признака (ms Excel)
- •Краткие теоретические сведения
- •Подготовительные процедуры
- •Первичный анализ статистических данных
- •Проверка на условие нормальности распределения
- •Гистограмма
- •Первичный анализ статистических данных
- •Задания для выполнения
- •Лабораторная работа 6 Парная корреляция (ms Excel)
- •Краткие теоретические сведения
- •Корреляционный анализ
- •Регрессионный анализ
- •Задания для выполнения
- •Лабораторная работа 8 Частная и множественная линейные корреляции и регрессия (Statistica 6)
- •Краткие теоретические сведения
- •Описание модели
- •Постановка задачи
- •Задания для выполнения
- •Лабораторная работа 9 Криволинейная корреляция и регрессия (ms Excel)
- •Краткие теоретические сведения
- •Проведение анализа
- •Задания для выполнения
- •Лабораторная работа 11 Однофакторный дисперсионный анализ (однофакторный комплекс в ms Excel)
- •Краткие теоретические сведения
- •Проведение анализа
- •Задания для выполнения
- •Лабораторная работа 13 Многофакторный дисперсионный анализ (двухфакторный комплекс в ms Excel)
- •Краткие теоретические сведения
- •Проведение анализа
- •Задания для выполнения
- •Лабораторная работа 15 Классификация (дискриминантный анализ в Statistica 6)
- •Краткие теоретические сведения
- •Классификация цветов ириса
- •Задания для выполнения
- •Лабораторная работа 16 Классификация (кластерный анализ в Statistica 6)
- •Краткие теоретические сведения
- •Кластеризация автомобилей в модуле Cluster Analysis (Кластерный анализ)
- •Классификация населенных пунктов, расположенных в зоне радиоактивного загрязнения
- •Задания для выполнения
- •Литература
- •Приложение а (обязательное)
- •Приложение б (обязательное)
- •Приложение в (обязательное)
- •Приложение г (обязательное)
- •Приложение д (обязательное)
- •Приложение е (обязательное)
- •Приложение ж (обязательное)
- •Приложение и (обязательное)
Лабораторная работа 3 Распределение параметров выборки
Цель работы: научиться работе с вероятностным калькулятором в программном продукте Statistica 6 на примерах распределений: F-распределение Фишера, t-распределение Стьюдента и распределение χ-квадрат.
Краткие теоретические сведения
F-распределение возникает в регрессионном, дисперсионном и дискриминантном анализе, а также в других видах многомерного анализа данных. Далее оно будет неоднократно встречаться в таблицах вывода системы Statistica 6.
Случайная величина, имеющая F-распределение с парой степеней свободы m, n, определяется как отношение двух независимых случайных величин, имеющих распределение χ-квадрат (хи-квадрат) со степенями свободы m и n с умножением на нормировочный сомножитель n/m.
F-распределение сосредоточено на положительной полуоси. Это распределение в отличие от нормального несимметрично. Покажем, как построить график F-распределения и вычислить его процентные точки.
t-распределение важно в тех случаях, когда рассматриваются оценки среднего и неизвестна дисперсия выборки. В этом случае используют выборочную дисперсию и t-распределение.
t-распределение возникает в таблицах вывода регрессионного анализа. Это одно из важнейших распределений, наряду с нормальным и распределением χ-квадрат (хи-квадрат).
t-распределение с k-степенями свободы сосредоточено на всей действительной оси, симметрично относительно нуля. Среднее t-распределения равно нулю, дисперсия равна k/(k-2).
Случайная величина, имеющая распределение χ-квадрат, определяется как сумма квадратов k независимых стандартных нормальных величин. Нормальные случайные величины – это величины, имеющие нормальное распределение. Число k в определении χ-квадрата называется числом степеней свободы. В частном случае, когда k = l случайная величина χ-квадрат равна квадрату стандартной нормальной величины. Итак, это распределение имеет только один параметр – число степеней свободы, являющийся целым положительным числом.
F-распределение Фишера
В списке распределений вероятностного калькулятора выберите F (Fisher) (F-распределение) (рисунок 3.1 а).
Задайте в поле df1 (степень свободы 1) значение 10, в поле df2 (степень свободы 2) — значение 11. Пометьте опцию Create Graph (Создать график).
В поле р задайте 0,5. Нажав кнопку Compute (Вычислить), на экране вы увидите следующий график (рисунок 3.1 б).


а) б)
Рисунок 3.1 – F-распределение в вероятностном калькуляторе: а) задание; б) плотность и функция F-распределения со степенями свободы 10, 11
t-распределение Стьюдента
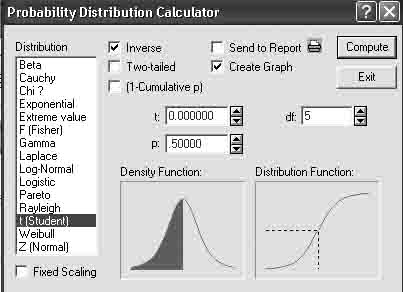
В списке распределений вероятностного калькулятора выберите t (Student) (t-распределение Стьюдента) (рисунок 3.2 а).
В строке df задайте 5 – число степеней свободы. Пометьте опцию Create Graph (Создать график).
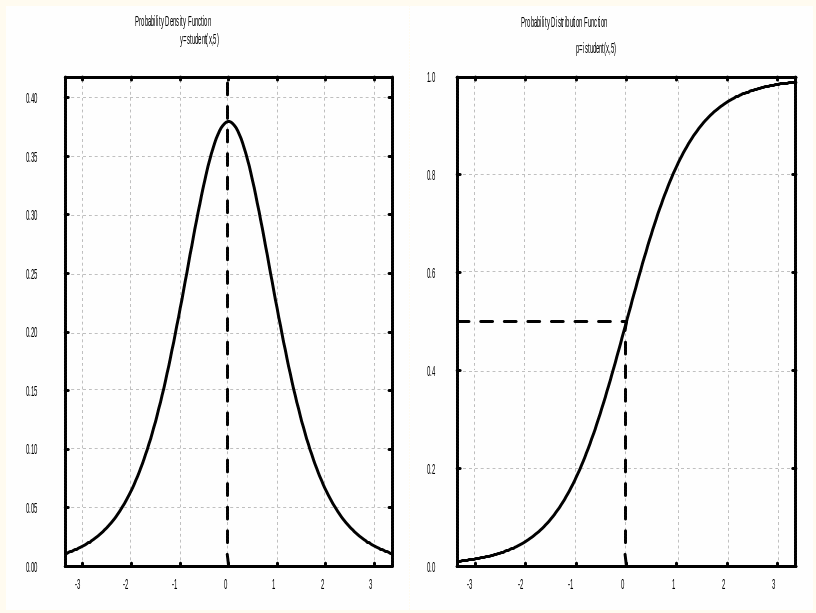
В поле р задайте 0,5. Нажмите кнопку Compute (Вычислить), на экране вы увидите следующий график (рисунок 3.2 б).
При больших степенях свободы (больших 30) t-распределение практически совпадает со стандартным нормальным распределением.
Плотность t-распределения деформируется при возрастании числа степеней свободы следующим образом: пик увеличивается, хвосты более круто идут к нулю, кажется, как будто плотность сжимается с боков.
a) б)
Рисунок 3.2 – t-распределения Стьюдента в вероятностном калькуляторе: a) задание; б) плотность и функция t-распределения Стьюдента с 5 степенями свободы
В такой деформации плотности легко убедиться с помощью вероятностного калькулятора. Задайте в поле df (степень свободы) значение 50. Нажав кнопку Compute (Вычислить), на экране вы увидите следующий график (рисунок 3.3).
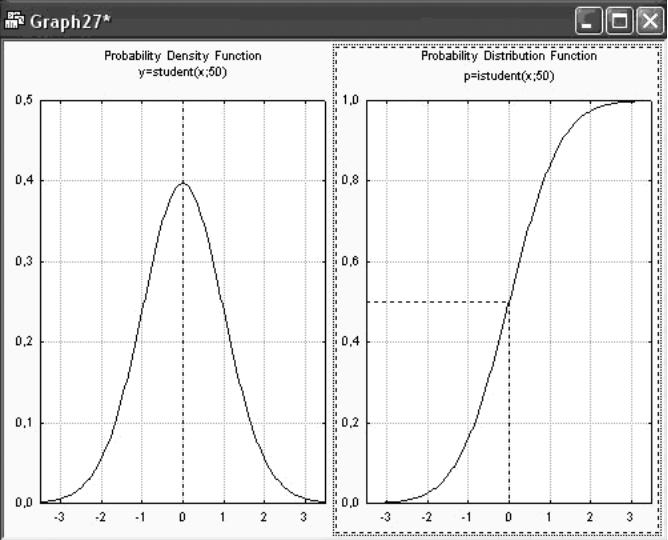
Рисунок 3.3 – Плотность и функция распределения Стьюдента с 50 степенями свободы
Сравнив график плотности распределения Стьюдента с большим числом степеней свободы, например 50, и график плотности стандартного нормального распределения, вы убедитесь, что они очень похожи.
