Правила 2 и 3 сигма
Правила 2 и 3 сигма полезно знать. Они часто используются на практике. Смысл этих правил состоит в том, что если от точки среднего или от точки максимума плотности нормального распределения отложить вправо и влево соответственно два и три стандартных отклонения (2 и 3 сигма), то площадь под графиком нормальной плотности, подсчитанная по этому промежутку, будет соответственно равна 95,45% и 99,73% всей площади под графиком.
Другими словами, это можно выразить следующим образом: 95,45% и 99,73% всех независимых наблюдений из нормального распределения лежат в пределах двух и трех стандартных отклонений от среднего значения.
Это правило также легко проверить с помощью вероятностного калькулятора. Выберите нормальное распределение в списке распределений, задайте, например, стандартные параметры: среднее = 0, стандартное отклонение = 1, пометьте опцию Two-tailed (Двухсторонний), в строке X задайте 2 (два стандартных отклонения), нажмите Compute, в строке р появится значение 0,9545 (рисунок 2.6).
В поле Density Function (Функция плотности) вероятностного калькулятора показана заштрихованная площадь под графиком плотности, в поле р показано значение 0,9545. Переходя к процентам, имеем 95,45%. Заштрихованная площадь составляет 95,45% всей площади под графиком.
Рисунок 2.6 – Иллюстрация к правилу 2 сигм
Выберите нормальное распределение, задайте стандартные параметры: среднее = 0, стандартное отклонение = 1, пометьте опцию Two-tailed в строке X задайте 3 (три стандартных отклонения), нажмите Compute, в строке р появится значение 0,9973 (рисунок 2.7).
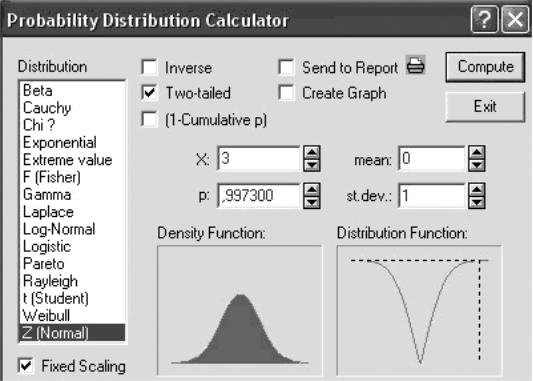
Рисунок 2.7 – Иллюстрация к правилу 3 сигм
Данные правила действуют при любых значениях среднего и стандартного отклонения нормального закона.
Логарифмически-нормальное распределение
Плотность распределения имеет одно максимальное значение и несимметрично. График плотности логарифмически-нормального распределения показан на рисунке 2.8 а.
В списке распределений вероятностного калькулятора выберите Log-Normal (Логнормальное распределение), рисунок 2.8 б).
а) б)
Рисунок 2.8 – Логарифмически-нормальное распределение в вероятностном калькуляторе: а) задание; б) плотность распределения
Задания для выполнения
С помощью вероятностного калькулятора вычислите вероятности при заданном среднем и стандартном отклонении (таблица 2.1).
Дайте объяснение полученным результатам.
Таблица 2.1 – Задание для выполнения расчетов
№ варианта |
Среднее |
Стандартное отклонение |
Минимум |
Максимум |
1 |
10 |
8 |
8 |
12 |
2 |
10 |
5 |
8 |
12 |
3 |
10 |
3 |
8 |
12 |
4 |
10 |
1 |
8 |
12 |
5 |
10 |
0,5 |
8 |
12 |
6 |
20 |
5 |
8 |
12 |
7 |
15 |
5 |
8 |
12 |
8 |
10 |
5 |
8 |
12 |
9 |
5 |
5 |
8 |
12 |
10 |
1 |
5 |
8 |
12 |