3. Геометрические приложения определенных интегралов.

   Если на отрезке          функция         , то площадь криволинейной трапеции, ограниченной кривой         , осью          и прямыми          (рис. 9), равна 

        Если          на отрезке         , то площадь соответствующей криволинейной трапеции 

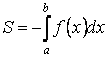
Рисунок 9.

        В общем случае, когда функция          меняет знак на отрезке          (рис. 10), площадь, ограниченная кривой         , осью          и прямыми          может быть найдена как сумма площадей фигур, лежащих выше и ниже оси         . Иначе 

Рисунок 10.

        Длина дуги кривой         , ограниченной точками с абсциссами          , вычисляется по формуле 

        Рассмотрим тело, образованное вращением вокруг оси          криволинейной трапеции, ограниченной кривой         , осью          и прямыми          . Объём тела вращения 

        Пусть кривая задана уравнениями в параметрической форме 

,

где          и          . Площадь криволинейной трапеции в этом случае равна 

а длина дуги 

3. 

        Пусть кривая задана уравнением в полярной системе координат 

,

где          - непрерывная функция, определённая при          (рис. 11). Площадь сектора, ограниченного заданной кривой и лучами          ,          , равна 

  Рисунок 11.

        Длина дуги кривой, определённой в полярной системе координат уравнением         , вычисляется по формуле 

3. Вычисление плоских фигур.

4. Функции многих переменных: определение. Область определения и область значения

5. Предел функции в точке, повторные пределы. Непрерывность функции в точке

6. Частные производные. Полный дифференциал.

7. Производная сложной функции.

8. Производная по направлению.

9. Градиент.

10. Частные производные высших порядков.

11. Экстремум функции многих переменных (при п=2) условный экстремум.

12. Определение двойного интеграла и его свойства.

13. Сведение двойного интеграла к повторному. Изменение порядка интегрирования.

14. Вычисление двойного интеграла в полярной системе координат.