2. Двуосное напряженное состояние.

Нормальные напряжения возникают в направлении как оси , так и .

Рис. 20. Напряжения при двухосном состоянии

Рассмотрим равновесие трехгранного элемента. Пусть – площадь грани, перпендикулярной (на ней напряжение равно ).

На грани, перпендикулярной , , площадь наклонной грани . На грань действует сила , на грань – сила . Проецируя силы на направление нормали к площадке:

,

. (1)

Проецируя на направление :

,

. (2)

Формулы (1,2) дают полное решение задачи.

3. Плоское напряженное состояние.

Кроме нормальных, есть и касательные напряжения. Показано положительное направление .

Рис. 21. Напряжения при плоском состоянии

Условия равновесия трехгранника дают:

;

.

Из тригонометрии:

; ;

.

Получим формулы:

;

.

Такие же формулы выполняются для двуосного состояния, при .

Правила знаков для напряжений:

а) все нормальные напряжения положительны при растяжении;

б) касательное напряжение положительно, если напряжение по оси ;

в) касательное напряжение положительно, если направлено по часовой стрелке (см. рис. 21).

4. Главные напряжения.

Экстремум как функции : :

.

Для угла получим .

Получим два значения , которые соответствуют минимуму и максимуму .

Главные напряжения:

.

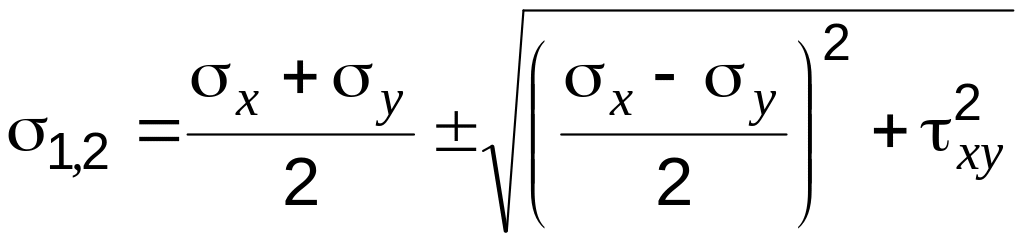5. Круг Мора для двуосного напряженного состояния

Обозначим , .

Можно найти: , .

Это уравнение окружности с параметром .

Из них следует: – уравнение окружности радиусом и с центром в точке , изображенной на рис. 22.

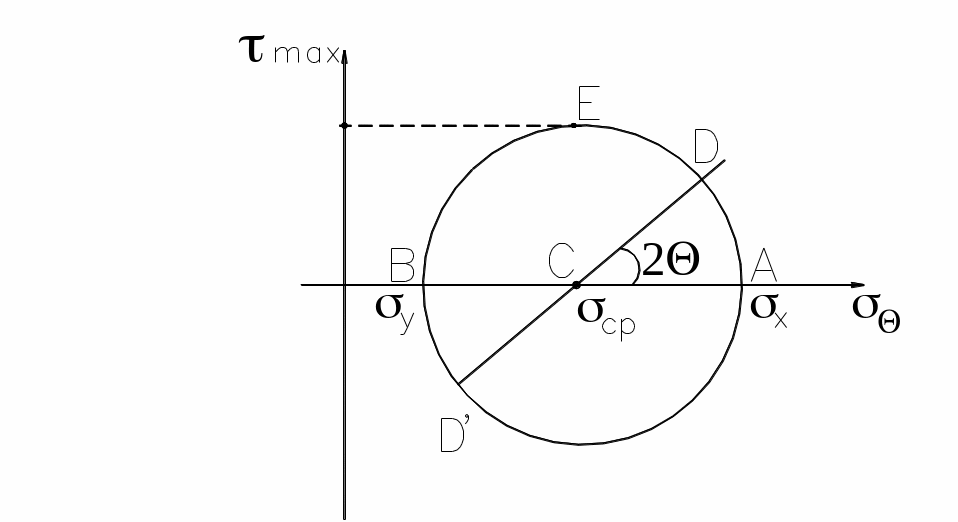
Рис. 22. Круг Мора

Координаты точки – напряжения , на плоскости под углом .

– точка максимального касательного напряжения.

Параллельно угол измеряется от точки , определенной величиной .

При , левее точки .

Пример. Построить круг Мора для двуосного напряженного состояния при , . Определить , для .

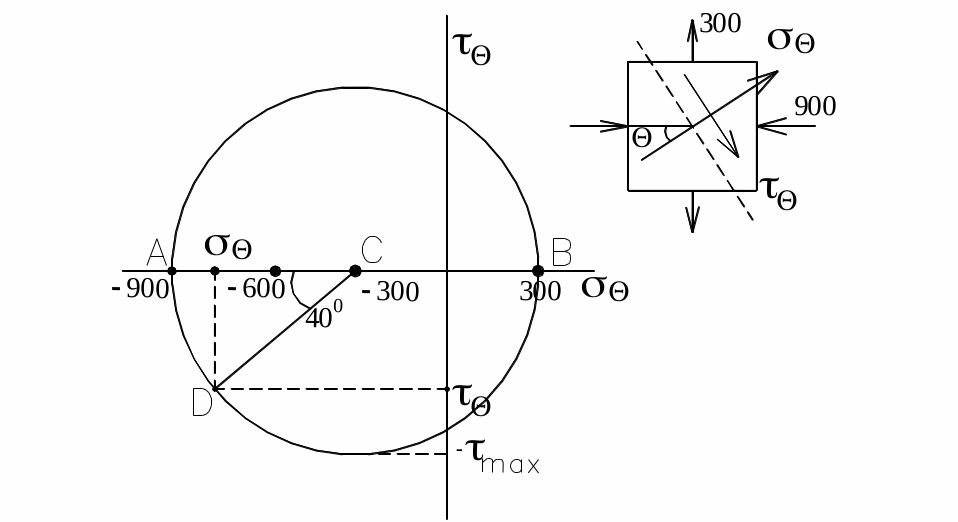
Рис. 23. Построение круга Мора

РЕШЕНИЕ.

– координаты центра круга.

Радиус круга .

Откладывая угол против часовой стрелки от точки , получим точку с координатами: ; .

2. Круг Мора для плоского напряженного состояния

Соотношения

для напряжений на площадке под углом к оси преобразуем заменой :

Получим уравнение окружности с центром , :

.

Алгоритм построения круга Мора:

1. Определить центр круга, координаты , .

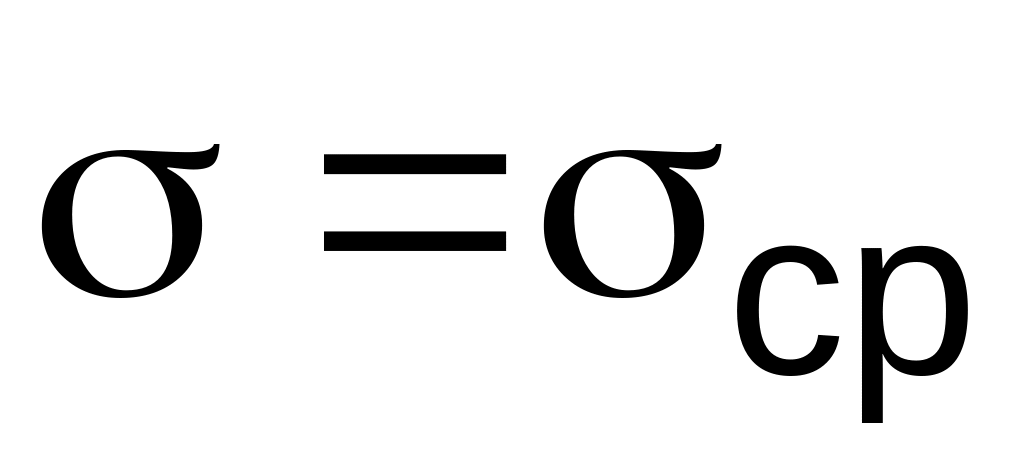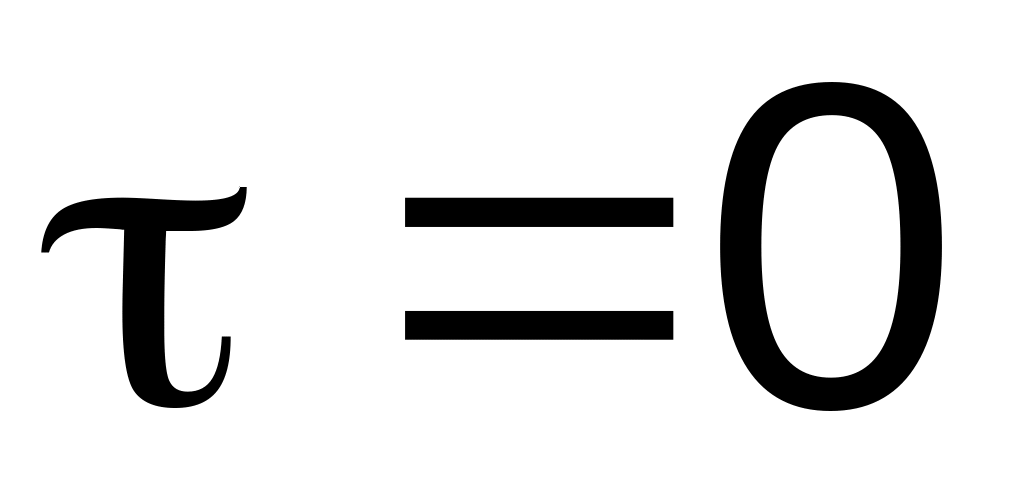2. Положение точки : 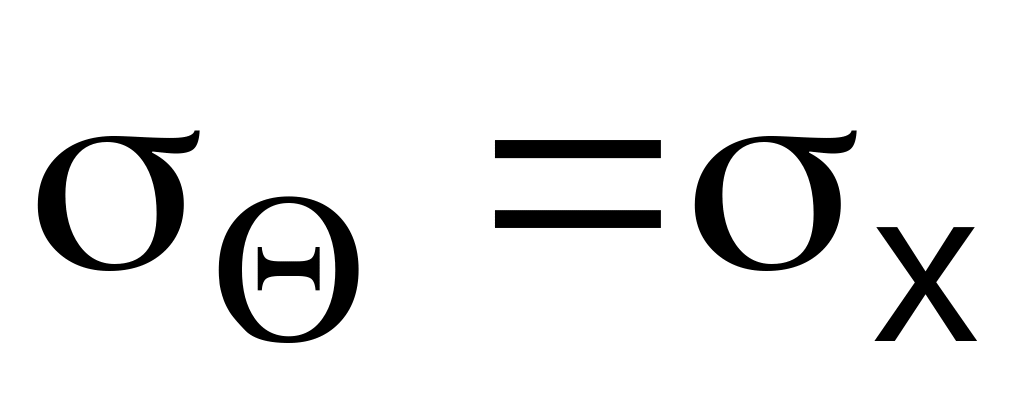, 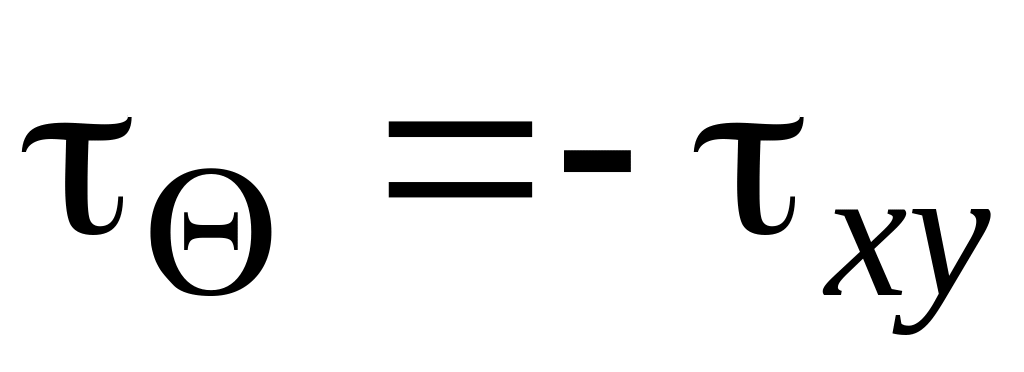(в соответствии с правилом знаков, противоположно . Координаты точки : 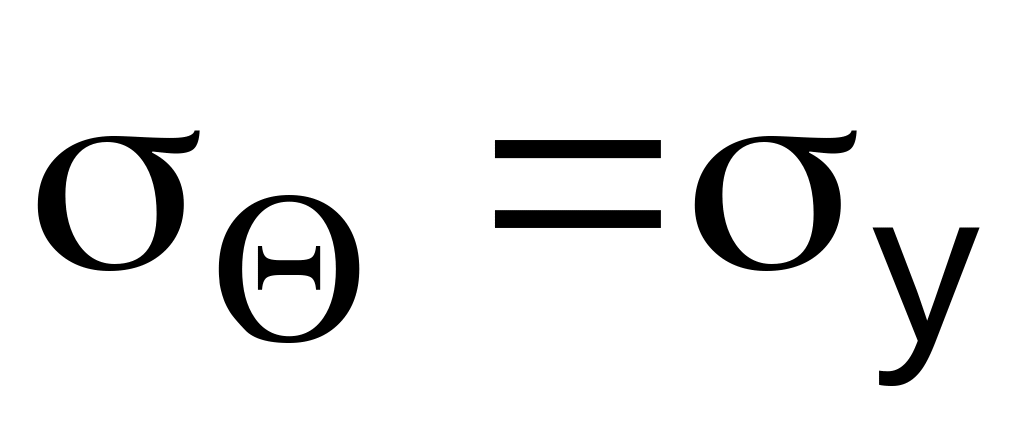, 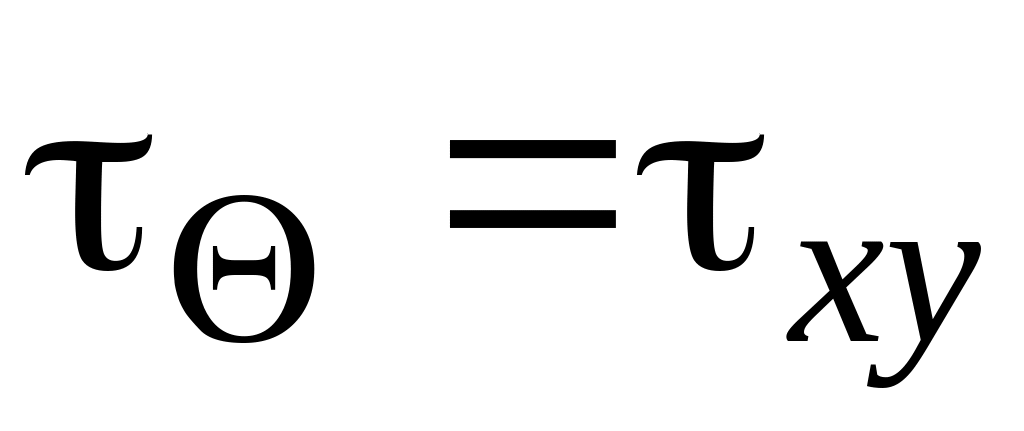. Точки , , должны лежать на одной прямой.

3. Круг диаметром и центром .

4. Для определения напряжения на наклонной плоскости с нормалью под углом к отложить против часовой стрелки от точки .

2. Деформация при двуосном напряженном состоянии

а) эффект Пуассона: осевое удлинение сопровождается уменьшением поперечного размера:

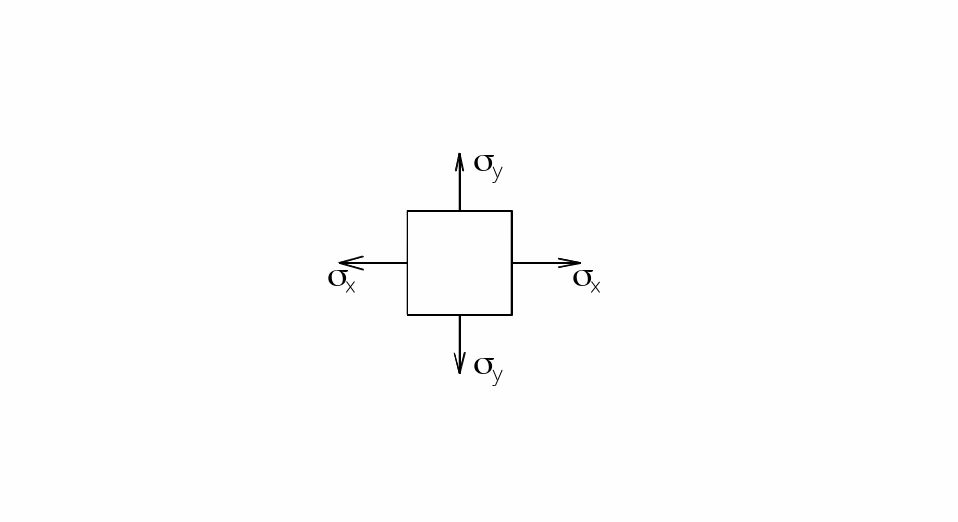
Рис. 24. Напряжения при двухосном состоянии

.

б) деформация вдоль зависит от . При выполнении закона Гука:

аналогично:

от ; от – величины деформации.

Деформация в направлении :

Обратно, выполняются:

в) изменение объема стержня:

– изменение размера элемента в направлении. Объем увеличится в отношении: или, если обратить малые величины порядков:

Тогда относительное изменение объема:

Выразим деформации через напряжения:

Материал этой главы можно подробнее изучить по учебнику [6].