
- •Специальные главы механики деформируемых тел
- •Введение
- •Глава 1. Деформации и напряжения в тонкой пластине
- •Основные понятия и гипотезы
- •Перемещения и деформации в пластинке
- •Напряжения в пластинке
- •Усилия в тонкой пластинке
- •5. Вывод уравнений равновесия пластинки
- •Глава 2. Уравнения равновесия тонкой пластины
- •Формулировка граничных условий
- •Изгиб круглой пластинки
- •Глава 3. Равновесие прямоугольной пластины
- •Глава 4. Прочность пластин. Применение вариационных принципов к расчету пластин
- •Энергия тонкой пластинки
- •2. Критерий прочности тонкой пластинки
- •3. Деформационный критерий несущей способности пластин
- •4. Вариационные принципы при расчете пластин
- •5. Пример расчета пластинки с использованием принципа минимума энергии деформации
- •Глава 5. Сложное напряженное состояние деформируемых тел
- •1. Свободная энергия стержня в общем случае нагружения
- •2. Теорема Кастилиано
- •3. Интеграл Мора
- •Глава 6. Упругопластическое кручение и изгиб стержня
- •Условия пластичности. Состояние пластичности
- •Идеальная пластичность
- •Упругопластический изгиб призматического бруса
- •Упругопластическое кручение круглого бруса
- •Кручение некруглых стержней
- •Глава 7. Исследование напряженного состояния
- •Напряжения в наклонном сечении при растяжении (одноосное напряженное состояние).
- •Двуосное напряженное состояние.
- •Плоское напряженное состояние.
- •4. Главные напряжения.
- •5. Круг Мора для двуосного напряженного состояния
- •Круг Мора для плоского напряженного состояния
- •Деформация при двуосном напряженном состоянии
- •Глава 8. Основы механики разрушения
- •1. История и литература. Исходная задача об эллиптическом отверстии.
- •2. Энергия деформации пластинки с отверстием и коэффициент интенсивности напряжений
- •3. Критическое равновесие трещины
- •4. Схема расчета на трещиностойкость
- •5. Учет пластической зоны
- •6. Учет конечности размеров пластины
- •7. Экспериментальное определение коэффициента интенсивности напряжений
- •Заключение
- •Рекомендуемый библиографический список
- •Содержание
- •Специальные главы механики деформируемых тел
- •680021, Г. Хабаровск, ул. Серышева, 47.
Упругопластическое кручение круглого бруса
Предполагая, что поперечные сечения остаются плоскими и за пределами упругости, получим для касательных напряжений
![]() ,
,
![]() – расстояние от центра.
– расстояние от центра.
Тогда
![]()
![]()
Из условия Губера-Мизеса-Генки
![]() .
.
Определение.
Величина
![]() в случае кручения называется пределом
текучести при сдвиге.
в случае кручения называется пределом
текучести при сдвиге.
Условие пластичности:
,
так
как
![]() по определению.
по определению.
Зависимость напряжений от расстояния до оси при идеальной пластичности:
![]()
 при
при
![]()
при
![]() .
.
![]() – радиус
упругого ядра.
– радиус
упругого ядра.
Зная , можно из условия
![]() найти
.
найти
.
Эпюра напряжений изображена на рис. 18.

Рис. 18. Напряжения в брусе при кручении
Два
предельных состояния: предел упругого
деформирования, когда
![]() ;
предел пластического деформирования,
;
предел пластического деформирования,
![]() .
.
![]() – предельный
момент, все сечение в пластическом
состоянии.
– предельный
момент, все сечение в пластическом
состоянии.
Получим
формулу для
![]() .
Касательные напряжения не зависят от
и уравновешивают внешний момент
:
.
Касательные напряжения не зависят от
и уравновешивают внешний момент
:
![]() .
.
Пусть
![]() – площадь упругой и пластической зон.
– площадь упругой и пластической зон.
![]()
Интегралы
равны
![]()
 ;
;
 ;
;
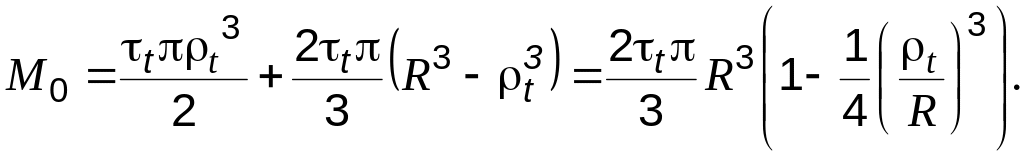
При , т. е. когда весь стержень в пластическом состоянии:
![]() .
.
Кручение некруглых стержней
Рассмотрим
тонкий прямой стержень любого сечения.
Ось
направим вдоль стержня через центр
тяжести сечения. Определим угол
кручения
![]() как угол поворота, отнесенный к единице
длины, т. е. если два бесконечно близких
сечения поворачиваются на угол
как угол поворота, отнесенный к единице
длины, т. е. если два бесконечно близких
сечения поворачиваются на угол
![]() ,
то
,
то
![]() .
.
Деформации
малы, но угол
![]() может быть большим.
может быть большим.
При
повороте сечения на угол
![]() смещение конца радиус-вектора точки
определяются по формуле
смещение конца радиус-вектора точки
определяются по формуле
![]() .
(1)
.
(1)
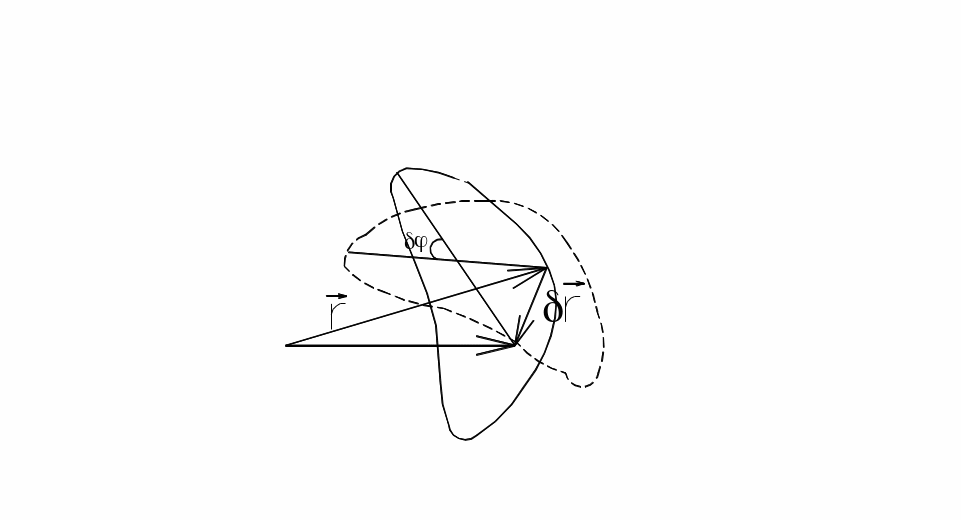
Рис. 19. Поворот сечения и изменение радиус-вектора
![]() – вектор,
направленный вдоль
и
– вектор,
направленный вдоль
и
![]() .
.
Для точек с координатой
![]() .
(2)
.
(2)
Тогда перемещения точек равны из (1):
![]() ,
,
![]() .
(3)
.
(3)
Для малых деформаций можно считать, что смещение точек вдоль пропорционально
![]() .
(4)
.
(4)
![]() – функция
кручения.
– функция
кручения.
То есть каждое сечение поворачивается вокруг , искривляясь.
Зная перемещения, из соотношений Коши найдем деформации:
![]() ;
;
![]() ;
;
![]() .
.
Из закона Гука напряжения равны:
![]() ;
;


Отсюда получим уравнение равновесия:
![]()
или
![]() ,
так как
,
так как
![]() .
.
Для
полного решения задачи надо найти
и угол кручения
.
В наиболее типичном случае к концам
стержня приложены равные и противоположно
направленные моменты
![]() .
При этом
.
При этом
![]() и
~
.
Обычно принимают соотношение
и
~
.
Обычно принимают соотношение
![]() ,
где
,
где
![]() называется крутильной жесткостью
стержня.
называется крутильной жесткостью
стержня.
Для круглого стержня:
![]() .
.
Для
эллиптического стержня с полуосями
![]() :
:
![]() .
.
Для
стержня в виде длинной тонкой пластинки
(ширина
![]() ,
толщина
,
толщина
![]() ):
):
![]() .
.
Дополнительные формулы и определения:
![]()
![]() ;
;
![]() ;
;
![]() на
контуре сечения (односвязном!).
на
контуре сечения (односвязном!).
![]() – жесткость.
– жесткость.
![]() – свободная
энергия.
– свободная
энергия.
Глава 7. Исследование напряженного состояния
Напряжения в наклонном сечении при растяжении (одноосное напряженное состояние).
а
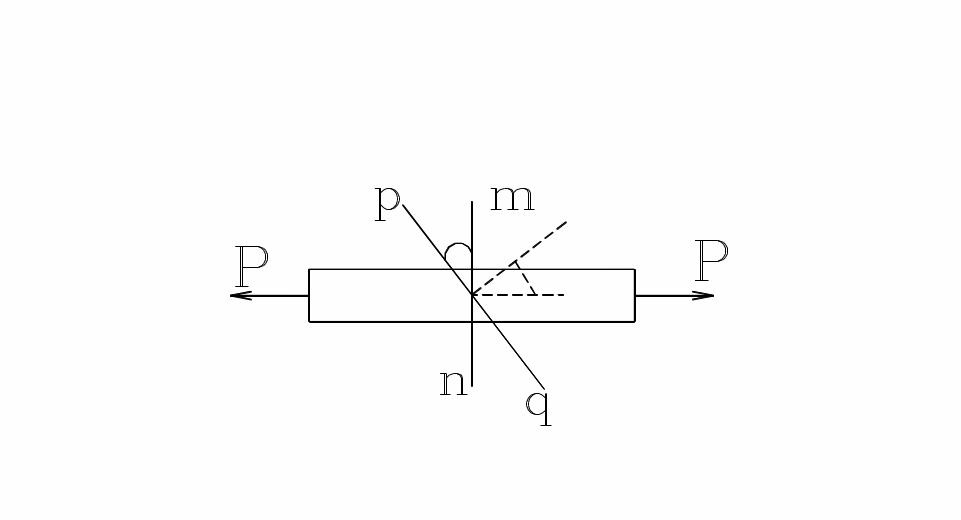
б

Рис. 19. Площадки и силовые факторы
В
сечении (mn)
![]() ,
где
,
где
![]() – сила,
– сила,
![]() – площадь. При этом
– площадь. При этом
![]() – главное напряжение.
– главное напряжение.
Пусть
сечение (pq)
под углом
к (mn).
Равнодействующая сил
![]() ,
распределенных по (pq),
равна
,
так как стержень в равновесии. площадь
(pq)
равна
,
распределенных по (pq),
равна
,
так как стержень в равновесии. площадь
(pq)
равна
![]() .
Силу
разложим на нормальную
.
Силу
разложим на нормальную
![]() и касательную
и касательную
![]() :
:
![]() ,
,
![]() .
.
Напряжения по определению равны:
![]()
![]() .
.
При
![]() нормальное напряжение максимально:
нормальное напряжение максимально:
![]() .
.
При
![]() касательное напряжение максимально:
касательное напряжение максимально:
![]() .
.
