5. Вывод уравнений равновесия пластинки

Рассмотрим элемент пластинки . Все усилия надо умножать на длину грани, чтобы получить силу.

Рис. 4. К выводу уравнений равновесия

Спроецируем силы на :

,

где – нагрузка на единицу площади. Получим:

Уравнение моментов всех сил относительно :

.

Отсюда получим (пренебрегая вторыми порядками):

.

Аналогично из уравнения моментов относительно :

Исключая из уравнений , , получим:

Подставив сюда выражения для моментов (5), (6) и приведя подобные, получим:

(7)

Обычно его записывают в виде:

, где

– оператор Лапласа.

Это – основные уравнения изгиба пластинки. В его решение входят произвольные функции, определяемые из краевых условий закрепления.

Глава 2. Уравнения равновесия тонкой пластины

1. Формулировка граничных условий

Рассмотрим прямоугольную пластинку (рис. 5).

Рис. 5. Координаты и размеры пластинки

1. Защемленный край: нет ни прогибов, ни поворотов:

при , : ;

при , : .

2. Шарнирно опертый край:

при : ;

Выразим момент через : .

Однако при , тождественно , поэтому для шарнирно опертой пластинки:

при , : .

Аналогично получим:

при , : .

Определение. Дифференциальное уравнение в частных производных с заданными на границе области соотношениями для искомых функций называется краевой задачей.

2. Изгиб круглой пластинки

В полярных координатах оператор Лапласа имеет вид:

.

Уравнение изгиба инвариантно относительно координат:

.

В полярных координатах:

.

Пусть нагрузка на пластинку и условия закрепления не зависят от координаты . Тогда уравнение имеет вид;

. (*)

Изгибающие моменты при этих условиях равны:

;

, (1)

а крутящий момент обращается в нуль.

Для свободно опертой по краю пластинки краевые условия будут:

, , при . (**)

Прямой подстановкой можно проверить, что функция:

(2)

является общим решением (*) при .

Из (**) можно найти значения произвольных постоянных :

при :

.

Отсюда для прогибов получим:

. (3)

Максимальный прогиб, очевидно, в центре пластинки при :

.

Подставляя в формулу (1) для моментов, получим:

,

.

Это – параболические функции.

Максимальные моменты – также в центре:

.

Аналогично из краевых условий

можно из (2) найти и из (1) – для защемленной по краю пластины.

Глава 3. Равновесие прямоугольной пластины

Рис. 6. Геометрия задачи и краевые условия

Рассмотрим шарнирно опертую по краю пластинку. Для нее краевая задача имеет вид:

при (1)

при

Решение ищем в виде двойного тригонометрического ряда:

Обычно применяют сокращенную запись:

Задача сводится к определению коэффициентов Ряд (2) удовлетворяет краевым условиям в силу того, что .

Для определения надо разложить нагрузку q(x,y) в ряд, аналогичный (2), найти производные от w, подставить все эти данные в уравнение (1) и сравнить эти коэффициенты при одинаковых тригонометрических функциях слева и справа. Сделаем это:

где известно из курса математического анализа.

Собирая все результаты, получим:

(3)

Сравнивая левую и правую части, получим:

, откуда

Таким образом, функция (2) полностью определена. Частные случаи:

1. нагрузка равномерно распределена по поверхности, q = const:

          при нечетных m = 1, 3, 5..; n = 1,3,5…(при четных ).

Подставляя в решение (2), получим:

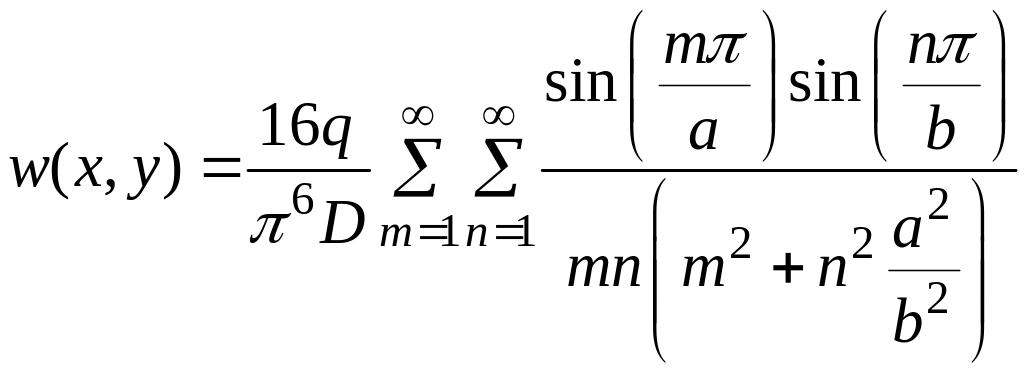, (m, n = 1,3,5,..) (4)

Моменты выражаются через прогибы по формулам:

Вторые производные равны:

.

Подставляя в формулы для моментов, получим:

Максимальные изгибающие моменты возникают в центре пластины при . Для составления таблиц их представляют в виде:

, где – функции отношения . Ряд (5) сходится медленнее, чем (4), так как степень числителя выше.

Эпюры изгибающих моментов получаются табулированием функций (5). Для их построения надо оставить 4 слагаемых в ряде, т. е. члены для значений m = 1;3, n = 1;3 и протабулировать (5) с шагом hx по x, hy по y. Ошибка при этом не превышает 3 % от точного значения.

2. сила Р сосредоточена в точке К с координатами x₀, y₀. Тогда, используя -функцию, получим:

Тогда для прогибов получим:

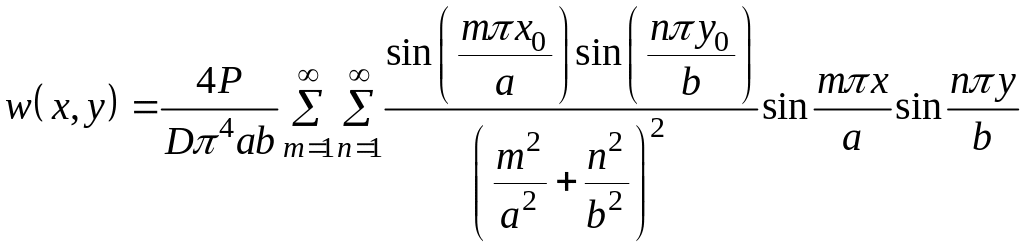
Этот ряд сходиться медленно, ряды же для М_х и М_у сходятся еще медленнее. Поэтому эту методику можно использовать в данном случае только для нахождения прогибов. После определения можно на компьютере численно найти и построить эпюры M_x, M_y.