3. Критическое равновесие трещины

Для продвижения трещины на длину dl (см. рис. 27) должны быть разрушены внутренние связи в материале пластины. Гриффитс предложил выразить работу по их разрушению в виде:

, где – площадь поверхности при единичной ширине, – константа материала; коэффициент 2 – потому что два берега трещины.

В общем случае 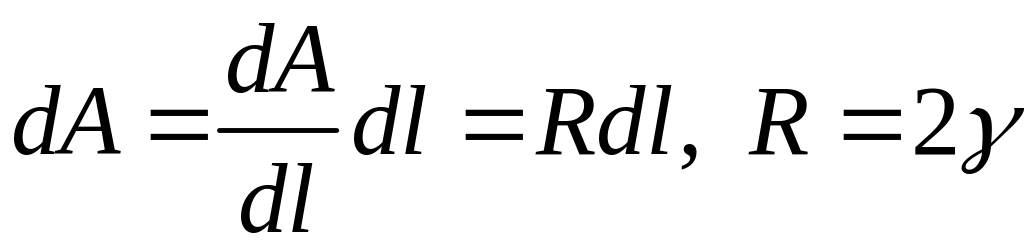, где R – сопротивление росту трещины.

С другой стороны, по закону сохранения энергии dA = –dU, откуда или, учитывая исправленное выражение для из (4):

, (5)

где R – константа материала, равная 2 .

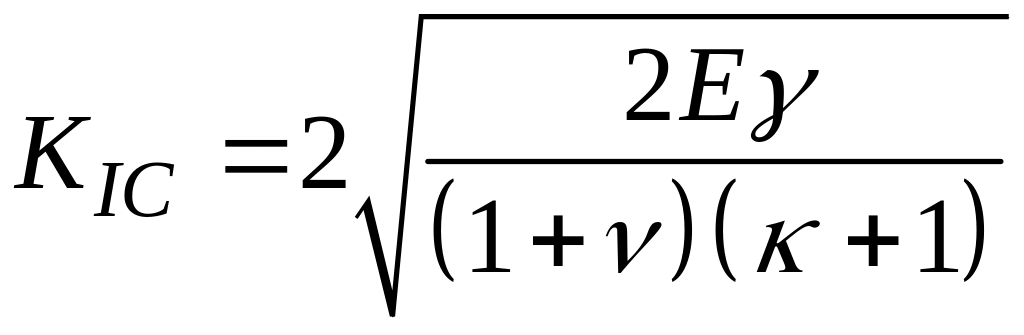Равенство называют энергетическим критерием роста трещины. С другой стороны, величину называют критическим коэффициентом интенсивности напряжений, а равенство – силовым критерием роста трещины.

Поскольку напряжения при выражается формулой 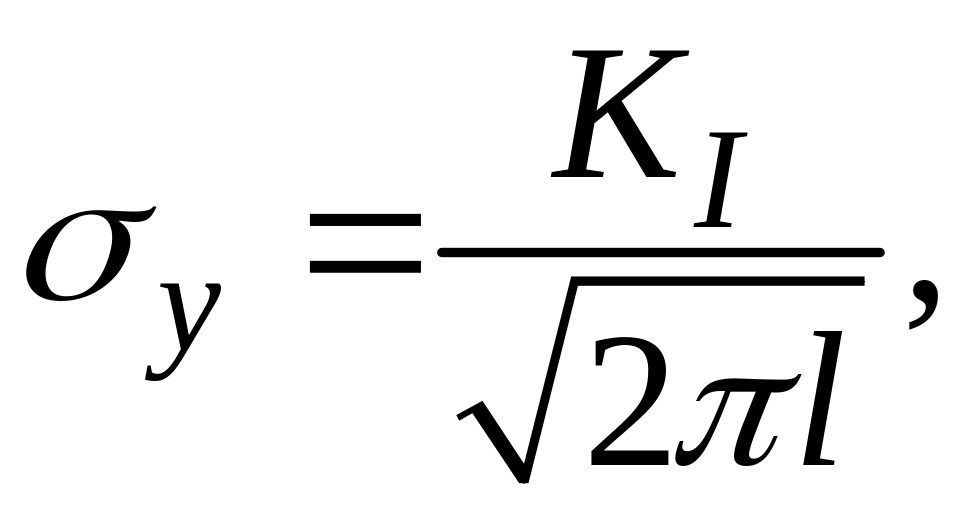то силовой критерий в случае растяжения пластины

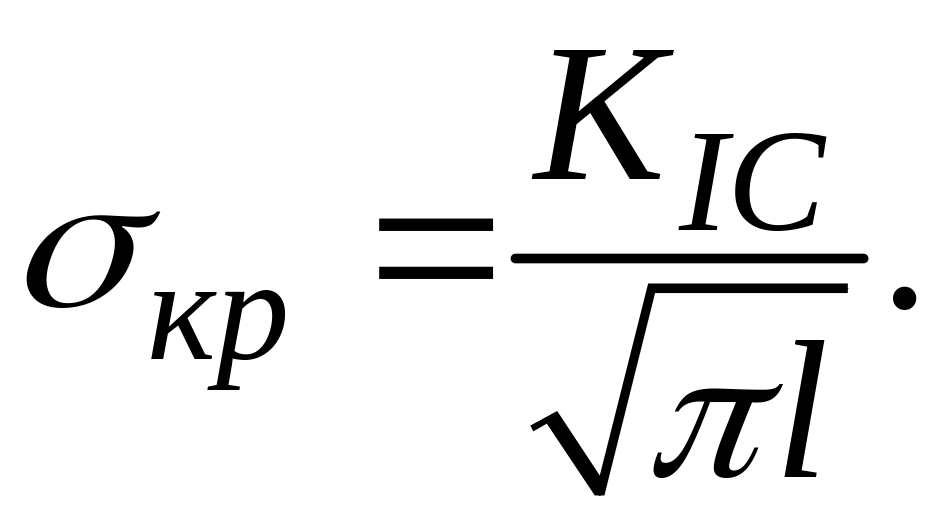
Кривая критического разрушения .

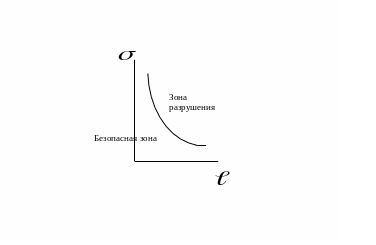
Рис. 29. Кривая разрушения, связывает приложенное напряжение и допустимую длину трещины

4. Схема расчета на трещиностойкость

Цель расчета на трещиностойкость – построение кривой критического разрушения:

а) определяем тип пластины (t << l или t >> l), т. е. формулу для . Плоское напряженное состояние или плоское деформируемое состояние;

б) определяем по таблицам для материала пластины;

б1) вычисляем :

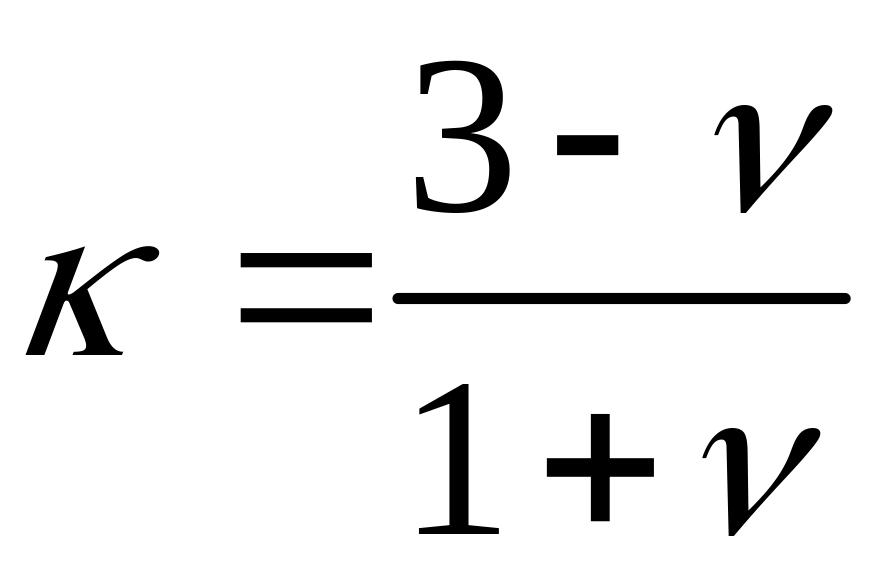– пнс, – пдс;

в) вычисляем

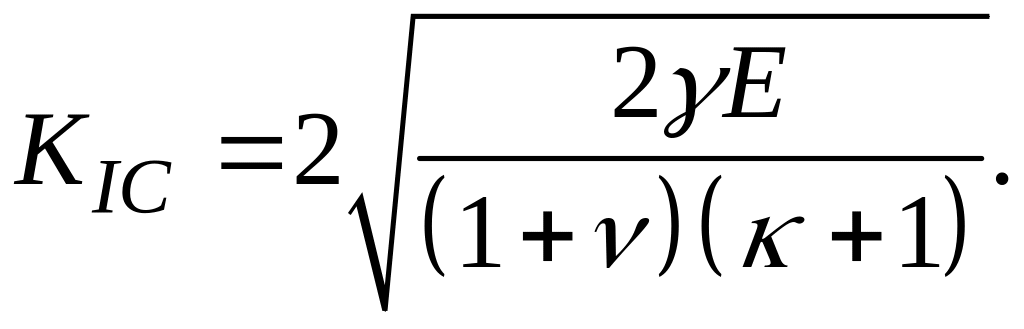
г) по формуле 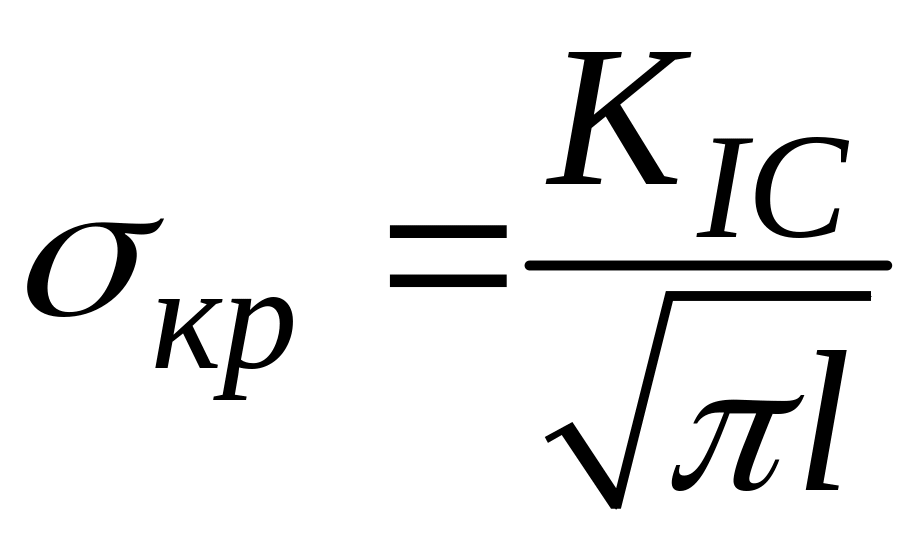строим искомую кривую. Результат – кривая критического разрушения, определение безопасной зоны.

5. Учет пластической зоны

Все рассуждения выше относятся к квазихрупкому разрушению, когда .

Но реально всегда есть расстояние rT, на котором – предел текучести. Это пластическая зона. Найдем rT при

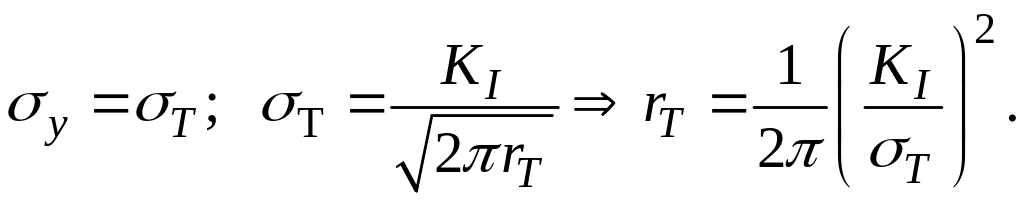
Поскольку для бесконечной пластины, то найдем

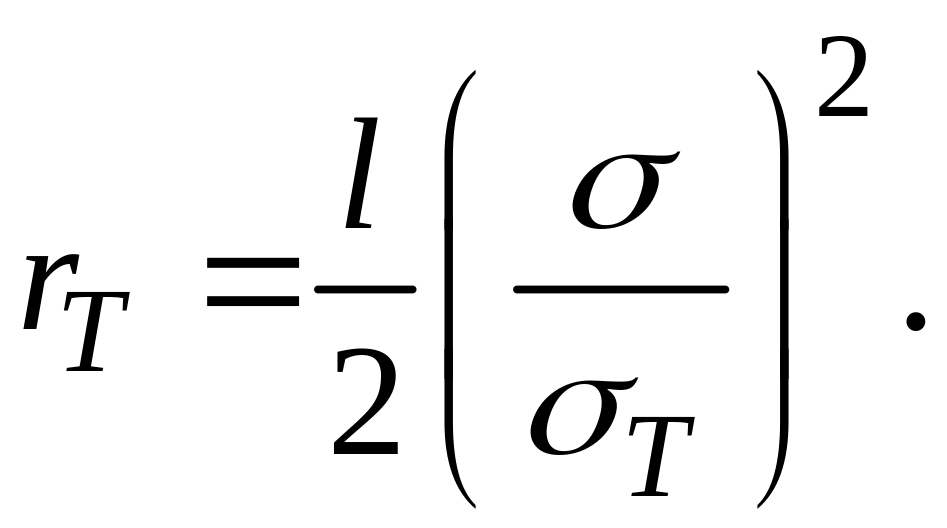
Определим эффективную длину трещины:

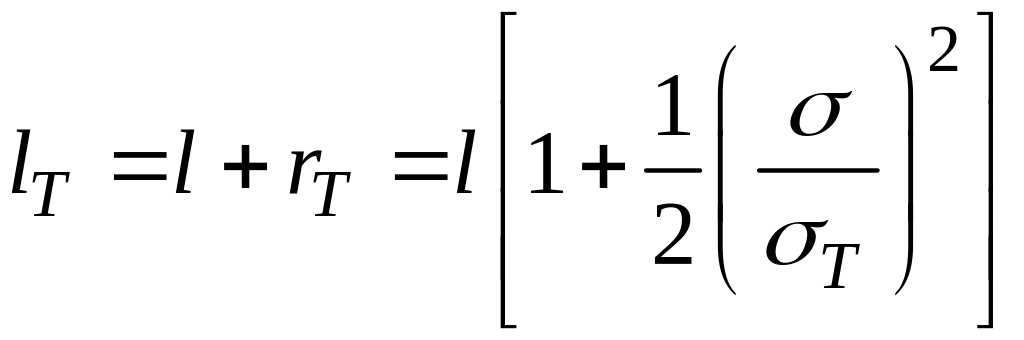
Уточним значение коэффициента интенсивности напряжений:

Поскольку rT зависит от KI, имеем неявную формулу

Это уравнение можно решить численно методом Ньютона относительно .

6. Учет конечности размеров пластины

Обычно пишут , где fI – поправочный коэффициент. Ниже рассмотрены случаи различных трещин и приведен поправочный коэффициент .

А. Наклонная трещина

, – угол наклона трещины.

Б. Односторонняя трещина

В. Пластина шириной 2В с поперечной трещиной посередине:

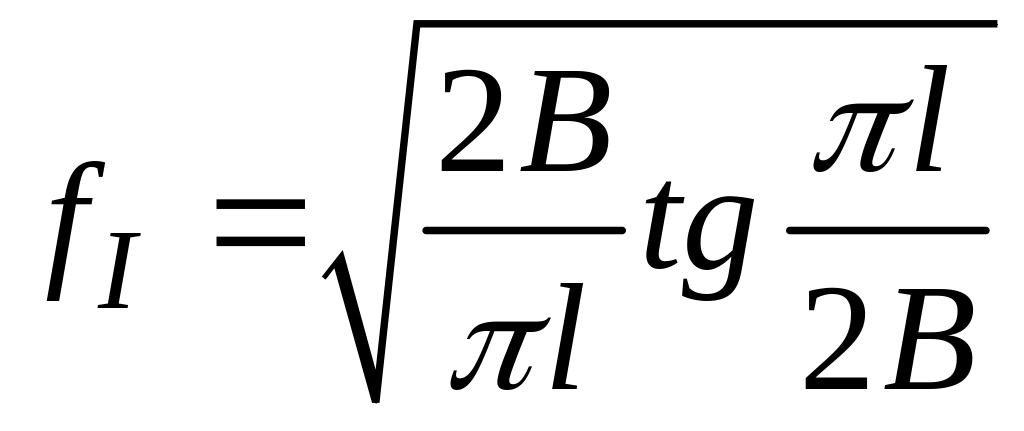
Г. Цилиндрическая труба диаметром 2R и толщиной H под внутренним давлением p при продольной трещине.

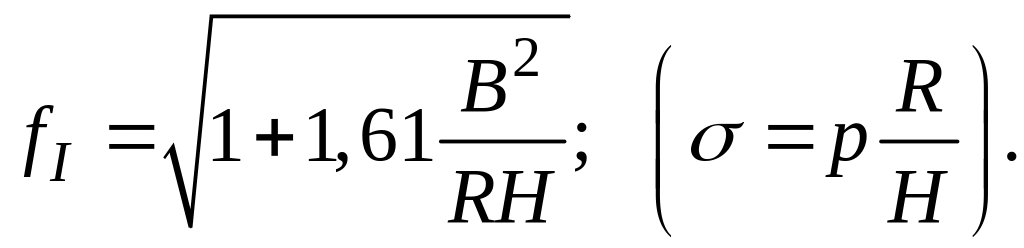
Другие виды трещин – в справочнике [3]. Формула для K_I с учетом пластической зоны:

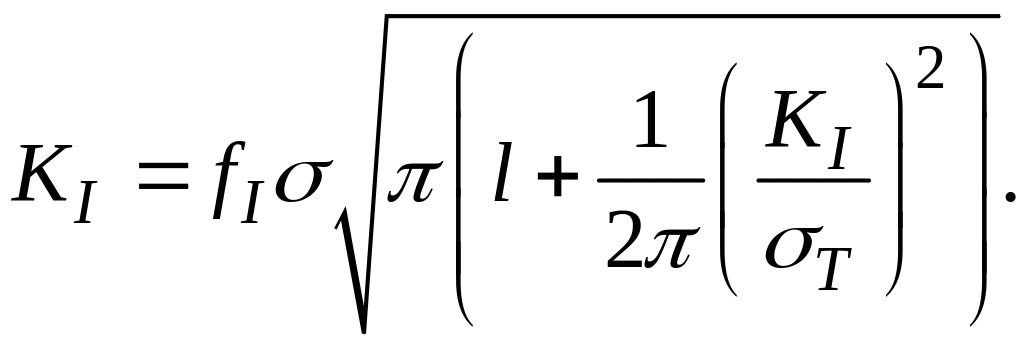
Напомним, что критический коэффициент интенсивности напряжения является константой материала:

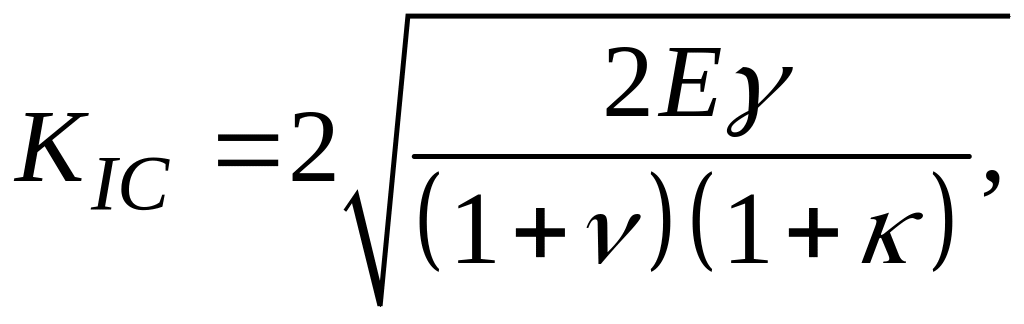силовой критерии разрыва

7. Экспериментальное определение коэффициента интенсивности напряжений

Рассмотрим следующую схему нагружения:

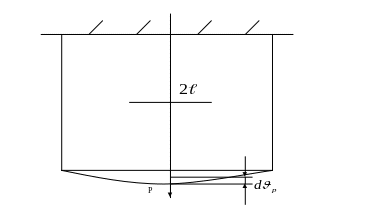
Рис. 30. Эксперимент с подращиваемой трещиной.

Точка приложения силы Р может свободно перемещаться. При продвижении трещины на dl меняется не только энергия деформации пластины dU, но и потенциал внешних сил П, что вызвано перемещением точки приложения Р.

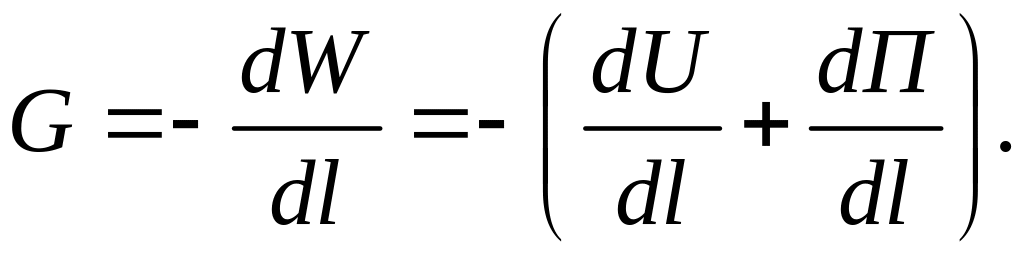
Пусть при Р = 1 перемещение (податливость точки приложения Р). Тогда – по определению (закон сохранения энергии). Коэффициент возник из-за рассмотрения половины трещины. Изменение потенциала внешних сил . Отсюда следует

Теперь можно сформулировать метод определения коэффициента интенсивности напряжений.

А. Численно (методом конечных элементов для задачи теории упругости в перемещениях) или экспериментально (на образце с подращиваемой трещиной) строится зависимость .

Б. Находим численно , откуда

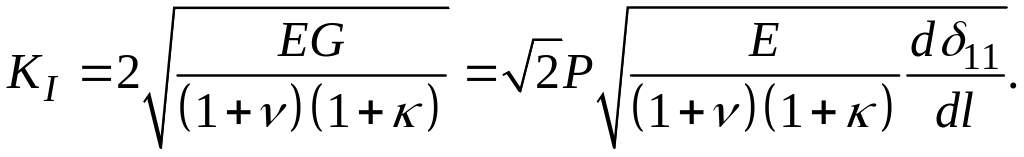
Таким образом, на основании найденного экспериментально коэффициента интенсивности напряжений можно судить о трещиностойкости модельного образца.