
- •Пензенский Государственный Университет Кафедра «Автоматика и телемеханика»
- •Электростатика.
- •1.Электростатическое поле
- •1.1.Электрическое поле в вакууме
- •1.2.Закон Кулона
- •1.3Напряженность Электростатического поля
- •1.4.Принцип суперпозиции
- •1.5.Линии напряженности полей.
- •2.Теорема Остроградского-Гаусса.
- •2.1.Поток векторов напряженности электростатического поля
- •2.2.Теорема Остроградского-Гаусса.
- •2.3.Вектор электрической индукции
- •2.4.Поток электрической индукции
- •2.5.Вывод теоремы Остроградского–Гаусса
- •2.6.Применение теоремы Гаусса
- •3.Электростатическое поле в диэлектрической среде.
- •3.1. Электрический Диполь
- •3.2.Поляризация диэлектриков.
- •4.Постоянный электрический ток
- •4.1.Электрический ток.
- •4.2.Основы классической электрической теории электропроводности металлов.
- •4.3. Закон Ома для плотности тока
- •5.Законы постоянного тока
- •5.1. Закон Ома для неоднородного участка цепи.
- •5.2.Закон Джоуля-Ленца.
- •Магнетизм
- •1.1.Магнитное поле и его свойства
- •1.2.Закон Био-Свара-Лапласа
4.3. Закон Ома для плотности тока
Плотность тока проводимости равна произведению удельной электрической проницаемости на напряженность электрического поля в проводнике.
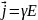
5.Законы постоянного тока
5.1. Закон Ома для неоднородного участка цепи.
На
неоднородном участке цепи на носители
тока действует электростатические силы
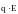 и сторонние силы
и сторонние силы
 .
Следовательно, плотность тока
в этих точках оказывается пропорциональной
сумме напряжений:
.
Следовательно, плотность тока
в этих точках оказывается пропорциональной
сумме напряжений:
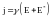 (41)
(41)
Выражение (41) представляет собой закон Ома для неоднородного участка цепи в дифференциальном виде.
Перейдём к интегральной форме закона Ома. Рассмотрим неоднородный участок цепи. В следствие закона сохранения электрического заряда, сила тока в любом сечении проводника будет постоянной.
(Рисунок)
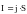
Подставим
в (41) значения
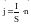 и
и
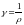 .
Получим выражение для элементарного
участка цепи:
.
Получим выражение для элементарного
участка цепи:

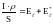 ,
,
где
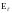 и
и
 - проекции на элемент контура
- проекции на элемент контура
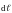 .
.
Умножим последнее соотношение на модуль и проинтегрируем по контуру:
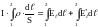 .
.
Учитывая,
что
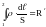 - сопротивление участка цепи 1-2,
- сопротивление участка цепи 1-2,
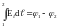 ,
,
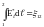 , получим:
, получим:
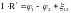 .
.
Если
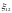 - способствует движению положительных
зарядов в выбранном направлении, то
- способствует движению положительных
зарядов в выбранном направлении, то
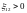 .
.
Если
нет, то
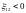 .
.
Запишем последнее соотношение в виде:
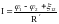 (42)
(42)
(42) представляет собой закон Ома для неоднородного участка цепи в интегральной форме.
Для
замкнутой цепи
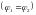 :
:
(Рисунок)
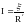 ( 43)
( 43)
Это закон Ома для замкнутого неоднородного у4частка цепи в интегральной форме.
Здесь
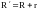 ,
где R
– внешнее сопротивление цепи,
,
где R
– внешнее сопротивление цепи,
 - сопротивление источника ЭДС.
- сопротивление источника ЭДС.
5.2.Закон Джоуля-Ленца.
Если проводник неподвижен и в нём не протекают химические реакции, то работа тока идёт на увеличение внутренней энергии проводника, в результате чего проводник нагревается.
Количество тепла определяется по формуле:
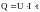 ,
где
,
где
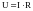
Отсюда:
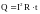 (47)
(47)
Это закон Джоуля-Ленца в интегральной форме.
Если сила тока изменяется во времени, то количество тепла определяется по формуле:
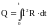 (48)
(48)
Используя закон Джоуля-Ленца можно перейти к выражению, характеризующему выделение тепла в различных физически элементарных объёмах проводника.
Выделив в проводнике элементарный объём в виде цилиндра:
(Рисунок)
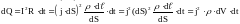
Здесь
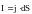 ,
,
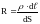 ,
,
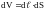
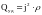
Разделив
полученное уравнение на
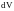 и
и
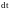 ,
получим формулу удельной тепловой
мощности электрического тока:
,
получим формулу удельной тепловой
мощности электрического тока:
(49)
Обе полученные формулы закона Джоуля-Ленца справедливы и для неоднородного участка цепи, если сторонние силы имеют не химическое происхождение.
Магнетизм
1.1.Магнитное поле и его свойства
Магнитное поле представляет собой особую форму материи и проявляется в пространстве в виде определенного рода сил, которые легко обнаруживаются по своему действию на намагниченные тела. Действие этих сил на намагниченные тела объясняется наличием в телах быстро движущихся внутримолекулярных электрических зарядов
Согласно определению, магнитная индукция и магнитный поток связаны соотношением
![]()
Для характеристики намагниченности вещества в магнитном поле используется магнитный момент рm, который численно равен механическому моменту, испытываемому веществом в магнитном поле с индукцией в 1 Тл
Магнитный момент можно определить из уравнения
![]()
где М - механический момент, испытываемый веществом; α - угол между вектором индукции и вектором магнитного момента.
Магнитный момент единицы объема вещества определяет интенсивность его намагничивания или намагниченность I
![]()
где V - объем вещества.
Магнитное поле характеризуется напряженностью H. Напряженностью магнитного поля в данной точке называется сила, с которой поле действует на единицу положительной магнитной массы, помещенную в эту точку поля.
![]()
Магнитная индукция В связана с напряженностью магнитного поля соотношением
![]()
где μ - относительная магнитная проницаемость среды; μ0 - магнитная постоянная.
Неоднородность магнитного поля в данной его точке характеризуется градиентом его напряженности grad H:
![]()
Для однородных полей dH/dx=0, для неоднородных dH/dx>0. Силой магнитного поля Fп(А2/м3) в данной его точке называют произведение градиента его напряженности на напряженность поля в данной точке
![]()
Магнитные свойства вещества характеризуются магнитной восприимчивостью х и удельной магнитной восприимчивостью
![]()
где δ - плотность вещества.
Магнитная
сила ![]() м,
действующая на минеральное зерно с
массой т, помещенное в магнитное поле,
оценивается зависимостью
м,
действующая на минеральное зерно с
массой т, помещенное в магнитное поле,
оценивается зависимостью
![]()
где
удельная магнитная сила ![]()
Одно из важнейших свойств магнитного поля - явление электромагнитной индукции. Его суть состоит в том, что при всяком изменении магнитного потока, пронизывающего какой-либо контур, в нем наводится электродвижущая сила. Другим свойством магнитного поля является механическое взаимодействие его с электрическим током. Минеральные частицы, попадая в магнитное поле, влияют на расположение его силовых линий. Магнитные частицы оказывают небольшое сопротивление магнитным силовым линиям, поэтому последние в них концентрируются. Устремляясь по кратчайшему пути, силовые линии втягивают магнитные частицы в пространство между полюсами. Немагнитные частицы ухудшают проводимость, поэтому силовые линии обходят их и выталкивают из поля.
Физическая сущность магнитной сепарации состоит в том, что магнитное поле искажает гравитационную траекторию минералов, обладающих соответствующими магнитными свойствами, чем вызывает их извлечение из потока других минералов, которые таких свойств не имеют.
